
リード線のインダクタンス (直線導体/導線)
目的
周波数がある程度高い場合や過渡応答を扱うときに、リード線のインダクタンス成分が影響する場合があります。
リード線のインダクタンスは実際にどれくらいとなるのでしょうか?
参考1のサイト(ページ下部)では、次の式で紹介されています。
※ただし、半径$${a \ \text{[cm]}}$$, 長さ$${l \ \text{[cm]}}$$
(リード線のインダクタンスの式)
$$
L=2l \left( \ln \left( \frac{2l}{a} \right)-1 \right) \quad \text{[nH]}
$$
ここで、
そもそもリード線のインダクタンスとは何なのか?なぜ生じるのか?
なぜリード線のインダクタンスは上式となるのか?
と疑問に思いましたので、本記事に導出過程をまとめました。
本記事の内容を、PDFファイルにまとめました。
リード線のインダクタンスの理論式
リード線のインダクタンスは、半径 $${a [\rm{cm}]}$$ と長さ $${l [\rm{cm}]}$$ から、以下の理論式より概算することができる。
(低周波域におけるリード線のインダクタンス)
$$
L=2l \left( \ln \left( \frac{2l}{a}\right)-\frac{3}{4} \right) \quad \text{[nH]}
$$
ただし、高周波領域では表皮効果により電流が導体表面に集中し、中心部は電流が流れにくくなることから、導体内部のインダクタンスは 0 に近づくため、導体外部のインダクタンス成分が主となり、以下の式となる。
(高周波におけるリード線のインダクタンス)
$$
L=2l \left( \ln \left( \frac{2l}{a}\right)-1 \right) \quad \text{[nH]}
$$
例えば、直径が$${0.5\rm{mm}}$$, 長さ$${2\rm{cm}}$$のリード線は、およそ$${16\rm{nH}}$$のインダクタンス成分が生じる。$${100\rm{MHz}}$$においては、リード線のインピーダンスは$${j10}$$ [Ω]と計算される。
つまり、高周波になるにつれて、リード線のインダクタンスは無視できなくなることが分かる。
また、長さが長いほどインダクタンスが大きくなるため、高周波を扱う場合には、リード(やパターン長)が短ければ短いほど、インピーダンスによる影響が小さいことが上式から分かる。
なぜ?リード線にインダクタンス?
そもそも、なぜリード線にはインダクタンス成分が含まれてしまうのだろうか?
それは自分自身が作りだす磁場によって、誘導起電力が発生してしまうからである。リード線に電流が流れると下図のように回転する磁場が生じる。

これは、アンペールの法則によるものである。
アンペールの法則は以下の式で表される。
$$
\nabla\times\bm{H}=\bm{i}
$$
ここで電流が時間変化する場合を考える。
電流が時間変化するとき磁場も変化する。その時間変化した磁場によりリード線自身に電磁誘導が起こり(自己誘導という)、自己誘導によって磁場の増加を打ち消すような方向に自己誘導起電力が発生する。すなわち、
電流の変化 → 磁場の変化 → 電磁誘導 → 逆起電力
の流れで自己誘導が発生する。
回路の電流変化によって自分自身に生じる起電力の大きさを表す量を自己インダクタンス $${L}$$ という。誘導起電力$${E}$$ は磁束数$${\phi}$$(曲面を通り抜ける磁場の流束)の時間変化でもあるから、以下の式で表される。
$$
\begin{align*}
& E=-\frac{d\mathnormal{\Phi}}{dt}=-L\frac{dI}{dt} \\ \quad \\
& \rightarrow \qquad L=\frac{\mathnormal{\Phi}}{I}
\end{align*}
$$
導出方法
リード線(以下、直線導体という)には、直線導体の内側と外側に自己インダクタンスが発生する。
直線導体内部のインダクタンスを $${L_{i}}$$ , 外部のインダクタンスを $${L_{o}}$$ とすると、導体全体の自己インダクタンスはそれらを足し合わせたものとなる。
$$
L=L_i+L_o
$$
それぞれのインダクタンスを導出し、最終的に冒頭の式が導出できることを示していく。
直線導体内部のインダクタンス
任意の半径 $${r}$$ の直線導体内部の自己インダクタンスを導出する。
(任意の半径とした理由は、導出されるインダクタンスは半径 $${r}$$ に依存しないため。)
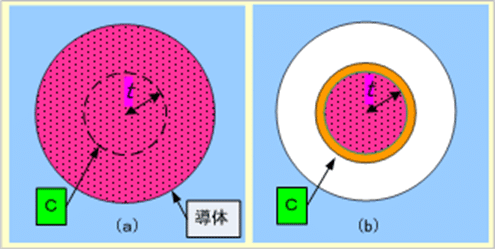
下図のような導体内部を電流 $${i [\rm{A}]}$$ が均等に流れているとき、同図(b)のように導体内の一部 C を流れる電流と、この電流が作る磁束が円筒形導体(茶色部)に同心円状にでき、結果、電流と磁束が鎖交する。これにより、電流が流れる導体内にインダクタンスが生じる。
下図のように、導体(赤色部)の内部で中心Oから $${x [\rm{m}]}$$の部分で、微少厚$${dx [\rm{m}]}$$と紙面と垂直な長さ $${l [\rm{m}]}$$とでつくる断面(緑色部)$${dS}$$(同図(c))を通る磁束の磁束密度を$${B [\rm{T}]}$$、その内部(斜線部)を流れる電流を $${i' [\rm{A}]}$$、導体の透磁率を $${\mu}$$ とし、電流が導体断面を一様に流れているものとするとき、$${i´}$$ による磁束鎖交数 $${d\phi [\rm{Wb}]}$$ を求める。

まず、$${x [\rm{m}]}$$ で囲まれた部分の電流 $${i' [\rm{A}]}$$ は以下の式となる。
$$
i'=\frac{\pi x^2}{\pi r^2}i=\frac{x^2}{r^2}i
$$
次に、中心Oから $${x [\rm{m}]}$$ の部分の電流 $${i' [\rm{A}]}$$ による磁場 $${H [\rm{A/m}]}$$はアンペールの法則より、
$$
\begin{align*}
& \oint_C \bm{H} \cdot d \bm{l}=i' \\ \quad \\
& \rightarrow \qquad H=\frac{x}{2\pi r^2}i
\end{align*}
$$
直線導体の巻き数を考えると、直線導体は半径が無限大の円と考えられることから1巻きのコイルと考えられる。そうした場合、半径$${x}$$における巻き数 $${N’}$$ は以下の式で表される。
$$
N'=\frac{\pi x^2}{\pi r^2} \cdot 1=\frac{x^2}{r^2}
$$
したがって、微小面積$${dS}$$を通る磁束 $${d\phi [\rm{Wb}]}$$ は以下の式となる。
$$
d\mathnormal{\Phi}=N'BdS=\frac{\mu ix^3}{2\pi r^4}dx
$$
導体内部の鎖交磁束は $${\mathnormal \Phi}$$ は $${x : 0 → r}$$ の範囲で積分することで求まる。
$$
\begin{align*}
\mathnormal{\Phi}=\int_{x=0}^{r} d\mathnormal{\Phi} &=\int_{x=0}^{r} {\frac{\mu i x^3}{2 \pi r^4}dx} \\ \quad \\
&=\frac{\mu i}{2\pi r^4} \left[ \frac{1}{4}x^4 \right]_0^r \\ \quad \\
&=\frac{\mu i}{8 \pi}
\end{align*}
$$
したがって、$${l [\rm{m}]}$$ の長さの導体内のインダクタンス $${L_{i} \rm{[H]}}$$ は以下の式となる。下記式の通り、導体内部のインダクタンスは導体の半径に依存しない。
$$
L_i=\frac{\mathnormal{\Phi}}{i}l=\frac{\mu l}{8 \pi} \quad \text{[H]}
$$
直線導体外部のインダクタンス
半径$${a \rm{[m]}}$$の円形断面をもつ直線導体で、長さ$${l \rm{[m]}}$$部分の導体外の自己インダクタンス $${L_{o} \rm{[H]}}$$ を求める。

まずは、導体中心をXY座標のY軸に合わせ、その端が原点となるように置く。この導体がつくる磁界中(青色部)の点P $${(x, y)}$$ $${(x : a→ ∞, y : 0 → l )}$$に、導体の微少長(赤色部)$${dl \rm{[m]}}$$に電流 $${i \rm{[A]}}$$が流れるためにつくられる磁界$${dH}$$は、ビオ・サバールの法則より以下の式の通り計算される。
$$
\begin{align*}
d \bm{H} &=\frac{i}{4\pi r^3}d\bm{l}\times\bm{r} \\ \quad \\
\lvert d\bm{H} \rvert &=\frac{i}{4\pi r^3}dl \ r \ \sin(90\degree -\theta) \\ \quad \\
&=\frac{i}{4\pi r^2}dl \ \cos\theta
\end{align*}
$$
ここで図(b)のような半径 $${r}$$ の円弧を考えると、微小導体による磁界 $${dH}$$ は以下の式となる。
$$
\begin{align*}
\lvert d\bm{H}\rvert =dH &=\frac{i}{4\pi r}d\theta \\ \quad \\
&=\frac{i}{4\pi x} \cos\theta \ d\theta \\ \quad \\
\end{align*}
$$
$${dl\cos\theta=r d\theta}$$となる理由は下図参照。
※別サイトからの引用のため代数の置き方が異なることに注意。

したがって、長さ $${l \rm{[m]}}$$の導体による磁界 $${H \rm{[A/m]}}$$ は次式となる。
$$
\begin{align*}
H&=\int_{-\alpha_1}^{\alpha_2}{\frac{i}{4\pi x}\cos\theta \ d\theta} \\ \quad \\ &=\frac{i}{4\pi x}(\sin\alpha_1+\sin\alpha_2) \\ \quad \\
&= \frac{i}{4\pi x} \left( \frac{l-y}{\sqrt{x^2+(l-y)^2}}+\frac{y}{\sqrt{x^2+y^2}} \right)
\end{align*}
$$
導体外の閉曲面$${(x : a→ ∞, y : 0 → l )}$$と鎖交する磁束$${\mathnormal\Phi}$$ は次式となる。
(鎖交磁束はコイルを貫く磁束であるが、今回のケースの直線導体の場合、復路の電流が流れる導線が、無限に離れた場所にあると考えると分かりやすい。)
$$
\mathnormal{\Phi}=\int{\bm{B}\cdot\bm{n} \ dS}=\mu_0\int{\bm{H}\cdot\bm{n} \ dS}
$$
磁界 $${\bm H}$$ の向きは、閉曲面に対し垂直であることから、磁束$${\mathnormal\Phi}$$ は次の式の通り展開できる。
※ 式内の $${x}$$ 積分はAppendix を参照のこと。
$$
\begin{align*}
\mathnormal{\Phi}&=\frac{\mu_0 i}{4\pi}\int_{x=a}^{x=\infin}{\frac{1}{x} \left\{ \int_{y=0}^{y=l}{\left( \frac{l-y}{\sqrt{x^2+(l-y)^2}}+\frac{y}{\sqrt{x^2+y^2}} \right) dy} \right\} dx } \\ \quad \\
&=\frac{\mu_0 i}{4\pi}\int_{x=a}^{x=\infin}{\frac{1}{x} \left\{ \left[ -\sqrt{x^2+(l-y)^2}+\sqrt{x^2+y^2} \right]_{y=0}^{y=l} \right\} dx} \\ \quad \\
&=\frac{\mu_0 i}{2\pi} \int_{x=a}^{x=\infin}{ \left( \frac{\sqrt{x^2+l^2}}{x}-1\right)dx} \\ \quad \\
&=\frac{\mu_0 i}{2\pi} \left( l \ln{\frac{l+\sqrt{a^2+l^2}}{a}-\sqrt{a^2+l^2}+a} \right)
\end{align*}
$$
したがって、導体外の自己インダクタンス $${L_{o}}$$ は以下の式となる。
$$
L_o=\frac{\mathnormal{\Phi}}{i}=\frac{\mu_0}{2\pi}\left( l \ln{\frac{l+\sqrt{a^2+l^2}}{a}-\sqrt{a^2+l^2}+a} \right)
$$
直線導体のインダクタンス
導体内部/外部の自己インダクタンス$${L_{i} \rm{[H]}, \mathnormal L_{o} \rm{[H]} }$$はそれぞれ、以下の通り求まった。
$$
\begin{dcases} L_i=\frac{\mu l}{8\pi} \\ \quad \\ L_o=\frac{\mu_0}{2\pi}\left( l \ln{\frac{l+\sqrt{a^2+l^2}}{a}-\sqrt{a^2+l^2}+a} \right) \end{dcases}
$$
まず、外部インダクタンスを考える。導体の長さ$${l \rm{[m]}}$$ が半径$${a \rm{[m]}}$$に対し十分に長い時、以下の式のように近似できる。
$$
L_o \fallingdotseq \frac{\mu_0 l}{2\pi}\left( \ln{\frac{2l}{a}-1} \right)
$$
真空の透磁率 $${\mu_{0}=4 \pi \times10^{-7}}$$であることから、$${a \rm{[cm]}, \mathnormal l \rm{[cm]}}$$ と単位を変えると、$${L_{o} \rm{[nH]}}$$ は、冒頭の式の通り変形できる。
$$
L_o \fallingdotseq 2l \left( \ln{\frac{2l}{a}-1} \right) \quad\text{[nH]}
$$
次に、内部インダクタンスの式の透磁率は、銅やアルミの比透磁率がほぼ $${1}$$ であることから、真空の透磁率とほぼ等価であるため、以下の式の通り近似できる。
$$
L_i=\frac{\mu_0 l}{8\pi}
$$
したがって、直線導体のインダクタンスは、$${L_{i} \rm{[nH]}, \mathnormal L_{o} \rm{[nH]} }$$を足し合わせた以下の式となる。
$$
\begin{align*}
L&=2l \left(\ln \left(\frac{2l}{a} \right)-\frac{3}{4} \right) \quad \text{[nH]} \\ \quad \\
&\text{※ただし、半径} a \ \text{[cm], 長さ} l \ \text{[cm]}
\end{align*}
$$
ただし、高周波領域では表皮効果により電流が導体表面に集中し、中心部は電流が流れにくくなることから、導体内部のインダクタンスは$${0}$$ に近づくため、導体外部のインダクタンス成分が主となり、以下の式となる。
$$
\begin{align*}
L \fallingdotseq L_o=2l \left( \ln{\frac{2l}{a}-1} \right) \quad\text{[nH]}& \\ \quad \\
\text{※高周波領域}&
\end{align*}
$$
(Appendix)磁束Φ 導出過程のx積分
以下の式の計算方法を記述する。
$$
\int_{x=a}^{x=\infin} {\left( \frac{\sqrt{x^2+l^2}}{x}-1 \right)dx}
$$
$${t=\sqrt{x^2+l^2}}$$ に置換すると、
$$
\begin{align*}
\frac{dt}{dx}&=\frac{x}{\sqrt{x^2+l^2}} \\ \quad \\
\rightarrow \ \qquad t \ dt&=x \ dx
\end{align*}
$$
積分内の第 1 項を変形すると、
$$
\begin{align*}
\frac{\sqrt{x^2+l^2}}{x}dx&=\frac{t}{x}\cdot\frac{t}{x}dt \\ \quad \\
&=\frac{t^2}{t^2-l^2}dt \\ \quad \\
&= \left\{ 1+\frac{l}{2} \left( \frac{1}{t-l}-\frac{1}{t+l} \right) \right\}dt
\end{align*}
$$
したがって、積分を展開すると、
$$
\begin{align*}
\int_{x=a}^{x=\infin}& {\left( \frac{\sqrt{x^2+l^2}}{x}-1 \right)dx} \\ \quad \\
&=\int_{t=\sqrt{a^2+l^2}}^{t=\infin} {\left\{ 1+\frac{l}{2}\left( \frac{1}{t-l}-\frac{1}{t+l} \right) \right\}dt}-\int_{x=a}^{x=\infin}{dx} \\ \quad \\
&=\left[ t+\frac{l}{2}\ln{\frac{t-l}{t+l}}\right]_{\sqrt{a^2+l^2}}^{\infin} - [x]_a^\infin \\ \quad \\
&=t\vert_\infin-x\vert_\infin-\sqrt{a^2+l^2}-a-\frac{l}{2}\ln\frac{\sqrt{a^2+l^2}-l}{\sqrt{a^2+l^2}+l} \\ \quad \\
&=\frac{l}{2}\ln\frac{\sqrt{a^2+l^2}+l}{\sqrt{a^2+l^2}-l}-\sqrt{a^2+l^2}-a
\end{align*}
$$
ここで、$${\tan\theta=a/l}$$とすると、
$$
\begin{align*}
\frac{l}{2}\ln{\frac{\sqrt{a^2+l^2}+l}{\sqrt{a^2+l^2}-l}}&=\frac{l}{2}\ln{\frac{1+\cos\theta}{1-\cos\theta}} \\ \quad \\
&=\frac{l}{2}\ln{\frac{(1+\cos\theta)^2}{1-\cos^2\theta}} \\ \quad \\
&=l\ln{\frac{1+\cos\theta}{\sin\theta}} \\ \quad \\
&=l\ln{\frac{\sqrt{a^2+l^2}+l}{a}}
\end{align*}
$$
最終的に、以下の式が導出される。
$$
\int_{x=a}^{x=\infin} {\left( \frac{\sqrt{x^2+l^2}}{x}-1 \right)dx}=l\ln{\frac{\sqrt{a^2+l^2}+l}{a}}-\sqrt{a^2+l^2}-a
$$
参考文献
参考1 electronics notes ~ Inductance of Straight Wire & Coils ~
参考2 インダクタンスの求め方
参考3 有限長直線導体による磁界
この記事が気に入ったらサポートをしてみませんか?
