平行2線式線路のインダクタンス

2023年7月18日 12:59

本稿では、平行2線式線路のインダクタンスの式と導出方法を紹介する。

インダクタンスの式

下図のように平行する線路が無限長の長さを持つとき、線の半径を$${a \ [\text m]}$$および線間距離を$${d \ [\text m]}$$とすると、単位長さ当たりの平行2線式線路がもつインダクタンス$${L \ \text{[H/m]}}$$は、次式となる。

$$
L=\frac{\mu_0}{\pi}\ln\frac{d-r}{r} \quad \text{[H/m]}
$$

導出方法

インダクタンス$${L \ [\text{H}]}$$は、コイルを流れる電流が$${I\ [\text{A}]}$$であるとき、コイルの巻き線を貫く鎖交磁束が$${\psi \ [\text{Wb}]}$$であったときの比例係数である。
（$${n}$$はコイルの巻き数）

$$
L=\frac{n \psi}{I} \quad \text{[H]}
$$

コイルを流れる電流が時間変化すると電磁誘導により磁場が発生し、さらにその磁場がコイルに起電力$${V}$$を誘導する。その関係は次式となる。

$$
V = L\frac{\text{d}I}{\text{d}t} \quad \text{[V]}
$$

ここで、平行2線式線路における鎖交磁束とは何かを考える。
下図の通り、平行2線式線路を十分に遠いところから見ると、一巻きのコイルとみなせる。したがって、鎖交磁束はそのコイルを貫く磁束であり、単位長さ当たりインダクタンスは単位長さの2線の導体に囲まれた面積を貫く鎖交磁束から求まる。

以上を踏まえて、インダクタンスを以下の流れで導出していく。

磁界の強さ$${H \ [\text{A/m}]}$$の導出
鎖交磁束$${\psi \ [\text{Wb}]}$$の導出
インダクタンス$${L \ [\text{H}]}$$の導出

(STEP 1) 磁界の強さの導出

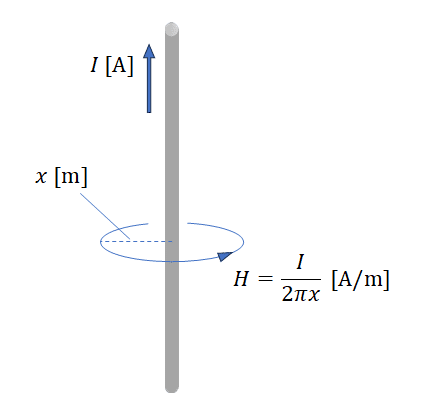
直線導体に電流$${I \ \text{[A]}}$$が流れているとき、導体中心から距離$${x\ \text{[m]}}$$離れた点に生じる磁界の強さ$${H \ \text{[A/m]}}$$は次式となる。

$$
H=\frac{I}{2\pi x} \quad \text{[A/m]}
$$

平行2線式線路では、電流の向きが対向しているため、下図の上側導体Aと下側導体Bに囲まれた平面を貫く磁界の向きは同じ向きとなる。
上式より上側導体Aの中心から距離$${x \ [\text{m}]}$$離れた点に生じる磁界の強さは下式となる。

$$
H=\frac{I}{2\pi x}+\frac{I}{2\pi (d-x)} \quad \text{[A/m]}
$$

第1項は導体Aが作る磁界、第2項は導体Bが作る磁界である。

(STEP 2) 鎖交磁束の導出

磁界の強さ$${H \ [\text{A/m]}}$$より、磁束密度$${B \ [\text{Wb/m}^2]}$$は真空の透磁率$${\mu_0}$$を用いて次式となる。

$$
B=\mu_0H= \frac{\mu_0I}{2\pi x}+\frac{\mu_0I}{2\pi (d-x)} \quad [\text{Wb/m}^2]
$$

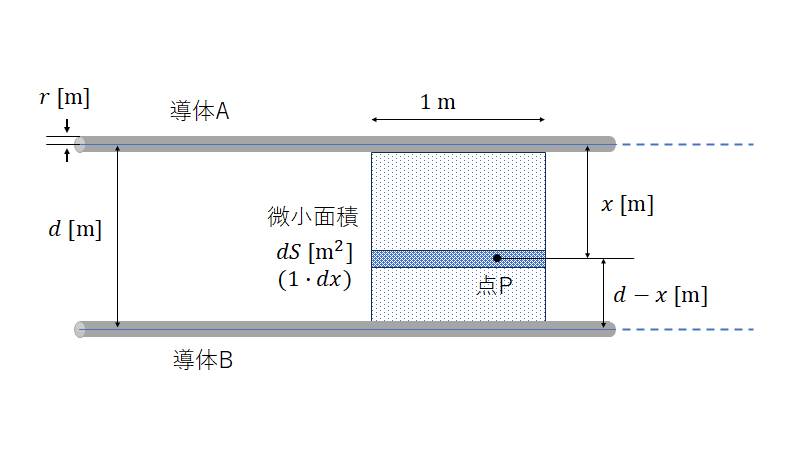
鎖交磁束$${\psi\ [\text{Wb}]}$$は導体Aと導体Bに囲まれた平面の内、単位長さの区間の平面を貫く磁束密度を面積分することで導出される。

導体Aから距離$${x \ [\text m]}$$離れた点Pにおける微小幅$${dx}$$と長さ$${1 \ \text m}$$に囲まれた微小面積$${dS}$$を貫く鎖交磁束$${d\psi}$$は次式となる。

$$
\begin{align*}
d\psi&=BdS \\ \quad \\
&=\left( \frac{\mu_0I}{2\pi x}+\frac{\mu_0I}{2\pi (d-x)} \right) \ dx \\ \quad \\
&=\frac{\mu_0I}{2\pi} \left( \frac{1}{x}+\frac{1}{d-x} \right) dx
\end{align*}
$$

微小幅における鎖交磁束$${d\psi}$$を$${x: r \rightarrow d-r}$$の区間で積分することで鎖交磁束$${\psi}$$を求めることができ、次式の通り導出される。

$$
\begin{align*}
\psi &= \int_{r}^{d-r}{d\psi} \\ \quad \\
&=\frac{\mu_0I}{2\pi} \int_{r}^{d-r}{\left( \frac{1}{x}+\frac{1}{d-x} \right) dx} \\ \quad \\
&=\frac{\mu_0I}{2\pi} \left[ \ln{x-\ln{(d-x)}}\right]_r^{d-r} \\ \quad \\
&=\frac{\mu_0I}{2\pi}\left( \ln{(d-r)} - \ln{r}\right) -\left( \ln{r} - \ln{(d-r)}\right) \\ \quad \\
&= \frac{\mu_0I}{\pi} \ln{\frac{d-r}{r}}
\end{align*}
$$

(STEP 3) インダクタンスの導出

STEP2で、単位長さの導体A, Bに囲まれた面積における鎖交磁束$${\psi \ [\text{Wb}]}$$は次式の通り導出された。

$$
\psi = \frac{\mu_0I}{\pi} \ln{\frac{d-r}{r}} \quad [\text{Wb}]
$$

また、インダクタンスと鎖交磁束の関係式は次式の通り。
（巻き数は$${n=1}$$）

$$
L=\frac{\psi}{I} \quad \text{[H]}
$$

したがって、無限長の平行2線式線路の単位長さ当たりのインダクタンスは、次式の通り導出される。

$$
L = \frac{\mu_0}{\pi} \ln{\frac{d-r}{r}} \quad [\text{H/m}]
$$

まとめ

平行2線式線路の単位長さ当たりのインダクタンスは以下の式で導出された。

$$
L = \frac{\mu_0}{\pi} \ln{\frac{d-r}{r}} \quad [\text{H/m}]
$$

ただし、$${d>>r}$$の場合、次式の通り近似できる。

$$
L \simeq \frac{\mu_0}{\pi} \ln{\frac{d}{r}} \quad [\text{H/m}]
$$

今回の導出では、導体外部のインダクタンスのみ考慮し、導体内部のインダクタンスは無視した。導体内部のインダクタンスについては、下記記事をご参照のこと。ただし、高周波の場合、電流は導体表面に集中するため、導体内部のインダクタンスは無視できる。

参考文献

この記事が気に入ったらサポートをしてみませんか？