
微小ダイポールアンテナの放射抵抗の式の導出と放射効率について
放射抵抗(radiation resistance)とは、アンテナのインピーダンスの内、アンテナから実際に電磁波として放出される電力に対応する抵抗値のこと。
本稿では、その放射抵抗の概要と、微小ダイポールアンテナの放射抵抗の導出方法および放射効率に関して記述する。
放射抵抗
アンテナは、入力された電力を電磁波に変換して空間に放射する。この放射される電力を放射電力という。
アンテナで電力が消費されるということは、アンテナをインピーダンスとしてみなせるということである。アンテナの給電点からみたインピーダンスの内、放射電力に関わる抵抗成分を放射抵抗と呼ぶ。
アンテナのインピーダンスのモデル例を下記に示す。
アンテナで消費される電力は、「熱損失として消費される電力」と「空間に放射される電力」に分けられる。
熱損失電力が消費される抵抗を$${R_l}$$, 空間に放射される電力が消費される抵抗を$${R_r}$$としている。$${L, C}$$は、アンテナが持つリアクタンス成分である。

放射抵抗は、アンテナの設計や形状に依存し、アンテナが効率的に電磁波を放射する能力を評価する指標となる。放射抵抗が高いほど、アンテナは電磁波を効率的に放射できる。
しかし、放射抵抗が高い場合は、システムインピーダンス(50Ω)とのマッチングが取れなくなってしまうため、整合回路が必要となる。
したがって、アンテナを理想的に動作するためには、マッチングが取れていることと放射効率が高いことの2つが要求される。
※放射効率の章を参照。
放射抵抗は、アンテナが放射する電磁波の総電力とアンテナに流れる電流値から計算される。
例として、微小ダイポールアンテナの放射抵抗は以下の式となる。
$$
R_r = 80\pi^2 \left( \frac{l}{\lambda}\right)^2
$$
放射抵抗の式の導出
本章で、微小ダイポールアンテナの放射抵抗の式を導出していく。
その導出方法を簡単にまとめると、以下の流れとなる。
単位面積を通過する電磁エネルギー密度をポインティング・ベクトルから計算する。→ $${P_u=|\bm{S}|}$$
その電磁エネルギー密度をアンテナを囲む球面に関して面積分することで、放射電力の総和を求める。→ $${\iint_{} P_u\ dS}$$
放射電力の総和と電流から放射抵抗を計算する。→ $${R_r=P/I^2}$$
1. 電磁エネルギー密度を求める
遠方界における微小ダイポールアンテナの電界、磁界の式は下記の通りとなる。
$$
\begin{align*}
E_\theta&=j \frac{IlZ_0k_0}{4\pi r} e^{-jk_0r}\sin \theta \\ \quad \\
H_\phi&=j \frac{Ilk_0}{4\pi r} e^{-jk_0r}\sin \theta \\
\end{align*}
$$
微小ダイポールアンテナの電界/磁界の導出方法は、下記記事を参照のこと。
この電界および磁界の式から単位面積を通過する電磁エネルギー密度$${P_u}$$を求める。
$${P_u}$$はポインティングベクトルの絶対値$${|\bm{S}|}$$と同等となり、以下の式となる。
$$
P_u=|\bm{S}|=|\bm{E}\times\bm{H}|=\frac{{E_\theta}^2}{120\pi}\quad [\text{W/m}^2]
$$
この式の導出は、下記記事の”ポインティングベクトル”の章を参照のこと。
したがって、$${E_\theta}$$を$${P_u}$$に代入すると、放射電力$${P_u}$$は以下の式となる。
$$
P_u=\frac{{E_\theta}^2}{120\pi}=\frac{30\pi I^2 l^2}{\lambda^2 r^2} \sin ^2\theta \quad [\text{W/m}^2] \\ \quad \\
\text{※}k_0=\frac{2\pi}{\lambda},\ Z_0=120\pi
$$
上式から、単位面積あたりを通過する放射電力は電界の2乗で与えられることが分かった。
アンテナの全放射電力は、アンテナを原点とする閉曲面を設定して、単位面積当たりの放射電力$${P_u}$$を面積分することで求まるが、その積分を視覚的にイメージするために、微小ダイポールアンテナによる電磁波がどのように放射されるかをまず理解する。
一般にアンテナには指向性があり、アンテナの放射電力の強さはアンテナからの角度に依存する。その指向性を表したものを放射パターンという。(いくつか方式はあるが、)放射パターンは、最も電界が強くなる角度$${(\theta, \ \phi)}$$を基準(1 もしくは0dB)とした時の、各角度における電界強度をプロットしたものである。
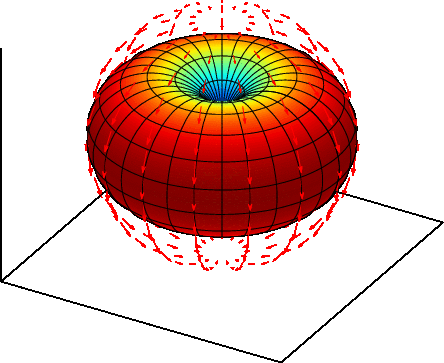
微小ダイポールアンテナの放射パターン(3D表示)を下図に示す。
ダイポールアンテナの放射パターンはドーナッツ型となる。
アンテナを原点にz軸に沿っておいたとき、$${X-Y}$$平面$${(Z=0)}$$における電界強度が最大となる。放射電力$${P_u}$$の式から分かる通り、放射電力は$${\phi}$$方向に依存しない。すなわち無指向性である。
http://www.emlab.cei.uec.ac.jp/denjikai/dipole.html
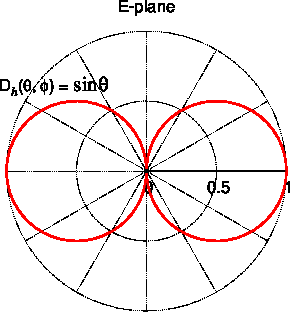
ドーナッツを、z軸を通るように、縦から切ったときの放射パターン(E面)は8の字上となる。電界強度は$${\theta}$$に応じて電界が変化するため、指向性を持つ。
http://www.emlab.cei.uec.ac.jp/denjikai/dipole.html
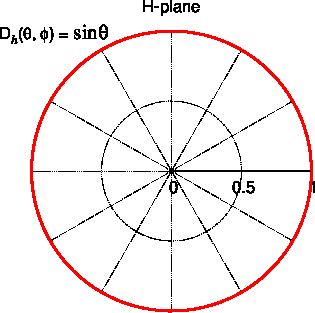
ドーナッツを、z軸から垂直となるように、横から切ったときの放射パターン(H面)は円状となる。すなわち、電界強度は$${\phi}$$によって変化せず、H面は指向性を持たない。
http://www.emlab.cei.uec.ac.jp/denjikai/dipole.html
2. 放射電力の総和を求める
前項にて単位面積を通過する微小ダイポールアンテナによる放射電力$${P_u}$$が求まった。全放射電力は、波源を中心として半径が$${r}$$の球を考え、その閉曲面を通過する電力を積分すれば求まる。
前項で記述した通り、放射電力は$${\phi}$$に依存しないため、下図の赤い部分のように、z軸を中心とする微小な幅$${r\cdot d\theta}$$の円環の曲面を通過する電力$${dP}$$を計算した後、$${\theta=0\rightarrow \pi}$$の区間で積分することで、閉曲面を通過する全放射電力が求まる。

まず、円環の面積$${dS}$$を求める。
円環の幅は、弧度法(ラジアン)の定義より、$${r \cdot d\theta}$$となる。
円環の円周は、図に示された$${x_r}$$となる。
以上から、微小幅円環の面積$${dS}$$は以下の式となる。
$$
dS=(2\pi r \sin\theta)(r d\theta)=2\pi r^2\sin\theta \ d\theta
$$
したがって、円環の曲面を通過する電力$${dP}$$は以下の通り導出される。
$$
\begin{align*}
dP=P_u\ dS &=\left( \frac{30\pi I^2 l^2}{\lambda^2 r^2} \sin^2 \theta\right) \left(2\pi r^2\sin\theta \ d\theta \right) \\ \quad \\
&=\frac{60\pi^2 I^2 l^2}{\lambda^2 } \sin^3 \theta d\theta
\end{align*}
$$
$${dP}$$を$${\theta = 0 \rightarrow \pi}$$の区間で積分することで、全電力$${P}$$が求まる。
まず、$${\sin^3 \theta}$$の$${\theta}$$積分は以下の式で与えられる。
$$
\int_{0}^{\pi}\sin^3\theta \ d\theta=\left[ \frac{1}{3}\cos^3\theta-\cos\theta \right]_{0}^{\pi}=\frac{4}{3}
$$
したがって、球の閉曲面を通過する全電力$${P}$$は、以下の式の通り、求まる。
$$
P=\frac{60\pi^2 I^2 l^2}{\lambda^2 } \int_{0}^{\pi}\sin^3 \theta d\theta=\frac{80\pi^2 I^2 l^2}{\lambda^2 }
$$
3. 放射電力の総和と電流から放射抵抗を計算する
放射抵抗は、放射電力とアンテナを流れる電流値から計算される。
まず、前項にて放射電力の総和$${P}$$は以下の式の通り求まった。
$$
P=\frac{80\pi^2 I^2 l^2}{\lambda^2 }
$$
したがって、$${P=I^2R_r}$$の関係であることから、微小ダイポールアンテナの放射抵抗$${R_r}$$は以下の式の通り導出される。
$$
R_r=\frac{80\pi^2 l^2}{\lambda^2 }
$$
放射効率
アンテナは、下記モデルで示されるように、アンテナの入力電力が全て放射されるわけでなく、アンテナ内で熱に変わる損失電力がある。
アンテナがどれだけ効率よく入力電力$${P}$$を放射電力$${P_r}$$に変換できたかを示す指標を放射効率という。放射効率は$${P_r/P}$$で計算される。

上記モデルの時、放射効率の式は以下の通りとなる。
$$
\eta=\frac{P_r}{P}=\frac{R_r}{R_r+R_l}
$$
上式から分かる通り、放射抵抗が損失抵抗より大きいほど、空間に放射される電力が大きくなる。(効率向上)
下記グラフは、損失抵抗を20Ωとしたときの、放射効率と放射抵抗の関係を表す。
放射抵抗が大きくなるほど、放射効率が上昇していることが読み取れる。

放射効率だけを考えるならば、放射抵抗は高ければ高い方が良い。
しかし、実際の回路ではインピーダンスマッチングを考える必要がある。
アンテナのインピーダンスがシステムインピーダンスと整合が取れていないと、効率的に電力を伝達できない。
下図は、システムインピーダンスを$${50\Omega}$$とした時の、入出力電力と出力抵抗の関係を表す。(入力電圧 = 1Vとする。)
下図の通り、出力抵抗がシステムインピーダンスを一致するときに、出力電力は最大となり、出力電力が入力電力と一致していることが分かる。

これをインピーダンスマッチング(整合)という。
高周波においては、整合が取れていないとき、出力負荷(アンテナ)に伝達できなかった電力は、ノイズとなって入力回路側に反射してしまう。その現象により、不整合時には、意図通りの出力がなされなかったり、信号品質の低下を引き起こしてしまう。
そのため、インピーダンス整合は重要である。
以上より、アンテナを理想的に動作するためには、マッチングが取れていることと放射効率が高いことの2つが要求される。
放射抵抗は高ければ高い方が放射効率は良いが、システム全体の効率を考えると、入力回路側とのインピーダンスマッチングも必要になる。
逆に言うと、整合がとれている(S11が小さい)からと言って効率よく放射されているとは限らない。整合がとれていることは、アンテナが理想的な状態で動作するための必要条件であって十分条件ではない。
参考文献
小形アンテナの特性と設計に使う基本式
http://www.rf-world.jp/bn/RFW14/samples/p018-019.pdf
2章 アンテナの基礎 (電子情報通信学会)
http://ieice-hbkb.org/files/04/04gun_02hen_02.pdf
この記事が気に入ったらサポートをしてみませんか?
