
フォークボールが落ちるワケ:流体解析が説明した「負のマグヌス効果」(思惟かねの科学技術ニュース解説)
先日、面白い科学ニュースが入ってきました。
野球の変化球に関する流体力学的な研究です。野球を知っている人なら、中々気になるニュースだと思います。
ピッチングの基本となる「伸びる」球であるストレートと、変化球の一つ、「落ちる」球のフォークボール。一見すると全く違うように思える両者ですが、実はボールはどちらも同じバックスピンで回転しています。
いったい両者の差はどこから生まれるのか?ということを、相違点となるシーム(球の縫い目の握り方=縫い目に対する回転方向)を考慮した、非常に詳細な数値流体解析(Computer Fluid Dynamics: CFD)によって明らかにした研究です。
今回はこちらのニュースを、もう少し踏み込んで解説してみました。
◆変化球の立役者「マグヌス効果」と「シーム」
地球上では重力があるために、投げられたボールは必ず落下しながら進み、放物線軌道を描きます。ピッチャーからバッターボックスまでの18.44mという距離を飛翔する野球のボールも、この物理法則からは逃れられません。
しかし野球のストレートは、バックスピンに起因する「マグヌス効果」がボールに揚力を与えることで、通常の放物線よりも浮き上がる=落ちない球となることが知られています。
マグヌス効果については後ほど詳しく解説しますが、こうした回転がボールに力を与え、軌道を曲げるという原理はカーブも同じです。いわばストレートは「上に曲がるカーブ」であるとも言えます。
しかし一方で、「落ちる」変化球として有名なフォークボールも同じくバックスピンで回転しているのです(若干回転数が低いという差はあるものの)。本来ならストレートと同じく落ちない球となるはずが、なぜ逆に落ちるのでしょうか…?
その鍵となるであろう両者の大きな差が、球の握り方(シーム)です。野球のボールは2つの曲面を縫い合わせた形状をしていますが、実はこの縫い目が変化球のキモなのです。
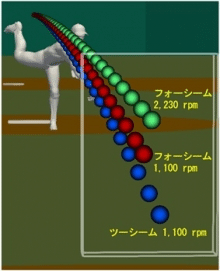
ストレートは4シーム(図左)、フォークは2シーム(図右)で投げます。4シームでは縦回転時に縫い目がほぼ等間隔に、1回転で4回現れます。対して2シームは1回転で縫い目が2回現れますが、これは下記の写真のように片面に集中しており、不等間隔になっているのが大きな違いです。

このシームやボールの回転数、回転方向が、同じボールを自由自在に曲げるのが変化球という技術の面白さでもあります。
さて、こうした諸元によってボールの軌道がなぜ変化するかは経験的に「なんとなく」説明されてきましたが、このメカニズムを流体解析(CFD)によって詳細に解明したのがこの研究です。
◆CFD(数値流体解析)とスパコン
さて、ここでCFDについて少し説明を。
空気のような流体を支配するのはナビエ=ストークス方程式と呼ばれる式なのですが、これは解析解がない(言うなれば「解の公式」が見つかっていいない)式です。
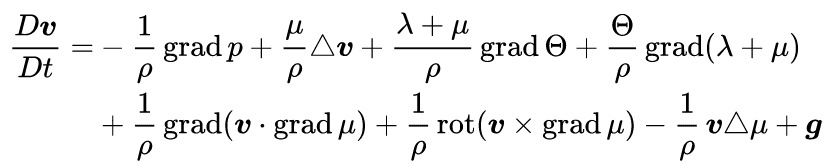
なので空気の流れを計算することはとても難しく、昔は風洞実験などで代用していましたが、コンピュータの計算能力向上により、流体を細かい「格子」に分割して、力任せに繰り返し計算をして解く(数値解を得る)ことが可能になりました。
この手法を数値流体解析:CFDといい、近年は飛行機や自動車の空力設計や、電子機器の冷却設計(熱流体解析)など、空気や水が関係するあらゆるシミュレーションに使われています。


ここで理解すべきポイントは、CFDでは「格子」を細かくすればより詳細な結果が得られますが、一方で計算量が大幅に増加するため、CFDでは精度と計算量(計算時間)は常にトレードオフの関係にあるということです。
そして、今回の研究のようにボールの縫い目の影響まで考慮するには、当然その縫い目よりもさらに小さい「格子」にボールの周囲の空気を分割せねばなりません。これには気の遠くなるような計算量が必要となります。
これを可能としたのが、モデルに施した様々な工夫と、なによりもスパコン(スーパーコンピュータ)の強大な計算力です。

今回計算に使用されたのは、東京工業大学のスパコンであるTSUBAME3.0。東工大所属の全員が使用可能という「みんなのスパコン」ですが、その計算能力は2011年に世界一となったスパコン「京」に匹敵する国内有数のスパコンです。
ちなみに個人レベルのPCと比べた計算力はおよそ数万倍。丸1年かかる計算が5分で終わるほどの差があります。
また2020年に再び世界一位を取った「富岳」の計算能力はさらにこの約50倍なので約6秒で終わります。あるいは50倍に計算量が増えるほど詳細な計算でも可能、ということでもあります。
こうした計算力がもたらす差を見ると、いかにスパコンが私たちの科学技術の進歩に寄与するかということもわかるのではないでしょうか。
さて、少し脇道にそれましたが、こうした強力な計算力によって、ストレートとフォークボールのメカニズムが明らかになります。
◆フォークボールに働く「負のマグヌス力」と流体力学
計算の結果、非常に興味深い結果が得られました。
なんとフォークボールには、通常のバックスピンで生じるボールの上方向へ働くマグヌス力と交互に、ボールの落下方向に働く「負のマグヌス力」が生じていることが明らかになります。

このため、計算によると2シームで投げられたフォークは、たとえ同じ回転数であっても4シームのストレートより打者の手元で19cmも落ちるということです。
(画像:いずれも上記HPより引用)
さて、ここからはこの「負のマグヌス力」の原理を(私見を交えつつ)解説していきます。
この現象を理解するには、流体力学の知識が必要になります。
物体の周囲を流体が流れる時、流体には粘性による抵抗が生じ、これが支配的になる物体近くの領域を「境界層」と呼びます。
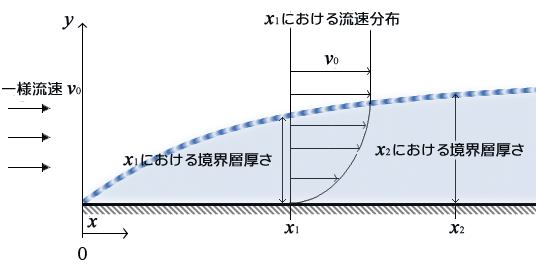
この境界層はいずれ物体後方で表面から剥離し(境界層剥離)、空気の流れを変えていきます。
球を曲げるマグヌス力には、この境界層剥離が関わっています。
ボールがバックスピンで飛翔すると、ボールの下側ではボールと空気の速度差が大きく、上側では小さくなります。
すると、速度差が大きい下側で先にボール表面から境界層が剥離。このため空気が下向きに流れて上下に圧力差が生じ、ボールに揚力が発生する。これがマグヌス効果です。
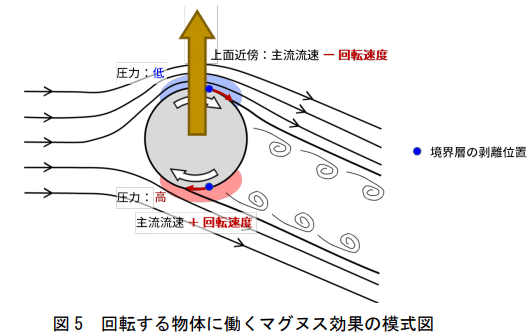
しかし、これは空気流が整って流れる「層流」の場合です。
おそらく2シームの縫い目の不規則性によって、球表面の流れが「乱流」に変化すると、今度は流速の高い下側の方が境界層剥離しにくくなるという逆転現象が起こります。
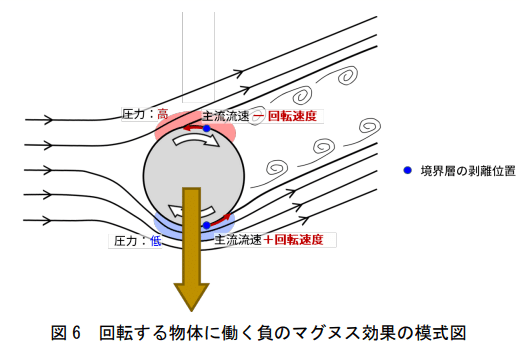
結果、空気は上向きに流れ、球を押し下げる「負のマグヌス力」に転じるわけです。
(図:いずれも慶應大プレスリリース資料より)
つまりストレートとフォークの軌道の違いを生んでいるのは、縫い目が等間隔な4シームでは層流となる境界層が、不等間隔な2シームでは部分的に乱流へ変化するためだと考えられます。
もう少し詳しく言うと、乱流(turbulent flow)とは、流れが整って規則的に(定常的に)流れる層流(laminar flow)に対して、不規則に時を追うごとに変化する流れのことを言います。
層流では粘性抵抗のため、空気は下図のように表面に近い所ほどゆっくり流れます。このため速度差が大きくなると、圧力差により表面付近で空気が逆に流れ始め、境界層剥離を起こします。
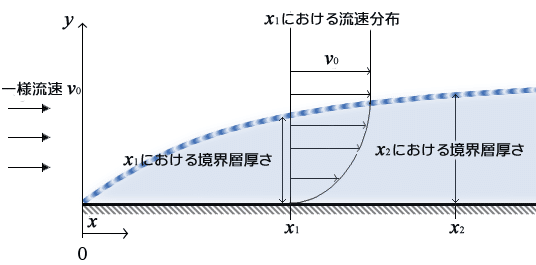
しかし乱流では事情が違い、乱流境界層では表面付近にも速い空気流が入り込みます。すると、層流のように逆流⇒境界層剥離という現象が起きにくくなり、また、むしろより大きく表面の空気の流れが乱れる速度差が大きい場合の方が境界層剥離が起きにくくなるという全く逆の性質に変化するのです。
実は航空機設計にも、境界層をあえて乱流化させることで境界層剥離を遅らせる手法があったりします(境界層剥離は失速の原因となるため)。

目に見えない所で、層流と乱流の間で変化しながら空気が流れ、ボールの軌道が変化していく流体力学的現象が、皆さんの中でイメージできたのなら嬉しいです。
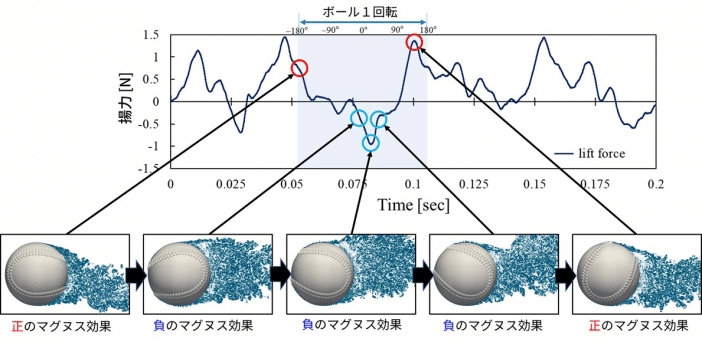
このように、流体の流れというのはかくも不思議で、しかし文字通り私たちの身の回りで様々な現象に影響しているのですね。
◆おわりに
というわけで、フォークボールにまつわる流体力学的現象をCFDにより解明したこちらの研究を解説しました。
スパコンの計算能力が可能にした、ボールの縫い目の影響までもをとらえる高精細な流体解析。それが明らかにしたのは「負のマグヌス力」の存在。その背景には2シームがもたらす層流と乱流の遷移があり、同じバックスピンながら「落ちる」フォークボールを実にうまく説明していえます。
皆さんもキャッチボールでもしながら、流体力学的現象に思いをはせてみてはいかがでしょうか。
というわけで今回の解説はここまで。
お付き合いいただきありがとうございました。
--------------------------------------------------------
注記なき画像は全てWikipediaより引用しています
--------------------------------------------------------
この他にも技術・政治・科学ニュースの解説や、VRやVTuberに関する考察記事を投稿しています。お時間あればぜひごらんください。
また次の記事でお会いしましょう。
--------------------------------------------------------
記事のシェアはこちらから
フォークボールが落ちるワケ:流体解析が説明した「負のマグヌス効果」(思惟かねの科学技術ニュース解説)https://t.co/lFJDmE6R6Z
— 思惟かね(オモイカネ)📕知識系VTuber/Vライター🔔 (@omoi0kane) March 27, 2021
フォークはなぜ落ちるのか?を流体解析で解明した面白い研究を解説しました。
ボールの縫い目が生む流体力学的現象や、研究を支えたスパコンの話にも触れています。
--------------------------------------------------------
今回も長文にお付き合いいただきありがとうございました。
引用RT、リプライ等でのコメントも喜んでお待ちしています。

Twitter: https://twitter.com/omoi0kane
Youtube: https://www.youtube.com/channel/UCpPeO0NenRLndISjkRgRXvA
Medium:https://omoi0kane.medium.com/
Instagram: https://www.instagram.com/omoi0kane/
Facebook: https://www.facebook.com/profile.php?id=100058134300434
マシュマロ: https://marshmallow-qa.com/omoi0kane
○引用RTでのコメント:コメント付のRTとしてご自由にどうぞ(基本的にはお返事しません)
○リプライでのコメント:遅くなるかもしれませんがなるべくお返事します
この記事が気に入ったらサポートをしてみませんか?
