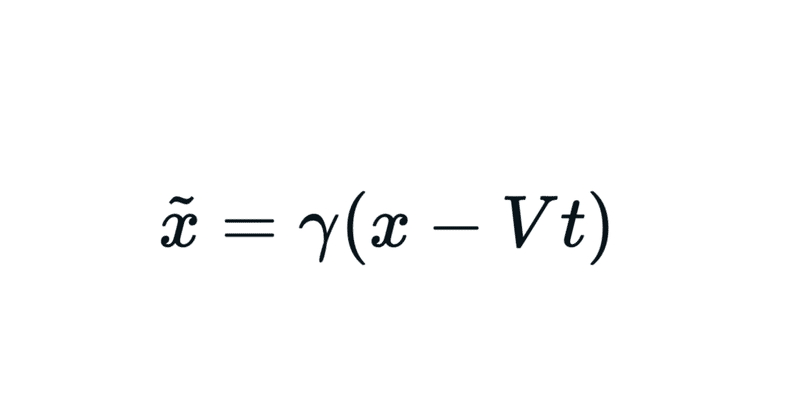
相対性理論の入門、前編
帰ってきた物理学
量子力学は小さな世界で物理量が確率的であることを記述する。一方、相対性理論は大きな世界で時間と空間が歪むことを記述する。
空間を歪ませる正体は速度と重力である。速度を論じるのが特殊相対性理論で、重力を考慮すると一般相対性理論になる。
今日は速度の方を扱う。ちなみに質量とエネルギーもおかしなことになる。
ガリレイと相対性原理
等速直線運動
「位置と時間と速度の関係」
ある物体が時刻$${t}$$に位置$${x}$$にあるとする、このとき速度$${v}$$とは
$$
v = \displaystyle \frac{dx}{dt}
$$
$${x}$$は$${t}$$の関数であることに注意してほしい。$${v}$$も$${t}$$の関数になるが、もし$${v}$$が$${t}$$に依存しないとき
$$
v = V = \displaystyle \frac{\Delta x}{\Delta t} = \displaystyle \frac{x}{t}
$$
これを等速直線運動という。次も成立する。
$$
x = Vt
$$
次も成立する。
$$
t = \displaystyle \frac{x}{V}
$$
単純のため、時刻$${t = 0}$$において位置$${x = 0}$$が成立すると仮定している。
ガリレイ変換
「新幹線に乗った状態で剛速球をなげたらどうなるの?」
2つの物体$${A}$$、$${B}$$を考える。時刻$${t = 0}$$において、$${x_A = 0}$$、$${x_B = 0}$$であるとする。また、$${A}$$と$${B}$$は等速直線運動をしていて、速度がそれぞれ$${V_A}$$と$${V_B}$$であるとする。時刻$${t}$$における$${A}$$と$${B}$$の位置は
$$
x_A = V_A t
$$
$$
x_B = V_B t
$$
このとき、$${A}$$からみた$${B}$$の相対位置は
$$
x_B - x_A = (V_B - V_A) t
$$
つまり、相対速度は
$$
V_B - V_A
$$
当たり前のことをあらためて書いた。これは適当な慣性系から別の慣性系を観測した場合の変換則である。
ある慣性系$${S}$$と別の慣性系$${\tilde S}$$があり、$${S}$$から見て$${\tilde S}$$が速度$${V}$$で等速直線運動しているならば、ある物体の$${S}$$における位置$${x}$$と$${\tilde S}$$における位置$${\tilde x}$$の関係は
$$
\tilde x = x - Vt
$$
また
$$
\tilde v = v - V
$$
当たり前のことをあらためて書いた。これをガリレイ変換という。問題となるのは次の2点
なぜ当たり前だと思うのか
これを否定する実験結果が存在する
1点目は身の回りの現象がそうなっているからである。身の回りの現象はすべてこれで説明できる。異なる慣性系においても物理法則は普遍である(相対性原理)。これは直感的に理解できる。
本稿の趣旨は2点目である。まず、光の歴史を辿っていこう。
光の速度
光に速度は存在するか
あなたが光の速度が有限であることを知ったのはいつだろうか。小学生のときだろうか。それを直接観測したことはあるだろうか。わたしはない。それは人類も同じで、400年前まで光の速度は無限だと思われていた。
ガリレオが活躍したのは1600年代頃になるが、光の速度が有限であるという仮説はこの時代に発想されている。星の軌道の予測と実際の観測時刻が異なるならば、光が「一瞬で届いていない」ことがわかる。
実際にレーマーが観測したのは1670年頃で、この時代の計算結果だと$${2.12 \times 10^8}$$ m/s。ここから進んで、1720年頃のブラッドリーの時代には$${3.01 \times 10^8}$$ m/s と計算される。
光を伝える媒介
天文学に頼らず、光速度を計算できるようになったのはフィゾーの時代である。1849年の回転する歯車を用いた実験で$${3.15 \times 10^8}$$ m/s。
光の波動性を示すヤングの実験が行われたのは1800年頃だが、光は何を媒介にして伝わるのかというのがこの時代の関心事だった。水面波は水を媒介に、音は空気を媒介にして伝わる。光が波であるならその媒介があるはずである。とりあえず、光の媒介をエーテルと呼ぶことにした(エーテル仮説)。
これを検出しようとするのが、1887年のマイケルソン・モーリーの実験である。地球は$${3 \times 10^4}$$ m/s で公転しているから、地球上の物体は「エーテルの風」を受けており、それが光の速度に影響を与えていると考えた(後ろから風を受ければ速くなるし、前から受ければ遅くなる)。この実験は「エーテルの風速」を計算しようとしたが、結果的にはほぼ無風であることが確認された。
この矛盾を説明するためのアイデアがローレンツの収縮仮説である。

速度ではなく距離と時間が変化すると考えた。
アインシュタインと相対性原理
ローレンツ変換
ある慣性系$${S(t, x)}$$と速度$${V}$$で等速直線運動する別の慣性系$${\tilde S(\tilde t, \tilde x)}$$を変換するために
$$
\tilde x = \gamma (x - Vt)
$$
これをローレンツ変換という。「長さが縮む」を数学的に表現する方法として「位置をスカラー倍する」。
$${t}$$と$${\tilde t}$$は一致するとは限らないと注意してほしい。$${\gamma}$$をローレンツ因子と言い、$${V}$$によってのみ決まる。また、慣性系はすべて対等だから$${\tilde S}$$から$${S}$$への変換も同じように行われこれが成立しなければならない。だからその逆変換は
$$
x = \gamma (\tilde x + V \tilde t)
$$
ここで、$${S}$$において速度$${v}$$で等速直線運動していると観測される物体(粒子)が、$${\tilde S}$$において速度$${\tilde v}$$と観測されるとき、これらの関係をローレンツ変換で求めてみよう。
単純のため、$${t = \tilde t = 0}$$のとき、$${x = \tilde x = 0}$$と仮定すると$${x = v t}$$、$${\tilde x = \tilde v \tilde t}$$だから
$$
\tilde x = \gamma (x - Vt) = \gamma (v - V) t
$$
また
$$
x = \gamma (\tilde x - V \tilde t) = \gamma (\tilde v + V) \tilde t
$$
よって
$$
\tilde x x = \tilde v v \tilde t t = \gamma ^ 2 (v - V) (\tilde v + V) t \tilde t
$$
整理すると
$$
\tilde v v = \gamma ^ 2 (v - V) (\tilde v + V)
$$
1次方程式なのでこれを解いて
$$
\tilde v =\displaystyle \frac{v - V}{1 - \left( 1 - \displaystyle \frac{1}{\gamma^2} \right) \displaystyle \frac{v}{V}}
$$
あるいは
$$
v =\displaystyle \frac{\tilde v + V}{1 + \left( 1 - \displaystyle \frac{1}{\gamma^2} \right) \displaystyle \frac{\tilde v}{V}}
$$
$${\gamma = 1}$$ならばガリレイ変換に一致する。$${\gamma \neq 1}$$の場合に$${v}$$を大きくしてみる。
$$
\displaystyle \lim_{v \to \infty} \tilde v =\displaystyle \frac{1 - \displaystyle \frac{V}{v}}{\displaystyle \frac{1}{v} - \left(1 - \displaystyle \frac{1}{\gamma^2} \right) \displaystyle \frac{1}{V}} = \frac{1}{- \left(1 - \displaystyle \frac{1}{\gamma^2} \right) \displaystyle \frac{1}{V}}
$$
$${v}$$を無限にしても$${\tilde v}$$は無限にならない。その値は$${\gamma}$$と$${V}$$で表現できる有限の値に収束する。$${S}$$と$${\tilde S}$$を逆にしても同じである。
これはかなり直感に反するが、この世界がローレンツ変換に従うなら速度は有限であり上限が存在することを示唆する。
歴史の答えとしてはこの上限が光速度であり、これを光速度不変の原理という。光はどの慣性系から見ても同じ速度に見えるが、それはこの世界の速度の限界値である。また、これは物体(粒子)は光の速度を超えられないという意味でもある。
$${v \rightarrow c, \tilde v \rightarrow c}$$とすると
$$
\gamma = \displaystyle \frac{1}{\sqrt{1 - \displaystyle \frac{V^2}{c^2}}}
$$
これを使うと
$$
\tilde t = \gamma \left(t - \displaystyle \frac{V}{c^2} x \right)
$$
また
$$
t = \gamma \left(\tilde t + \displaystyle \frac{V}{c^2} \tilde x \right)
$$
$${c \rightarrow \infty}$$とすると$${\gamma = 1}$$で、$${t = \tilde t}$$となり、ガリレイ変換の世界と一致する。
また、速度にも適用すると速度の変換則が求められる。
$$
\tilde v = \displaystyle \frac{v - V}{1 - \displaystyle \frac{v V}{c^2}}
$$
ただし、これは平行方向のみの計算である(慣性系の速度に対して垂直方向の場合は計算が異なる。本稿では扱わないが簡単なので導出してみてほしい)。
運動量とエネルギー
運動量
$$
p = mv
$$
に対して、ローレンツ変換によって変換した速度を適用すると運動量保存則が成立しない。速度を速くしたり遅くしたりしている成分(速度の変換則より$${\tilde v}$$の分母の第2項)だけずれる。これをずれないようにするには
$$
p = m \gamma v = \displaystyle \frac{mv}{\sqrt{1 - \displaystyle \frac{v^2}{c^2}}}
$$
$${c \rightarrow \infty}$$ならば古典的な運動量と一致する(導出は端折った)。またこれは質量を関数と見れば、速度が大きくなると質量が大きくなるという解釈もできる。
$$
m(v) = \displaystyle \frac{m}{\sqrt{1 - \displaystyle \frac{v^2}{c^2}}}
$$
式を整理すると
$$
\displaystyle \frac{v^2}{c^2} = 1 - \displaystyle \frac{m^2}{m^2(v)}
$$
運動量$${p}$$が有限ならば、「見かけの質量」$${m (v)}$$は有限である。このとき$${c}$$が有限ならば、上式から$${v = c}$$であることと$${m = 0}$$であることは同値である。質量がゼロでないならその粒子は光速度に到達できないし、逆も成り立つ。
運動エネルギーについても修正しよう。結論としては
$$
E = m c^2 \gamma = \displaystyle \frac{m c^2}{\sqrt{1 - \displaystyle \frac{v^2}{c^2}}}
$$
$${\gamma}$$を展開して近似すると
$$
\gamma = 1 + \displaystyle \frac{v^2}{2 c^2} + \cdots
$$
$$
E = m c^2 + \displaystyle \frac{1}{2} m v^2 + \cdots
$$
第1項を静止エネルギーと言う。第2項は古典的な運動エネルギーだ。この式によると、$${v = 0}$$でも運動エネルギーを持つことになる。少しおかしいな?言い換えよう。物体は存在するだけでその質量の分だけエネルギーを持つ。すなわち、質量とエネルギーは等価である。
おわりに
はじめてローレンツ変換をみたとき、なにをどうやったらこんな発想できるのかよくわからなかった。
マイケルソン・モーリーの実験
失敗した実験として世界で最も引用された実験である。ローレンツ変換が信じられるまでにどれだけの実験が繰り返されたか想像もつかない。二重スリットの実験が最も美しい実験であるなら、マイケルソン・モーリーは最も偉大な実験だろう。
歴史の答えとしてはこの上限が光速度であり、
これは少しズルをした。ローレンツ変換は速度の上限があることを説明するがそれが光速度であることを説明しない。どの慣性系から見ても光速度が不変であることはマクスウェル方程式から予言されるが、それが世界の上限と一致するかはこれだけではわからない。光の質量がゼロかどうかもわからない。
物体(粒子)は光の速度を超えられない
これには例外がある。光速度を超える架空の粒子をタキオンと呼ぶが
「はじめから」光速度を超えている粒子があるなら、それがそれよりさらに速くなることを否定しない
そもそも粒子でないなら限界が存在しないことを否定しない
1つ目が観測されたことは今のところない。2つ目について、例えば宇宙(=空間そのもの)の膨張速度は光よりも速い。これは観測事実である。
相対論と量子論はどちらの方が学びやすいか
相対論 → 速度が線形計算でない
量子論 → 確率と虚数が出てくる
観測事実が直感的でないという点は共通している。
おまけ
後編
参考書
この記事が気に入ったらサポートをしてみませんか?
