材料力学第3回　鋼の伸びを求めよう！演習問題2

　前回は材料力学で最も基本的な問題に挑戦しましたね！（前回の記事はコチラ）今回の問題は国家公務員試験などでもよく出題される形式の問題をやっていきます！そういえば、今年の国家公務員は昨今のコロナウイルスの影響で試験が延期になっているだとか...。とても大変な時期ではありますが、就活生の皆さん、めげずに勉強頑張ってください！

　それでは問題です！

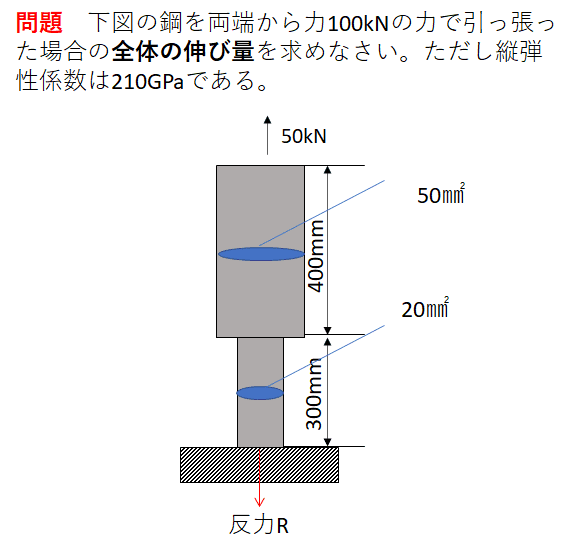
　どうでしょう？いきなり難 しくなったと感じますよね？面積の大きい部分にかかる荷重は50kN？それとも半分の25kN？わかんないですよね！そんな時に有効なのが仮想断面という手法です。今回は仮想断面の解説を中心に問題を解いていきましょう！

今回重要になるのは以下の3stepです。
step1 壁の反力を求める
step2　仮想断面を設定し、各部材の内力、伸びを求める
step3　各部材の伸び量の合計を求める

　step1 壁の反力を求める

　前回までは、あまり意識せずにやってきたと思いますが、壁面に固定されている部材を引っ張った場合、反対方向に引っ張り返す力が働くはずです。これを反力と呼びます。そして、この部材おそらく引っ張った瞬間にどっかへ飛んで行ったり、ひとりでに動き出したりしないですよね（笑）？これは物理用語でいうと力がつり合っている状態にあるといいます。この力のつり合いから、部材に働く力の合計が０になるという等式を立てることができます（0にならなかったらどこかの方向に動いてしまう...→運動方程式を解かなければならない）。具体的には以下の通りです！

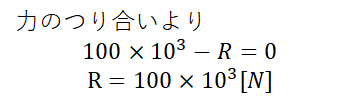
　この力のつり合いは上向きを正、下向きを負にして計算しております。
※ちなみに反力の答えが負になる場合は設定した反力の方向が真逆だったということです！

step2　仮想断面を設定、各部材の内力、伸びを求める

　さて今回の本題です。ここでは、各部材に働く力を求めます！考えてほしいことは、働く力がどこで変化しそうか（実際に変化するかは問題に依ります）というところです。すると、部材Aと部材Bのちょうど間の部分で変化してそうですよね！←断面積が変わってるので！
なので、部材Aの適当な部分（下図の①）と部材Bの適当な部分（下図の②）に分けて考えてあげましょう。

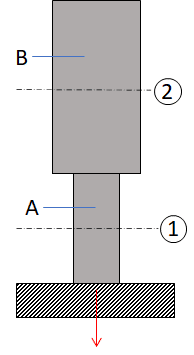
　まず、①に関してです。この部分で区切ったのが以下の図です。部材の各部では内力と呼ばれる力が働いておりこの内力Q1のつり合いにより部材がその形を維持していると考えてください。

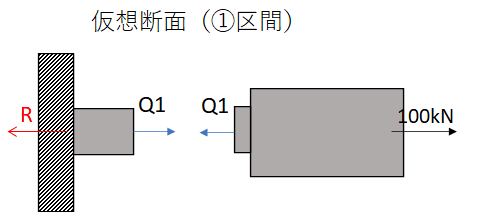
　そして、どちらかの部分における力のつり合いを考えましょう。左でも右でも同じになるのですが今回は左を使いましょうかね！左では反力Rと内力Q1が釣り合っているため、明らかにQ1=R=100×10^3であることがわかります。従ってこの部分の伸びは、公式Δℓ=Pℓ/AE(公式の導出はコチラ)を用いると部材Aの伸びは以下のようになります。

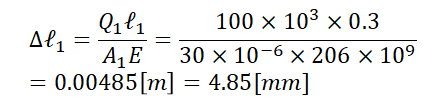
　また、部材Bでの仮想断面は以下のようになり（片方のみ記載）、こちらも力のつり合いからQ2=R=100×10^3となります。

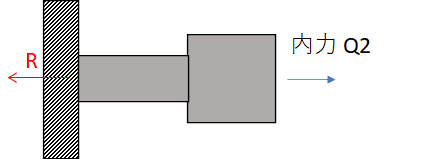
　したがって、この時の伸びは

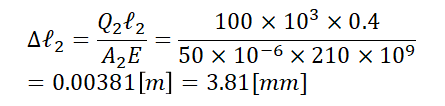
　となります。

step3　各部材の伸び量の合計を求める

問題は、全体の伸びですので各部材の伸びを足し合わせをします。すなわち

が答えになります。

　いかがだったでしょうか？仮想断面という考え方は、初めは慣れないと思います。しかし、これをマスターすると材力の大きなトピックである引張・ねじり・曲げ（梁）のすべてで問題をスムーズに解くことができます。頑張って勉強してください！次回も公務員試験を参考に問題作りをしたいと考えているので、是非とも見ていってください！