
【ZWIFT】身長・体重と空気抵抗の関係~導出編~
前回の記事で身長・体重と空気抵抗の関係について記載しました。
今回は空気抵抗係数をどうやって導き出したかについて書いていきます。
1.空気抵抗と前面投影面積
身長体重が空気抵抗に影響する事は、Zwift Insiderの記事で知っていました。
空気抵抗は以下の式で表されます。
(空気密度×Cd×A×v^3)/2
速度vの3乗に比例
空気抵抗係数Cdと前面投影面積Aに比例
身長・体重の異なる2人のライダーが同じ速度で走っていた場合,空気密度、空気抵抗係数Cd、速度vの3つは同じになります。でも2人のライダーで空気抵抗は違っている。それは前面投影面積Aが違うからです。
zwiftでは、身長・体重が増える→前面投影面積が増える→空気抵抗が増えるとなっていると思われます。
つまり、前面投影面積Aがなんらかの身長・体重の関数として設定されているはずです。
2.仮説・空気抵抗はルート(体重✕身長)に比例する
では、前面投影面積Aを身長・体重の関数として表すことはできないか?
考えてみました。
以下の図のように人間を身長H、幅L、厚みLの直方体とみなします。人間の比重は水とほぼ同じで約1.0のようです。(※プールで空気を吐き出せばちょうど水に沈みます。)このように仮定すれば、人間の前面投影面積A’を身長Hと体重Mの関数で表すことができます。

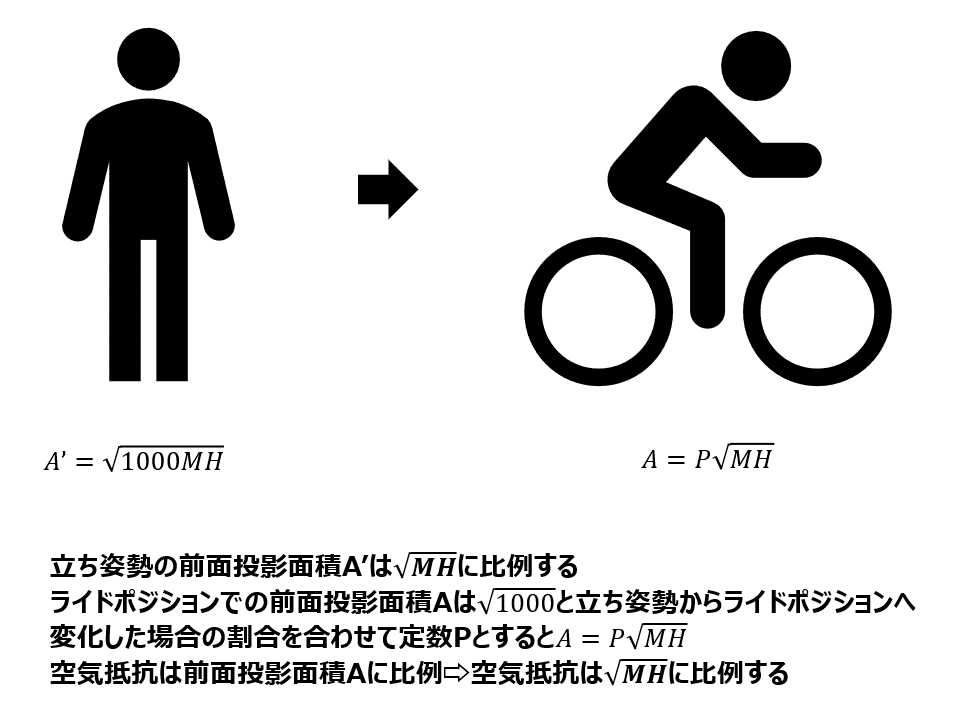
詳細は図を参照いただいて、最終的に言いたいのは、
ライドポジションでの前面投影面積Aはルート(MH)に比例する。
つまり同じ速度で走る時の空気抵抗はルート(体重✕身長)に比例する。
・・・と仮説を立てました。
空気抵抗=(空気密度×Cd✕A×v^3)/2
A=P×ルート(MH)
これに同じ速度・同じ機材という条件を入れて定数をP’としてまとめると
空気抵抗=P’×ルート(MH)
3.検証
Zwift Powerで平坦コース・ドラフティング無効のTTレース結果を見れば、身長・体重・平均出力・タイムを確認することができます。ここから、上記仮説が合っているか検証を試みました。だいたい合ってそうだという感覚は得ましたが、たまに予測から大きく外れるタイムがあります。これは選択した、フレーム・ホイールの差によるものと思われますが、Zwift Powerでは選択した機材まで知ることはできません。
いまいちスッキリしない・・・
仕方ないので実際に走って検証することにしました。
■検証方法
体重70kg身長176cmが3.0W/kgで走った時の速度を基準として、体重・身長が異なる人がこれと同じ速度で走る為の出力を上記計算式から求める。
計算値の出力で走った時に本当に同じ速度になるか確かめる。
※詳しくは結果の表にて
■検証手順
1) コースは Tempus Fugit ※ど平坦なので

2) カスタムワークアウトでFTP100%一定出力のワークアウトを作成→FTPを指定ワットに変えてワークアウトを選択。
ERGモードを選択。これで一定出力で走ることができます。
※スマートトレーナーが必要。
※FTP100%一定のワークアウトを作っておくと、FTPを変えると指定出力を一時的に変えれて便利。

3) 機材はZWIFT TT、ZWIFT 32mm Carbon
※ドラフティング無効にする為TTバイク

4) 身長体重を指定値に変更
5) Tempus Fugitを一周する。計測区間は約2.5km地点のゲートから約20km地点の同じゲートまで。
ゴールのゲートは一回通過して折り返してからゴールなので注意。
6) STRAVAのセグメント"Tempus Fugit(Zwift Insider verified)"のタイムを記録。 ※28:04前後になるはず。

■結果

本編はキリの良さから、体重70kg 身長175cmを基準としましたが、
この時は体重70kg 身長176cm(BMI22.5)を基準として進めました。
基準の⑥体重70kgの3倍、210W一定で走ると、タイムは28:04、平均時速36.96kmでした。他の行を目標値(W)で走った時にこの28:04とほぼ同タイムになれば、今回の仮説が合っていたことになります。
①の体重55kg身長176cmの行を使って説明すると、目標値の列186W(3.38W/kg)が計算で求めた基準と同タイムで走る為の速度です。結果は27:58で6秒早い結果となりました。時速は37.09km/hで基準とはほんの0.13km/h差なので、かなり合っていると言えるでしょう。
補正後の列は、ぴったり28:04で走る為の出力を今回の結果から割出した値です(計算は割愛します)。①の結果は少し早かったので、あと2W少なく184Wならほぼ28:04ぴったりだったはずです。
以上のように検証を進めた結果、最もずれが大きくて④体重55kg身長145cmで22秒、6Wずれでした。
★結論
空気抵抗はルート(体重✕身長)に比例するという仮説はおおよそ合っているけど少しずれる
※ちなみにこの検証は1本走るのに30分かかります。この時腰痛ぎみで30分254Wとか正直厳しい・・・。ということで、同じチームJETTの柴田さんに検証を手伝ってもらいました。柴田さんありがとうございました。
4.補正
検証結果から、より精度の高い関数に補正できないか考えました。

上記は①⑥⑪の身長176cmの結果をプロットしたものです。補正後の出力の点にぴったり合う関数にすれば良いわけですが、ルート(M)の関数ではどうにも合わない。結局単純に体重の1次関数として線形近似した方が良いとの結論に至りました。
■下記表の空気抵抗係数は以下で求まります
(0.5168×体重+0.2601×身長-11.69)/体重
※体重はkg、身長はcm

空気抵抗がルート(ML)に比例するとした場合、体重が増加するに従って傾きが寝てきます(=体重に対する空気抵抗の増加率が鈍化する)。この方が物理的には合っているような気がします。(空気抵抗が体重に比例する根拠があるのだろうか・・・?)
私の仮説通りの設定で走ってみたら
体重が軽い側(55kg)⇨想定より早くなった。
体重が重い側(85kg)⇨想定より遅くなった。
この事からもZwiftでは体重軽い側にやや有利な設定になっている・・・ような気がします。
この記事が参加している募集
いただいたサポートはエクセル365の維持費にしたいと思います。
