折り紙で5次方程式が解けるまでの歩み

「定規とコンパスを使って作図せよ」

みなさん、学校の数学の授業でこのような問題を解いた記憶はあるでしょう。

では、定規とコンパスの代わりに折り紙を使って作図をするとどうなるでしょうか？

折り紙を使って方程式を解くという試みは、これまで多くの数学者を魅了してきました。今日は、その歩みをお伝えできればと思います。

折り紙で方程式を解くとは？

そもそも、折り紙で方程式を解くとはどういうことでしょうか？
順を追って説明していきます。

図1

折り紙で直交座標を引く

作図問題では通常、交わる2直線の交点を求めたり、異なる2点を通る直線を定規で引いたりする操作が認められています。折り紙ではどうでしょうか？

交点を求めるのは良いとして、定規で直線を引くことに相当する操作は、次のように折り目を付けることで代用できます。

(O1) 点$${\textrm{P}_{1}}$$及び点$${\textrm{P}_{2}}$$を通るように折り目$${l_{f}}$$を付ける（図1）

他にも折り紙では次のような折り方が可能なことが分かります。

(O2) 点$${\textrm{P}_{1}}$$を点$${\textrm{P}_{2}}$$に重ねるように折り目$${l_{f}}$$を付ける（図1）

(O2)は、2点を端点とする線分の垂直2等分線を引く操作に相当します。

(O3) 直線$${l_{1}}$$を直線$${l_{2}}$$に重ねるように折り目$${l_{f}}$$を付ける（図1）

(O3)では2直線が交わるとき、折り目が2通り存在します。このように可能な折り目が複数ある時には、それらの中から任意に1つを選んで、実行することとします。

(O4) 点$${\textrm{P}}$$を通り、直線$${l}$$を自分自身に重ねるように折り目$${l_{f}}$$を付ける（図1）

(O4)は点$${\textrm{P}}$$から直線$${l}$$へ垂線を引く操作に相当します（点$${\textrm{P}}$$は直線$${l}$$上にあってもなくても構いません）。

ここで、「直線$${l}$$を自分自身に重ねる」という表現について注意点。この表現には、直線$${l}$$に沿って折り目$${l_{f}}$$を付ける操作も含まれるように感じるかもしれません（$${l = l_{f}}$$）。しかし、そのような折り方は本質的に何もしない操作と変わりないので考えないことにします。

さて、これらの操作を認めると紙の上の任意の場所に直交座標を引くことが可能になります。

直交座標の引き方（図1）

まず、任意の場所に$${x}$$軸に相当する直線を折ります。$${x}$$軸上に任意に原点$${0}$$と単位点$${1}$$を取ります。

次に、(O4)の折り方で原点$${0}$$を通り$${x}$$軸に垂直な直線を折り、これを$${y}$$軸とします。

(O3)で、$${x}$$軸を$${y}$$軸に重ねるように折り目を付けます。折り目は2通り存在しますがどちらを選んでも構いません。この折り目に対して(O4)を行うことで$${x}$$軸上の点と$${y}$$軸上の点とが互いに移りあうことを確認しましょう。

最後に、$${x}$$軸上の単位点$${1}$$に対応する$${y}$$軸上の点を、$${y}$$軸における単位点$${1}$$とします。

紙の上の任意の点に対して、$${x}$$軸及び$${y}$$軸への垂線を引くことによって$${x}$$座標と$${y}$$座標を取得できます。任意の点の座標がこれで表現できるようになります。

折り紙で四則演算を行う

直交座標ができたので、$${x}$$軸や$${y}$$軸上の点に実数を対応させることを考えます。そのためにはそれらの点に対して四則演算（加減乗除）に対応する操作を折り紙で行う必要がありますが、これについても可能です。

加減を行う方法（図1）

$${x}$$軸上に2点$${a}$$及び$${b}$$が与えられたとき、$${a+b}$$及び$${a-b}$$に対応する点を$${x}$$軸上に取ることを考えます。

まず、点$${b}$$を$${y}$$軸に移し、垂線を引くことで$${x}$$軸に平行な直線$${y=b}$$を作ります。

点$${(0,1)}$$及び点$${(1,0)}$$に対して(O2)を使って、原点を通る傾き$${1}$$の直線$${y=x}$$を作ります。

点$${a}$$を通り直線$${y=x}$$に垂直な直線を引き、さらにそれに垂直な直線を引くことで、直線$${y=a\mp x}$$を作ります。

それぞれの直線と直線$${y=b}$$との交点の$${x}$$座標が$${a-b}$$及び$${a+b}$$になります。

乗除を行う方法（図1）

$${x}$$軸上に2点$${a}$$及び$${b}$$が与えられたとき、$${a\times b}$$及び$${a\div b}$$に対応する点を作ることを考えます。

まず、点$${b}$$を$${y}$$軸に移し、垂線を引くことで$${x}$$軸に平行な直線$${y=b}$$を作ります。

直線$${x=1}$$と直線$${y=b}$$との交点と原点を通る直線$${y=bx}$$を作ります。
直線$${y=bx}$$と直線$${x=a}$$との交点の$${y}$$座標が$${a\times b}$$になります。

同様に、直線$${x=a}$$と直線$${y=b}$$との交点と原点を通る直線$${y=\frac{b}{a}x}$$と直線$${x=1}$$との交点の$${y}$$座標が$${a\div b}$$になります。

これでようやく折り紙で方程式を解くとはどういうことか説明できます。

折り紙で方程式を解くとは、求めるべき方程式の各係数の値が$${x}$$軸や$${y}$$軸上の点として与えられた状態から始めて、折り紙を折る操作を繰り返すことで新たに点や直線を作っていき、最終的に方程式の解となる値を$${x}$$軸や$${y}$$軸上の点として求めるための具体的な手続きを示すことである

折り紙で3次方程式が解けるまで

これで原理が説明できたので、実際に方程式を解いていきましょう。

図2

折り紙で2次方程式を解く

四則演算ができるので1次方程式が解けるのは良いでしょう。では、2次方程式はどうでしょうか？

作図問題では、コンパスで円を描いて直線との交点を求めたりしますが、折り紙において次の折り方がコンパスの代用になっています。

(O5) 点$${\textrm{P}_{2}}$$を通り、点$${\textrm{P}_{1}}$$を直線$${l}$$上に重ねるように折り目$${l_{f}}$$を付ける（図2）

(O5)では、点や直線の配置によって折り目の付け方が0,1,2通りと変わるのでご注意を。

(O5)を認めると、任意の正実数に対して平方根を求めることが可能になります。

平方根$${\sqrt{a}}$$の求め方（図2）

点$${\textrm{P}}$$:$${(0,1)}$$、点$${\textrm{Q}}$$:$${(0,-a)}$$及び直線$${l}$$:$${y=-1}$$を描きます。

(O5)を使って、点$${\textrm{Q}}$$を通り点$${\textrm{P}}$$を直線$${l}$$上に重ねるように折り目を付けます。

この折り目と$${x}$$軸との交点が求める平方根$${\sqrt{a}}$$になります。

※補足
折り目と$${x}$$軸との交点を$${\textrm{X}}$$とおくと、$${\textrm{OP}:\textrm{OX} = \textrm{OX}:\textrm{OQ}}$$が成り立ちます。

2次方程式の解の公式から、四則演算と平方根の組み合わせで解が求まるので、折り紙で2次方程式が解けることが分かります。

折り紙で角の3等分ができた！

定規とコンパスを使った作図では、角の3等分や任意の数の立方根を求めることは不可能であることが知られていますが、折り紙ではどうでしょうか？

1980年、日本の学会誌『数学セミナー』に折り紙による角の3等分の方法が掲載され話題を呼びました。

阿部 恒; 『数学セミナー』1980年7月号 日本評論社

角$${\theta}$$の3等分の方法（図2）

長方形$${\textrm{ABCD}}$$において、$${\angle\textrm{BAE} = \theta}$$となるように辺$${\textrm{DC}}$$上に点$${\textrm{E}}$$を取ります。

辺$${\textrm{AD}}$$上に任意に点$${\textrm{F}}$$を取ります。さらに、点$${\textrm{A}}$$と点$${\textrm{F}}$$に対して(O2)を使って垂直2等分線を引き、辺$${\textrm{AD}}$$及び辺$${\textrm{BC}}$$との交点をそれぞれ$${\textrm{G}}$$、$${\textrm{H}}$$とします。

点$${\textrm{F}}$$を直線$${\textrm{AE}}$$上に重ね、かつ点$${\textrm{A}}$$を直線$${\textrm{GH}}$$上に重ねるように折り目を付けます。

この折り方によって点$${\textrm{A}}$$の移る先の点を$${\textrm{A}'}$$とするとき、$${\angle\textrm{BAA}'=\theta /3}$$となります。

※補足
点$${\textrm{F}}$$の移る先の点を$${\textrm{F}'}$$とするとき、$${\angle\textrm{A}'\textrm{AF}=\angle\textrm{FA}'\textrm{A}=\angle\textrm{FA}'\textrm{G}+\angle\textrm{GA}'\textrm{A}=2\angle\textrm{BAA}'}$$が成り立ちます。

阿部氏によるこの方法をよく見てみると、今までにない折り方が使われていることに気付きます。

(O6) 点$${\textrm{P}_{1}}$$を直線$${l_{1}}$$上に重ね、かつ点$${\textrm{P}_{2}}$$を直線$${l_{2}}$$上に重ねるように折り目$${l_{f}}$$を付ける（図2）

(O6)では、点や直線の配置によって0,1,2,3通りの折り目の付け方が存在します。

実は、この折り方が折り紙に3次方程式を解く能力を与えているのです。例えば、任意の立方根を求めることも可能です。

立方根$${\sqrt[3]{a}}$$の求め方（図2）
点$${\textrm{P}}$$:$${(0,1)}$$、点$${\textrm{Q}}$$:$${(-a,0)}$$及び直線$${l}$$:$${y=-1}$$、直線$${m}$$:$${x=a}$$を描きます。

(O6)を使って、点$${\textrm{P}}$$を直線$${l}$$上に重ね、かつ点$${\textrm{Q}}$$を直線$${m}$$上に重ねるように折り目を付けます。

この折り目と$${x}$$軸との交点が求める立方根$${\sqrt[3]{a}}$$になります。

※補足
折り目と$${x}$$軸との交点を$${\textrm{X}}$$、$${y}$$軸との交点を$${\textrm{Y}}$$とおくと、$${\textrm{OP}:\textrm{OX} = \textrm{OX}:\textrm{OY} =\textrm{OY}:\textrm{OQ}}$$が成り立ちます。

角の3等分と立方根が求まると、カルダノの公式により任意の3次方程式を解くことが可能になります。さらにフェラーリの公式により、3次方程式が解ければ4次方程式も解けるので、折り紙によって任意の4次方程式まで解けることがこれで分かりました。

これらの事実は1980年代から90年代にかけて複数の研究者によって相次いで発表されますが、実は50年以上昔の1936年にベロッホによって既に証明されていたことが判明しています。

M. P. Beloch; Sulla risoluzione dei problemi di terzo e quarto grado col metodo del ripiegamento della carta, Scritti Matematici Offerti a Luigi Berzolari, 1936.

折り紙の公理ができ上がるまで

折り紙作図の可能性が広がってくると、折り紙でどこまでのことができるのか疑問が湧いてきます。

そんな中で、折り紙の折り方を公理化しようという動きが生まれます。

第7の折り方が存在する！

図3-1

1989年、藤田氏はこれまで登場した6つの折り方を公理として規定しました（図3-1上）。

藤田 文章; Axiomatic Development of Origami Geometry, Proceedings of the First International Meeting of Origami Science and Technology, Humiaki Huzita, ed., 1989, pp143-158.

2001年、羽鳥氏がこれまでの折り方では規定できない第7の折り方を発見します（図3-1上）。

羽鳥 公士郎; 折り紙による作図

(O7) 点$${\textrm{P}_{1}}$$を直線$${l_{1}}$$上に重ね、かつ直線$${l_{2}}$$を自分自身に重ねるように折り目$${l_{f}}$$を付ける

(O7)では、直線$${l_{1}}$$と直線$${l_{2}}$$が平行でないときに限り、折り方が1通りに定まります。

ただ、これら7つの折り方はジュスタン氏によって1986年に既に発見されていたことが判明しています。

Jacques Justin; Résolution par le pliage de l'équation du troisième degré et applications géométriques (1986)

2004年、ラング氏は1回で1つだけ折り目を付ける折り方（以後、単純折りと呼ぶ）は(O1)から(O7)までの7種類ですべてであることを証明しました。

R. J. Lang; Origami Approximate Geometric Constructions, in Tribute to a Mathemagician, Barry Cipra, Erik D. Demaine, Martin L. Demaine, and Tom Rodgers, eds., A K Peters, 2004.

ラング氏の着眼点は以下の通りです。

例えば、(O7)の折り方を見てみると「点$${\textrm{P}_{1}}$$を直線$${l_{1}}$$上に重ねる」と「直線$${l_{2}}$$を自分自身に重ねる」の2つの操作に分解できることが分かります。

このように、これ以上分解できない基本操作（これをラング氏に倣いアライメントと呼ぶことにします）の組み合わせですべての折り方が定義されるわけです。

ラング氏は、単純折りのアライメントが5種類しかなく、これらの組み合わせで表現される折り方は7種類しかありえないことを突き止めたのでした（図3-1下）。

これによって単純折りで方程式を解く能力の限界も明らかになったのです。

---

定理1
単純折りによって一般の3次方程式を（したがって4次方程式も）解くことはできるが、一般の5次方程式を解くことはできない

---

多重折りの定式化へ

図3-2

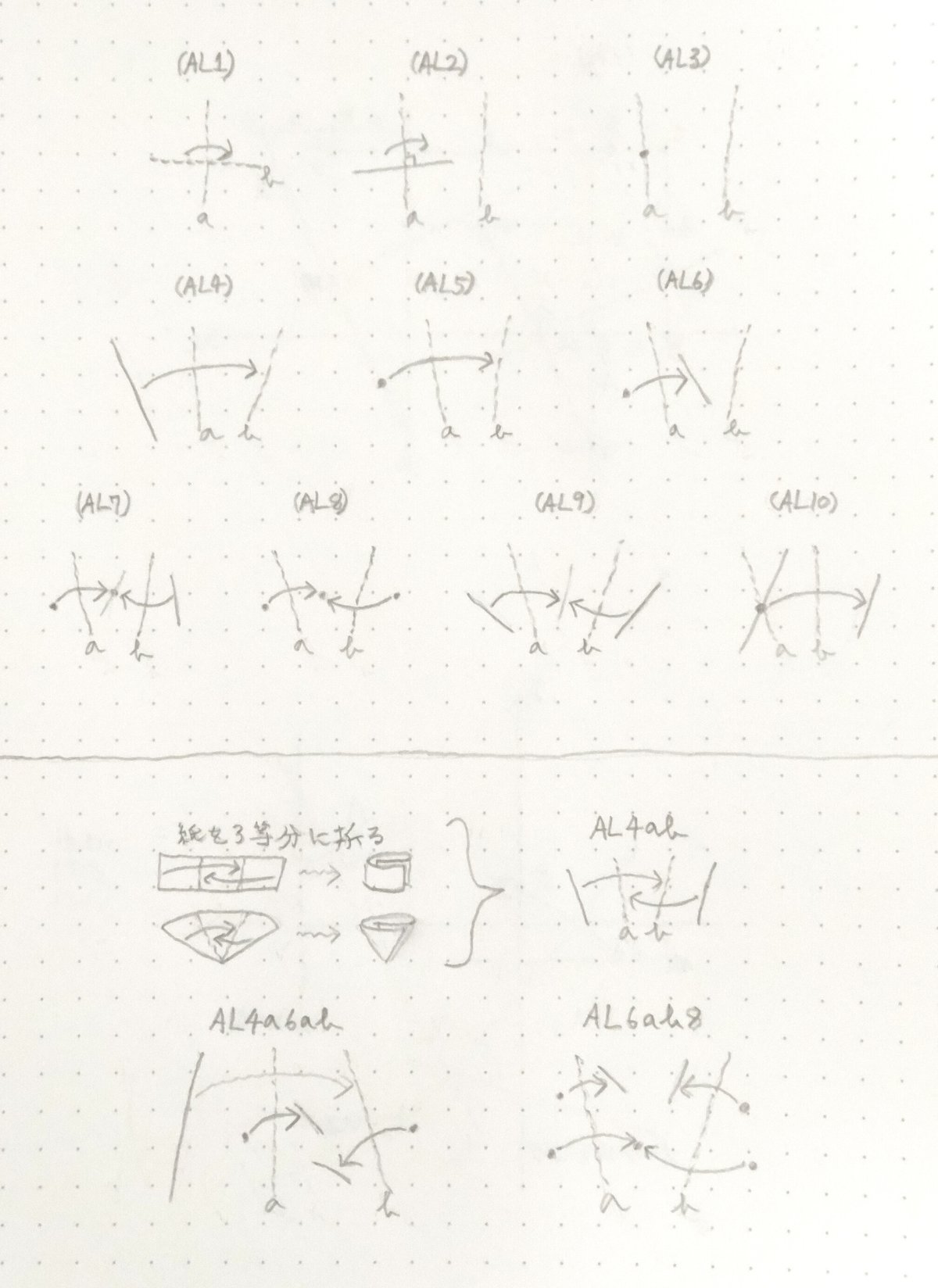
単純折りについては以上で決着がついたわけですが、これより他に折り方は存在しないのでしょうか？

例えば、紙を3つに折るときを考えてみましょう（図3-2下）。

普段、我々が何気なくやっている折り方をよく見てみると、1回の操作で同時に2つの折り目を付ける折り方になっていることが分かります。このように同時に複数の折り目を付ける折り方を多重折りと呼ぶことにします。

ラング氏は同時に2つの折り目を付ける2重折りで角の5等分を実現しました。多重折りでこれまで解けなかった方程式が解けることが示されたのです。

Robert J. Lang; Angle Quintisection (2004)

さらにラング氏の研究は続きます。

アルペリン氏とともに、2重折りに対するアライメントが10種類であることを突き止め（図3-2上）、すべての2重折りがこれらの組み合わせで表現されることが分かったのです（図3-2下）。3重折り以降も同じようにして考えることができます。

多重折りの定式化がこうして示されたのでした。

Roger C. Alperin and Robert J. Lang; One-, Two-, and Multi-Fold Origami Axioms (2006)

2重折りで5次方程式が解けた！

ガロア理論によって、一般の5次方程式の解の公式が存在しないこと、より正確には四則演算とべき根をとるという操作の組み合わせで解を求めることは不可能であることが知られています。

では、折り紙ではどうでしょうか？

図4

3重折りによる5次方程式の解法

実は、多重折りを認めると、リルの方法による方程式の解法を応用して任意の代数方程式を折り紙で解くことができるようになるのです。

---

定理2
高々$${(n-2)}$$重折りによって一般の$${n}$$次方程式を解くことができる（$${n\ge 3}$$）

---

ここでは、$${n=5}$$の場合について手順を示します。

3重折りによる5次方程式の解法（図4上）

5次方程式$${x^5+ax^4-bx^3+cx^2+dx-e=0}$$が与えられているとします（図の都合上、係数の正負の符号を恣意的に変えています）。

まず、点$${\textrm{P}}$$:$${(0,-1)}$$及び直線$${l_{1}}$$:$${y=1}$$を描きます。

次に、原点に点$${\textrm{A}}$$を取り、線分の長さが各係数の値になるように折れ線$${\textrm{ABCDET}}$$を描きます（$${\textrm{AB}=a}$$、$${\textrm{BC}=b}$$、$${\textrm{CD}=c}$$、$${\textrm{DE}=d}$$、$${\textrm{ET}=e}$$）。

点$${\textrm{E}}$$から線分$${\textrm{ET}}$$とは逆の方向に$${e}$$だけ進んだ位置に、直線$${l_{2}}$$を線分$${\textrm{ET}}$$に垂直となるように引きます。

次の条件をすべて満たすように3つの折り目$${f_{a}}$$、$${f_{b}}$$、$${f_{c}}$$を付けます。

(1) 折り目$${f_{a}}$$によって、点$${\textrm{P}}$$が直線$${l_{1}}$$上に重なる
(2) 折り目$${f_{b}}$$によって、点$${\textrm{T}}$$が直線$${l_{2}}$$上に重なる
(3) 折り目$${f_{a}}$$と線分$${\textrm{BC}}$$との交点$${\textrm{Y}}$$、及び折り目$${f_{b}}$$と線分$${\textrm{CD}}$$との交点$${\textrm{Z}}$$の両方を折り目$${f_{c}}$$が通る
(4) 折り目$${f_{c}}$$によって、折り目$${f_{a}}$$及び折り目$${f_{b}}$$がそれぞれ自分自身に重なる

このとき、折り目$${f_{a}}$$と$${x}$$軸との交点$${\textrm{X}}$$が、与えられた方程式の解となります。

※補足
点$${\textrm{E}}$$から$${x}$$軸への垂線と折り目$${f_{b}}$$との交点を$${\textrm{W}}$$とおくと、$${\textrm{OP}:\textrm{OX}=\textrm{XB}:\textrm{BY}=\textrm{YC}:\textrm{CZ}=\textrm{ZD}:\textrm{DW}=\textrm{WE}:\textrm{ET}}$$が成り立ちます。

2重折りによる5次方程式の解法

上の通り、高々3重折りによって5次方程式が解けることが分かったわけですが、角の5等分に関してはラング氏の方法による2重折りの作図が存在します。

2013年、西村氏は任意の5次方程式を解くのに3重折りは必要ないことを証明しました（単純折りでは解けないわけですから、これが5次方程式に関するかぎり最良の結果となります）。

西村 保三; Solving quintic equations by two-fold origami (2013)

---

定理3
2重折りによって一般の5次方程式を解くことができる

---

ここでは、『数学セミナー』に掲載された手順を紹介します。

西村 保三; 「折り紙で5次方程式を解く」『数学セミナー』2014年4月号 日本評論社

2重折りによる5次方程式の解法（図4下）

5次方程式$${x^5+ax^3+bx^2+cx+d=0}$$が与えられているとします（カルダノ変換によって4次の項を消去しています）。

ここで、幾多ある2重折りの中で以下の折り方に着目します。

点$${\textrm{P}}$$:$${(0,1)}$$、点$${\textrm{A}}$$:$${(p,q)}$$、直線$${m}$$:$${y=-1}$$、直線$${n}$$:$${x=k}$$及び直線$${l}$$:$${\alpha x+\beta y+1=0}$$に対して、次の条件をすべて満たすように2つの折り目$${f_{1}}$$、$${f_{2}}$$を付ける
(1) 折り目$${f_{1}}$$によって、点$${\textrm{P}}$$が直線$${m}$$上に重なる
(2) 折り目$${f_{2}}$$によって、点$${\textrm{A}}$$が直線$${n}$$上に重なる
(3) 折り目$${f_{1}}$$によって、直線$${l}$$が折り目$${f_{2}}$$に重なる

5つの変数$${\alpha}$$、$${\beta}$$、$${k}$$、$${p}$$、$${q}$$を上手く選ぶことによって、折り目$${f_{1}}$$と$${x}$$軸との交点が、与えられた方程式の解となるようにするのが目的です。

満たすべき条件は以下の5つの式に帰着されます。
$${(\alpha^2+\beta^2)k=(\beta^2-\alpha^2)p+2\alpha\beta q+2\alpha(1-6\beta)}$$
$${0=8\alpha\beta p+4(\beta^2-\alpha^2)q-4(\alpha^2-2\beta^2+\beta+\alpha^2 a)}$$
$${2(\alpha^2+\beta^2)k=-6(\beta^2-\alpha^2)p-12\alpha\beta q+4\alpha(\beta-\alpha b)}$$
$${0=-8\alpha\beta p+4(\beta^2-\alpha^2)q-4(\beta+\alpha^2 c)}$$
$${(\alpha^2+\beta^2)k=(\beta^2-\alpha^2)p+2\alpha\beta q-2\alpha(1+2\alpha d)}$$

最初と最後の式、及び2番目と4番目の式から
$${\{9(a+c+1)-2d^2\}\alpha^2+2d\alpha+4=0}$$
$${3\beta=d\alpha+1}$$
となります。

ここで、判別式$${D=d^2-4(a+c+1)\ge 0}$$のときは$${\alpha}$$の実数解が求まるので、残りの式から$${\beta}$$、$${k}$$、$${p}$$、$${q}$$も求まります。

判別式$${D=d^2-4(a+c+1)<0}$$のとき、$${d=0}$$なら自明な解$${x=0}$$がありますので、$${d\neq 0}$$とします。このときは$${x=\varepsilon x'}$$と変数変換して$${\varepsilon}$$を十分小さく選べば、$${D\geq 0}$$にできます。

※補足
一般に、点$${(p,q)}$$及び直線$${\alpha x+\beta y+\gamma =0}$$（ただし、$${(\alpha,\beta)\neq(0,0)}$$）は折り目$${\varphi x+\psi y+\omega =0}$$（ただし、$${(\varphi,\psi)\neq(0,0)}$$）によって、
それぞれ点$${(\frac{p(\psi^2-\varphi^2)-2\varphi(q\psi+\omega)}{\varphi^2+\psi^2},\frac{q(\varphi^2-\psi^2)-2\psi(p\varphi+\omega)}{\varphi^2+\psi^2})}$$及び直線$${\{(\psi^2-\varphi^2)\alpha-2\varphi\psi\beta\}x+\{(\varphi^2-\psi^2)\beta-2\varphi\psi\alpha\}y+\{\varphi^2\gamma-2\varphi\omega\alpha-2\psi\omega\beta+\psi^2\gamma\}=0}$$に移ります。

まとめ

今日は、折り紙による方程式の解法について、調べられる範囲でお伝えしました。

折り紙を使った作図には数々の意外な発見があり、それがこれまで多くの数学者を魅了してきた理由だと思います。

みなさんも、折り紙作図に挑戦してみてはいかがでしょうか？

#夏の自由研究