
灘中学2024(2日目)終了!
かなり批判的なことを書いてきましたが、最後の大問はよくできていると思いました。お見せします。

紙の上に書かないで数え上げました(それはそれで私の場合危なっかしいのですが…)。
この問題は面白かったですね。というのもヤミクモに数え上げるのではなく、重複や漏れがないように注意しながら予め自分で適切な制約をかけて、いかに調べる手間を省くかというところで勝負ができるからです。探索アルゴリズムといいましょうか、アルゴリズムを考えるという発想の端緒になる問題です。素数や三平方の定理知りませ~ん!という受験生もこの問題では何の問題もありません。自分でアルゴリズムを考え、より良いものはないかという探究心というか向上心をもって問題に取り組むという姿勢はコンピュータサイエンスの基本中の基本だと思います。自分で自分をSTEM教育しているような小学生はサクサク解決したことだろうと思います。
極端ではありますが、コンピュータにこの問題を解かせるときに、A~Iの数列を生成して調べるというアルゴリズムでは、9!=362880通りの数列を作成して、条件分岐でチェックしていくというものが考えられますが、これは正しい(しコードを書きやすい)けれども効率が悪いでしょう。
人間にはとても無理な話です。
しかも、(ア)で学んだことを(イ)で活かせるというのもいいですね。その場で学んでそれを活かすというアタマの使い方は非常に重要なのではないかと考えます。事前準備も必要なし、場合の数をネチネチやる問題でもありません。すでに学んだ知識を再利用する。これはイイ!
圧巻は最後の問題です。思考過程を書くと下のようになりますが、私ごときでも1分で解けます(賢い子なら秒殺!?)。
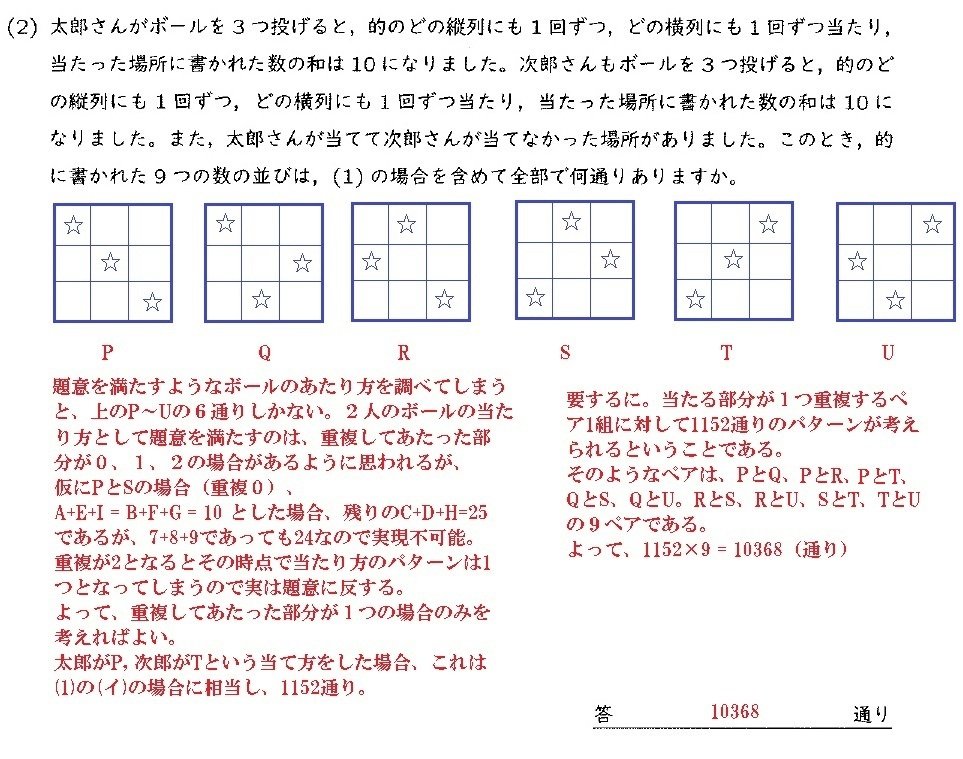
実質的な計算は掛け算1回で終了するというワケです。
素数やら何やらを執拗に責めてくると思いきやラスボス(?)は非常に良問ではないですか!
私が今まで出会ってきた、「数学の嗜みがある方々」は概ね、「メンドクサイことは嫌い!」という志向性を持っていました。メンドクサイことは嫌いだからより優れた解法を志向する。コードを書くにしても、なるべく再利用できるようにという志向性で書く。この問題でいえば、1152を求めるプロセスは同じなのでそれを再利用するということですね。
サヨナラ逆転ホームラン!!!
思うに灘中学の試験問題作成チームの中にある種の確執があるのではないでしょうか?一応(ここは「一応」では済まないでしょうが)名の通った学校の試験問題であれば、チームを組んで検討しながら作成していくことでしょう。このチームの中には執念深いウエットなタイプのメンバーと思考経済的志向性をもつドライなメンバーがいて、学力観に相違があるけれども表向きは大人同士のお付き合いをしている結果が問題に垣間見えるような気がします。
あるいは、メンバー全員が総体として敢えて二重人格的なアウトプットをしているのかどちらかだと思います。
しかし、執念深いタイプの出題であれば、逆に対策は立てやすいですね。手口としては素数を使うというとかですよ。そんなに論点は多くはならないです。
2025年度について考えると、パッと思いつくのは 2+ 0 + 2 + 5 = 9なので9の倍数というのがありますが、これは簡単すぎますね(笑)。素因数分解すると3^4×5^2なので、約数の個数は、(4+1)×(2+1)=15個であり、それらの約数の総和は、(3^0 + 3^1 + 3^2 + 3^3 + 3^4)×(5^0 + 5^1 + 5^2)なので、121×31= 3751となりますが、121=11^2ですし31は素数です。3751は当然素数ではありませんが、11と31がフォーカスされたりするかも。
ちなみに11の倍数であるかどうかのチェックについては私が前にここに書いています。
それと、立体角(立体図形の頂点に集まる各面がつくる角)が直方体の立体角と同じ(90°が3つ集まっている)場合にそれを使えば求積に使えるという話や切断についての議論は1日目に続いて出ており、1日目の問題の見直しをした受験生の方が取り組みやすいのではないかと思えることもありましたね。
もちろん専門家ではないので、そういう方々から見れば素人考えと一笑にふされてしまうかもしれませんが、素人だからこそ見えることもあるのではないかと思います。
まあ、色々書いてきましたが、何度もいいます。
終わり良ければ総て良し!だねっ、灘中学さん!!!
