見出し画像

医療とテクノロジーの交差点にて【第10話】プログラミングすれば頭脳王・河野玄斗に対抗できる説

医者ハッカー けいみー

皆様ごぶさたしてます、トア・ルドクターです。
仕事やプライベートが忙しく更新が滞っていましたが、2020年に入り比較的時間ができまして、youtube鑑賞に明け暮れる今日この頃です。普段は「ゆゆうた（ピアニスト）」「朝倉未来（格闘家）」「ぬりぼう&さわきん（ナンパ師）」などガイジ系を中心に鑑賞させて頂いているのですが、一方で「ヨビノリたくみ」「クイズノック」など教育系youtuberのチャンネルを利用して勉強に励んでいます。最近だと、河野玄斗さん（理III / 司法試験合格 / 頭脳王優勝）が教育系チャンネルを始めていまして、そのチャンネルで興味深い問題があったので今回扱おうと思います。

元ネタの動画（twitter）

問題

【Snow Plow Problem（海外で有名な数学の難問）】
It starts snowing in the morning and continues steadily throughout the day.
A snowplow that removes snow at a constant rate starts plowing at noon.
It plows 2 miles in the first hour, and 1 mile in the second. What time did it start snowing?
ある日、午前中に雪が降り始めた。雪はつねに一定のペースで降る。
除雪車が正午ぴったりに動き出し、1時間で2マイルの除雪を完了し、さらに1時間で1マイルの除雪を完了した。雪はいつ降り始めた？
（単位時間の除雪量は一定 = 除雪車の移動速度は絶えず変化）

前回【第９話】の記事同様、こういう難問でもプログラミングを用いれば簡単に解決できるよ！というのが本記事の趣旨になります。今回は正解コードを先に提示して、小分けして解説していきます。最後に数学的な正攻法の解答もお示しします。

解答コード

# 積雪速度を1とする（楽なので）
# 積雪開始をt=0とすれば、除雪車が動き始めたt=Tで積雪量T
# 除雪車の速度は、その瞬間の積雪量h(t)に反比例する
# 従って　V = k/h(t) だがk=1とする（楽なので）
# Vは連続変化するので本来は微分方程式を解くしかないが
# 1秒ごとに区切って、Vが離散的に変化すると近似する

# t=Tからt=T+3600[s]までの移動距離X1の近似
def x1(T):
   res = 0
   for i in range(3600):
       v = 1 / (T + i)
       res += v
   return res

# t=Tからt=T+7200[s]までの移動距離X2の近似
def x2(T):
   res = 0
   for i in range(3600, 7200):
       v = 1 / (T + i)
       res += v
   return res

# 求めたいのはTの値。Tを1から大きくしていき条件を検討
# 最初はX1のが圧倒的に大きいので、X1/X2 < 2となれば終了
T = 0
ratio = 2
while ratio >= 2:
   ratio = x1(T) / x2(T)
   T += 1
ans = T//60
print(ans)

コードを読むだけでも分かる人には分かるかもしれませんが、１つ１つ順を追って解説していきましょう。​

雪が降り始めた時刻をt = 0とし、積雪車が動き始めた時刻（正午）をt = T[秒]とします。この定数Tを求めるのがゴールであり、求めた答えが T = 3600[秒]だったとすればAM 11:00に雪が降り始めたと分かります。数学でもプログラミングでもゴールを明確に意識する「目的意識」が至極大切なので「Tを求める」ことを念頭に解き進めていきましょう。

ひとまず単位に拘泥せず、簡便化のため積雪速度を1[mm/秒]とすれば、時間 t[秒] の時点では t[mm] の雪が積もっていることになります（このmmとかの単位もぶっちゃけどうでもいい）。除雪車は除雪量が一定になるように動くので、除雪車の速さは積雪量に反比例するというのがこの問題のキモです。これを踏まえると、時間tにおける積雪車の速度V(t)は積雪量t[mm]に反比例するので、比例定数kを用いて V(t) = k / t と表せますが、簡便化のため k = 1とし、V(t) = 1 / t ということにします。このような強引な設定が許されるのは、１マイルとか２マイルといった距離の単位はどうでもよく「最初の１時間で進んだ距離と次の１時間で進んだ距離の比が１：２である」ことが本質だからです。比を扱う上で最終的に比例定数kは消えるので、はなからk = 1としたり積雪速度1としたりして全く問題ないのです。

【ここまでのまとめ】
雪が降り始めた時刻　t = 0
積雪車が動き始めた時刻　t = T [秒]
積雪速度　1 [mm/秒]
時間tでの積雪量　t [mm]
ゴールは、Tを求めること！
--------------------------------------
時間tでの速度V(t) = 1 / t　と設定したので、
t = T[秒]のとき、V(T) = 1 / T（動き始めの速度）であり、
t = T+1[秒]のとき、V(T+1) = 1 / (T+1)
t = T+2[秒]のとき、V(T+2) = 1 / (T+2)
t = T+●[秒]のとき、V(T+●) = 1 / (T+●)
・・・以降、同様に考えることができます。

さて、違和感なく読み進めている人もいると思いますが、これだと１秒ずつ飛び飛びの時点での速度（離散的な値）しか考えていないというピットフォールがあります。実際には、除雪車の速度は絶えず連続変化しており、たとえば V(T+0.001) =  1 / (T+0.001)といった速度も考慮しないといけないため、正確な移動距離を求めるには速度を時間積分する必要があります（数学的には微分方程式を解くのが正攻法）。

とは言っても、上述のように１秒ずつの速度変化を追うだけでも大凡の答え（近似値）は求まります。もちろん、0.1秒ずつ追えばより正確だし、0.01秒ずつ追えばかなり正確な答えが得られますが、どこまでいってもコンピューターが扱うことができるのは離散的な値に過ぎないのです。以上を踏まえて、ここでは１秒ずつの速度変化を追う形で妥協しておきましょう。

先ほどの解説を踏まえると、最初の１時間での移動距離X1は、
X1 = V(T)*1[秒] + V(T+1)*1[秒] + V(T+2)*1[秒] + ... + V(T+3599)*1[秒]
　　= V(T) + V(T+1) + V(T+2) + ... + V(T+3599)
と近似されます。実装はpythonの基本書レベル。

# t=Tからt=T+3600[s]までの移動距離X1の近似
def x1(T):
   res = 0
   for i in range(3600):
       v = 1 / (T + i)
       res += v
   return res

同様に、次の１時間での移動距離X2は、
X2 = V(T+3600) + V(T+3601) + V(T+3602) + ... + V(T+7199)
と近似されます。

# t=Tからt=T+7200[s]までの移動距離X2の近似
def x2(T):
   res = 0
   for i in range(3600, 7200):
       v = 1 / (T + i)
       res += v
   return res

これで漸く準備が整ったので、距離の条件を処理してTを求めます。
「X1が２マイル相当、X2が１マイル相当」という条件から「X1 / X2 = 2という比率になるTを求めればいい」とわかります。プログラミング的にアプローチするには、T = 0,1,2...と片っ端から当てはめていき上記条件を満たすTを探すことになります。T = 0のときはX1がかなり大きく、Tを十分でかくするとほぼX1 / X2 = 1になることをイメージすれば、T = 0,1,2... と大きくする中で、X1 / X2 が2を下回るタイミングを捕まえればいいわけです。以上をwhile-文で実装したのが次のコードです。

# 求めたいのはTの値。Tを1から大きくしていき条件を検討
# 最初はX1のが圧倒的に大きいので、X1/X2 < 2となれば終了
T = 0
ratio = 2
while ratio >= 2:
   ratio = x1(T) / x2(T)
   T += 1
ans = T//60
print(ans)

出力は T = 2226[秒] → ans = 37[分] となり、答えは AM 11:23 だと分かります。最後に数学的な解法を示しておきます。

数学的解法（おまけ）

【問題設定の確認】
雪が降り始めた時刻　t = 0
積雪車が動き始めた時刻　t = T [時]　・・・今回は時間単位！
時間tでの速度V(t) = k / t　（敢えてkは残す）
これらの条件下でTを求めていく。

画像1

画像2

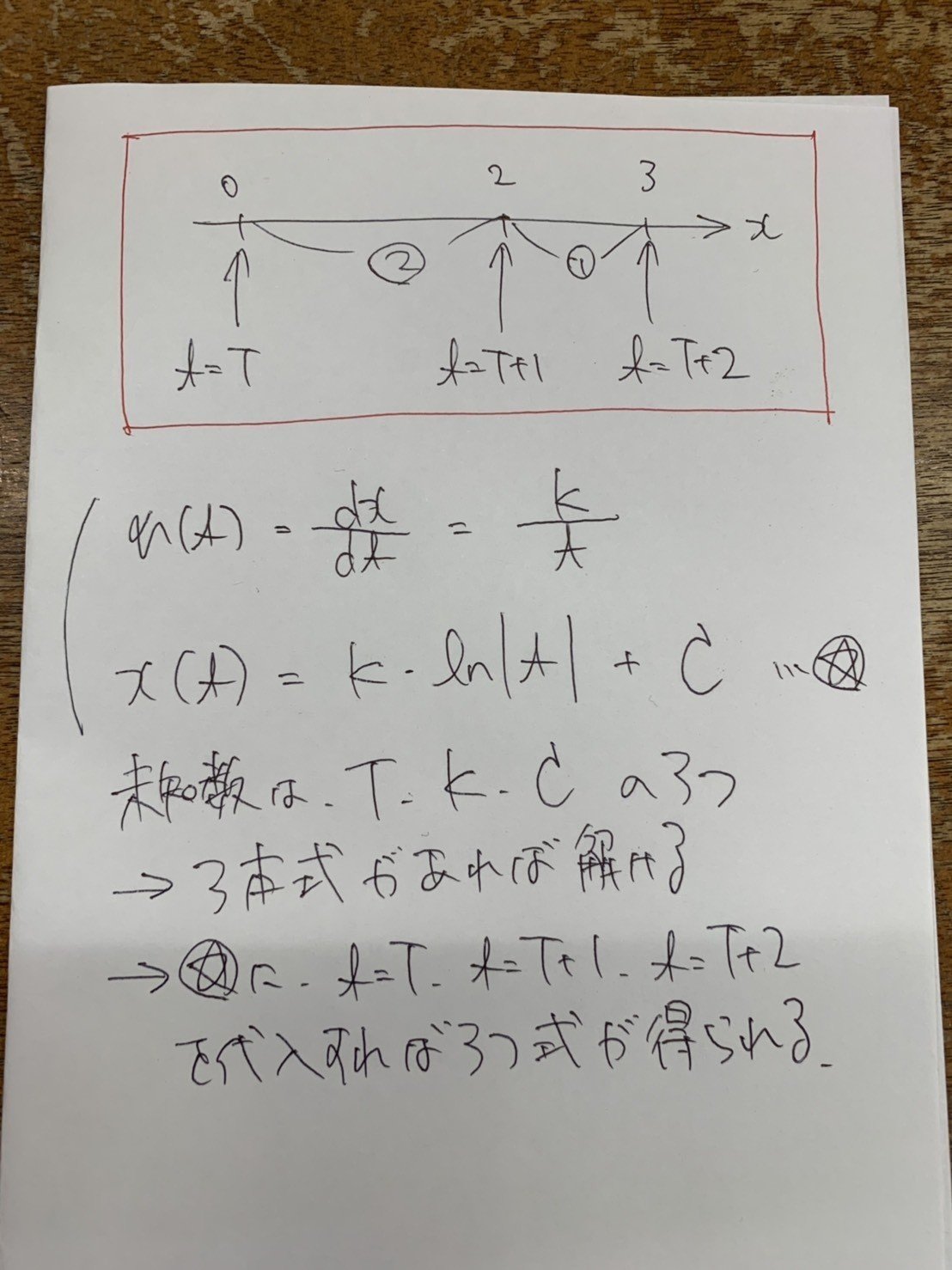
なぜ比例定数kを敢えて残したかですが、②'のところでkの存在を忘れて ln(T+1 / T) = 2 を解こうとしてしまうリスクがあるからです。プログラミングの解法で触れた通り、大切なのは比率なので「②'の３倍と③'の２倍が等しい」という解き方をすれば全く問題ないのですが、ln(T+1 / T) = 2 を単体で解けると誤解してしまうと泥沼にはまります。

では、また！

【著者プロフィール】
都内で医師として研鑽する傍ら、独学でプログラミングを学ぶ26歳。趣味は『ギター / バイオリン / 美術鑑賞 / youtube鑑賞 / 創作料理 / 囲碁 / チェス / 折り紙 / スノボ / サーフィン / ドライブ』など枚挙にいとまがない。CIAの格闘武術クラブマガを始める。得意料理はバナナシチュー。略歴としては高２で数学全国１位（駿台）、文系で官僚をめざすも、ドラマ『コードブルー』の影響から気づいたら医師に。ディープラーニングG検定、統計検定２級、知的財産検定３級など取得。TOEIC 730（泣）。
【記事アーカイブ】
【第１話】医者なのにプログラミングを勉強してみた話
【第２話】pythonプログラミングの小技（１）ラムダ
【第３話】プログラミング初心者が学ぶべき３つのポイント
【第４話】競技プログラミングのススメ
【第５話】競技プログラミング物語（１）バイトリーダーの苦悩
【第６話】プログラミングで自作する実用アプリ（１）NEVER-NOTE
【第７話】プログラミングで解析したDNA鑑定の精度
【第８話】統計学は最強の学問であるのか？
【第９話】プログラミングすれば人類最高IQに対抗できる説
【第10話】プログラミングすれば頭脳王に対抗できる説


この記事が気に入ったらサポートをしてみませんか？