
線形代数学で4行4列つまり4次正方行列の行列式を余因子展開で求める方法 【実用数学】
この記事では、行列の行列式の求め方を説明しています。線形写像は、行列で表すことができるのですが、この行列式の値が0でなければ、その行列の逆行列が存在するということになります。
そのため、行列式を具体的に計算することができると、逆行列が存在するかどうかを確かめることができます。
また、逆行列が存在するとき、その線形写像は、線形同型写像(全単射である線形写像)であり、その逆写像を表すのが逆行列ということになります。ちなみに、線形同型写像の逆写像も線形写像になっています。
この記事では、行列式の計算に絞って、解説をしていきます。行列式は、行数と列数が同じになっている正方行列について考えます。
まず、2次正方行列についての行列式を解説し、その後で、3次正方行列について説明します。
3次正方行列の行列式については、ファンデルモンドの求め方があるのですが、3次限定の求め方なので、4次以上の正方行列でも使える余因子展開を用いた行列式の求め方を解説します。
2次正方行列の行列式

行列Aに対して、その行列式のことを|A|と表します。
※ detA と表すこともあります。
いずれにせよ、2次正方行列についての行列式の求め方はシンプルで、「(1, 1)成分×(1, 4)成分-(1, 2)成分×(2, 1)成分」を計算した値が、行列式の値となります。具体的な行列で、この通り求めてみます。
2次正方行列の場合の具体例

「(1, 1)成分×(1, 4)成分-(1, 2)成分×(2, 1)成分」は、ちょうどクロスに成分を掛け合わせた後に、引けばよいので、覚えやすいかと思います。
1 × 4 - 2 × 3 = -2 となり、|A| = -2 です。
行列式の値が0でないので、この行列は逆行列をもつということになります。
3次正方行列の行列式
3次以上の行列について、行列式を求めるには、余因子展開がやりやすいです。この方法については、次の図をご覧ください。

符号の(-1)については、順番に1ずつ大きくすることで、交互に符号が入れ替わります。厳密には、この図は1列目についての余因子展開といいます。1列目の成分が上から順に掛けられています。図では、目立つように、白色でそれぞれの1列目の成分の値を表しています。
<1列目についての余因子展開>
それぞれの白色の成分と掛け合わせている2次正方行列の行列式は、(1, 1)成分と掛け合わせるのが、はじめの3次正方行列から1列目と1行目を除いた残りの成分でできている行列の行列式となります。
(2, 1)成分と掛け合わせるのは、1列目と2行目を除いてできる行列の行列式です。
(3, 1)成分と掛け合わせるのは、1列目と3行目を除いてできる行列の行列式です。
このように、2次の行列式と掛け合わせるのが、どれも1列目の成分となっているのが、1列についての余因子展開です。
3次正方行列の場合の具体例

実際に手を動かして計算すると、習得しやすいです。
この具体例の3次正方行列の行列式の値は0となりました。行列式の値が0となると、逆行列をもたないということになります。このときは、線形同型写像ではありません。
ここまで、1列目についての余因子展開で行列式を計算しました。1行目についての余因子展開も計算でき、1列目についての余因子展開をしたときと同じ値になることが、すでに証明されています。
<1行目についての余因子展開>
(1, 1)成分と掛けるのは、1行目と1列目を除いた残りの行列の行列式。
(1, 2)成分と掛けるのは、1行目と2列目を除いた残りの行列の行列式。
(1, 3)成分と掛けるのは、1行目と3列目を除いた残りの行列の行列式。
必ず1行目の成分を掛けているので、1行目についての余因子展開といいます。
以上で、行列式の余因子展開の方法の説明を終了します。さらに、行列式の基本変形と合わせることで、効率よく行列式を計算できます。
行列式と基本変形
2次や3次の正方行列ですと、余因子展開だけで計算ができるかと思いますが、4次や5次の正方行列でも行列式を計算しようとしたときに、できるだけ楽に行列式を計算したくなります。そこで役に立つのが、行列の基本変形です。この変形を行うことで、行列式を計算しやすい形に変形して計算できます。
【行列式の性質】
ある行のc倍を別の行に加えても行列式の値は変わらない。
ある列のc倍を別の列に加えても行列式の値は変わらない。
※ここで、cは定数です。実数成分の行列のときは実数、複素数成分の行列のときは複素数です。
この行列式の性質を、数学科の線形代数学の講義では、厳密に証明されるのですが、厳密証明を飛ばして、やり方だけをシンプルな例を使ってお伝えします。
具体例

上の行列式を計算で求めたいときに、行列の基本変形を使って、「1行目の-4倍を3行目に加えた」下の行列式を使って行列式を計算します。下の行列式の方が、余因子展開をしたときに0が出てきて消えるところが出るので、計算しやすいです。
先ほどの行列式の性質から、行列式の値は変わらないということが、数学的に証明されているので、同じ値になるのなら、計算しやすい方で行列式の値を求めるというわけです。
1列目で余因子展開

基本変形をしたので、余因子展開をしたときに、0が出てきました。そのおかげで、0を掛けると値は0になるので、第(3, 1)余因子を計算しなくても良いということになります。結局、第(1, 1)余因子だけを計算すれば良いということになりました。これは2行2列の行列式なので、すぐに計算で値が求められます。
第(1, 1)余因子を計算

今まで、すべて等式でつながった式変形なので、この-42が、求めたかった一番はじめに書いていた3行3列の行列式の値です。
ここからは、4行4列(4×4)の行列、つまり4次正方行列の行列式(determinant)を、シンプルな例を使って、余因子展開と行列の基本変形を使って求めることを説明します。
やり方としては、まず行列の基本変形をして、4行4列の行列式を簡単な形に変形します。それから、それぞれの余因子を求めるということになります。ただ、4次正方行列についてのそれぞれの余因子は3行3列の行列式の計算をしなければなりません。余因子の値を求めるときに、繰り返し行列の基本変形を行い、計算を効率良く求めることがオススメです。
はじめに行列の基本変形
「ある行のc倍を他の行に加えても、行列式の値は同じ」という行列式の性質があります。この性質を利用して、行列式を求めるときに、より計算しやすい形に変えてから、行列式を計算します。では、具体的な4次正方行列について、行列式を計算します。次の図をご覧ください。まず、行の基本変形から実行します。

上に書いている|A|が求めたい行列式です。行列Aの1行目を1倍したものを2行目に加えます。さらに、1行目を-2倍したものを4行目に加えます。そうすると、下に書いている行列式に変形できます。
行列式を計算するときに、どちらも同じ値になることが、数学的に証明されていますので、計算しやすい方で計算して良いことになります。下の方の行列式の方が、1列目で余因子展開をしたときに、0倍が多く出てきて、ほとんどの余因子が消えます。そのため、下の行列式の方が、ずっと計算がしやすいです。では、1列目で余因子展開をします。
1列目で余因子展開

先ほど言った通り、第(2, 1)余因子、第(3, 1)余因子、第(4, 1)余因子には0が掛けられるので、0に消えてしまいます。このため、これら3つの余因子の値を計算しなくても、どうせ0になってしまうので良いということになります。
行列の基本変形を行うことで、行列式の計算を効率良くできるようになります。では、残った第(1, 1)成分の余因子を計算するということになります。①より、第(1, 1)成分の余因子の値を計算して、-1を掛けると、求めたい|A|の値となります。
第(1, 1)成分の余因子の値
残った第(1, 1)成分の余因子は次の図のようになります。

この余因子の値を計算するときに、3行3列の行列の行列式を計算するということになります。
ここで、繰り返し処理の発想で、行列の基本変形をして、計算しやすくします。「3行目の1倍を1行目に加える」ということと、「3行目の1倍を2行目に加える」という基本変形をすると、下の行列式になります。
これで、また、0が多く出てくる形にしたので、2列目で余因子展開をすると、スムーズに行列式の値が計算できます。

2行2列の行列式を計算
0を掛けると値が0になるということから、計算する箇所は最後の項の1つだけになります。後は2行2列の行列式さえ計算すれば、第(1, 1)成分の余因子の値が求まります。
|A|の値を求める

第(1, 1)成分の余因子の値は66です。一番はじめの図の①に、この66を代入すると、|A| = -66 となります。これで、求めたかった4行4列の行列式の値が求められました。
このように、数学では、プログラミングでもよく使われる繰り返し処理の発想が大切になります。
この行列式の計算は、余因子展開によって、よりサイズの小さい正方行列の行列式を求めるということの繰り返しになります。
4次正方行列の行列式を求めるときには、余因子の値を計算するときに3次の正方行列の行列式を求めることになり、3次の正方行列の行列式を求めるときには、その余因子を求めるときに2次の正方行列の行列式を求めることになります。
行列の余因子
n次正方行列Aについて、この行列Aからi行とj列を取り除いてできる(n-1)次の小行列の行列式に、「-1の(i + j)乗」を掛けた値を行列Aにおける第(i, j)余因子といいます。
このように、数学の用語がや文字が並ぶと、はじめて学習するときに苦しくなります。こういうときは、シンプルな具体例で様子を見ると内容が分かってきます。n=3のときの3次正方行列を使って、余因子とは何かということを説明していきます。次の図をご覧ください。

3次の正方行列から、i=2, j=3 のとき、 つまり、2行と3列を取り除いたときを例に、第(2, 3)余因子を求めます。
この図では、まず2行目と3列目を取り除いた小行列を作り、その行列式の前に「-1の(2 + 3)乗」を掛けています。
値を計算すると、第(2, 3)成分の余因子は6と分かります。
※小行列は2次正方行列なので、その行列式はクロスに成分を掛けてから引くと値が求まります。2次正方行列の行列式の求め方はこちらの記事で説明しています。
行列式を余因子展開で計算できるようになると、逆行列を計算することもできます。
逆行列を求める公式
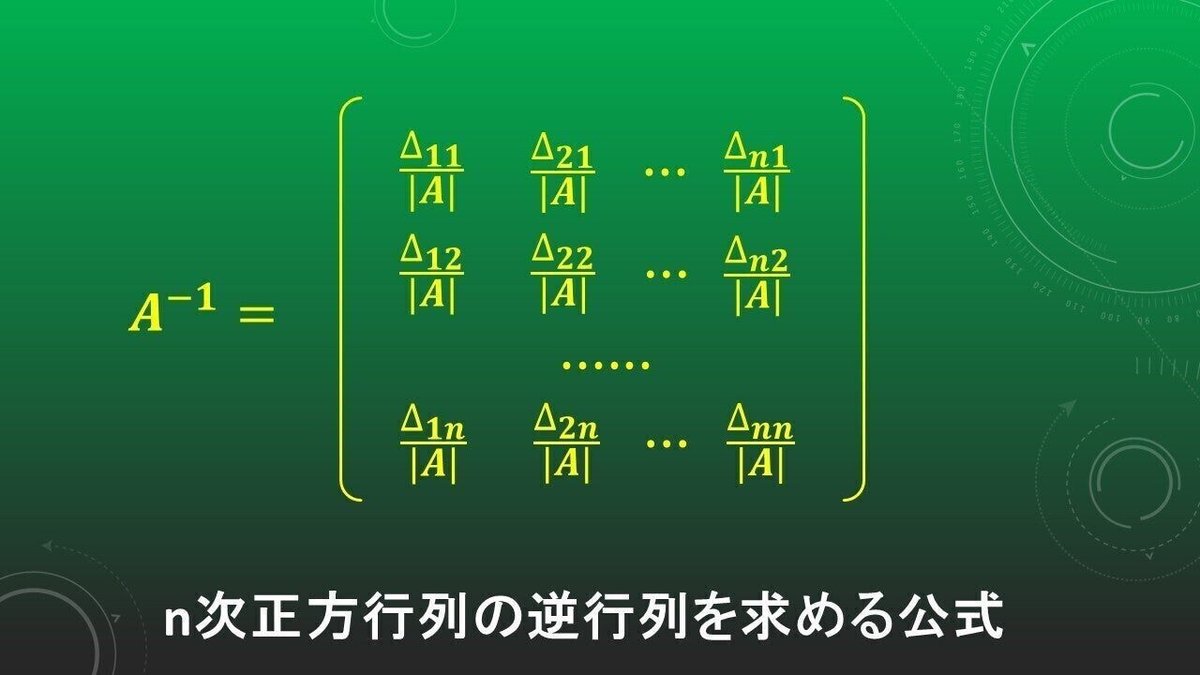
この図に書いているのは、n次正方行列Aの逆行列を求める公式です。見た目が複雑そうなので、注意点を書いておきます。行列Aの逆行列を計算できるのは、行列式|A|の値が0でないときになります。もし|A| = 0 となっているときに、逆行列のどの成分も分母に0がきてしまうので求められないと記憶しておくと覚えやすいです。
大学の線形代数学の講義だと、「n次正方行列Aが逆行列をもつことの必要十分条件が、|A|の値が0でない」ということを厳密に証明するかと思いますが、これを証明するのには結構な記述量が必要になります。
厳密な証明を理解しなくても、ただ単に逆行列を求めたいという場合のやり方だけなら、上で書いている公式に当てはめれば完了なので、手っ取り早く逆行列を求めたい方向けにやり方だけを書いています。
逆行列を求める手順
まず、n次正方行列の行列式が0でないとき、第(1, 1)成分から第(n, n)成分までの余因子を求め、行列式|A|を計算します。
そして、上の図の公式に当てはめれば逆行列が得られます。
このときに、逆行列の(i, j)成分の余因子の添え字が(j, i)と逆になるので注意です。例えば、逆行列の(1, 2)成分に使われる余因子は、添え字が(2, 1)成分となります。
この公式に当てはめるためには、それぞれの余因子を計算して求める方法と、もとの行列の行列式を求める方法を押さえておく必要があります。
具体例で逆行列を求める
では、具体的な3行3列の行列Aについて、逆行列を求めます。行列Aは次の図に書いている行列です。

この図に書いている逆行列を求める公式を使うためには、行列Aの行列式|A|を求める必要があります。ちなみに、線形代数学の一般論で、行列式が0である行列には、逆行列が存在しないので、まず行列式を計算して、値が0になっていないことを確かめます。
行列式を計算するときには、余因子展開を使います。1行目について余因子展開をします。この段階で、第(1, 1)成分、第(1, 2)成分、第(1, 3)成分の余因子の値も求まります。

第(1, 1)成分の余因子の値が1、第(1, 2)成分の余因子の値が0、第(1, 3)成分の余因子の値が1なので、余因子展開の公式から行列式|A|は次のように計算できます。
|A| = 0 × 1 + (-1) × 0 + 1 × 1 = 1
これで、行列式|A|の値が1と求まりましたので、逆行列を求める公式で、それぞれの成分の分母にくる値は1ということになります。逆行列の公式を使うためには、あと一息、残りの余因子たちの値を求めます。

この図をいきなり見ると複雑そうですが、今までのnote記事で余因子展開を具体的に計算してきた余因子の求め方と同じ求め方をしています。
第(2, 1)成分の余因子の値が3、第(2, 2)成分の余因子の値が2、第(2, 3)成分の余因子の値が2、第(3, 1)成分の余因子の値が1、第(3, 2)成分の余因子の値が1、第(3, 3)成分の余因子の値が1となっています。
先ほどの |A| = 1 と、第(1, 1)成分の余因子の値が1、第(1, 2)成分の余因子の値が0、第(1, 3)成分の余因子の値が1であることと合わせて、逆行列を求める公式に代入すると、行列Aの逆行列が求められます。

これで行列Aの逆行列が求められました。この逆行列を求める公式のおかげで、余因子展開(それぞれの余因子を求めること)を計算することができれば、逆行列を求めることができます。ですので、余因子展開をしっかり計算できるようになることが大切になります。
関連するブログ記事
ベクトル空間についての抽象論の出発点については、こちらの岩井の数学ブログの記事で説明をしています。
岩井の数学ブログ(iwai-math-blog)のサイトマップはこちらになります。
では、記事を終了します。
