
解析的ストックフロー一貫成長モデル:富、生産、分配、成長への統合的なアプローチ
日本におけるストックフロー一貫アプローチ(SFCA)の注目度は依然高くない状態が続いており、SFCAに触れている本においても、多くは非常に抽象的な紹介にとどまっており、日本語でSFCAの中身に触れている論文は非常に僅かです。(大野隆&西洋, 2011. etc…)
またSFCAを紹介している日本語論文でも、そのすべては数値解析的な手法で行われており、解析的に解けるアプローチで書かれた日本語文献は、ほぼ存在していません。ですので解析的に解ける政府部門込みのSFCモデルを紹介します。
(数学は好きですが得意ではありません。ですのできっと間違えてるはずなので、見つけたらTwitterに連絡いただければ幸いです)
これは一般的にシミュレーションで行われるSFCモデルを解析的に求めるアプローチで、私にとって元となったアイディアはEckhard Heinの2008年の本「The macroeconomics of finance- dominated capitalism – and its crisis」の第五章と、Marc Lavoieの2014年に出版された「Post-Keynesian Economics New Foundations」の第六章に記載されていたカレツキアンモデル達です。
このアプローチを取るうえで、ポストカレツキアンモデルのアプローチを多く使用しています。したがって、前提知識として初歩的なポストケインジアンの枠組みを知っている必要があります。もしご存じでなければ、僭越ながら私が過去に書いた記事等をご覧になっていただければ、イメージが多少はつかめると思います。
前提、仮定、世界観とか…
負債の発行はオーバードラフトで、負債を主に発行するのは政府と企業になります。家計の負債は現時点では考慮しません。(この時点で構造としては古い経済体制になってしまします。家計負債を考慮すれば、より現代に近い形にできるでしょう)
すべてのトランザクションは銀行口座上の取引で行われ、主体は現金の保持を一切行いません。つまりPure Credit economyが仮定されており、この特性上、準備預金不足による銀行危機は排除されます。
政府部門は中央銀行と政府を統合した概念で、生産手段を持たない存在と仮定して、民間の生産能力を間借りします。
企業は代表的・集計的企業を表し、一財のみを作るとします(レオンチェフ型生産関数を採用)価格の決定はターゲットリターン式を採用し、価格水準は短期と中期は所与、長期では可変とします。
家計は労働者階級と資本家階級を統合した概念で、利潤として配当と利息を受け取り、所得として賃金を受け取ります。銀行は民間銀行の集合を表し、利潤を稼がず、自己資本を持たないと仮定します。
政府支出は、常に最大生産可能量の一定の割合になると仮定し、税収は総所得の関数とし、常に総所得から一定の割合を徴収します。
企業は成長最大化行動と費用最小化行動をとり、生産のための労働供給は無限とし、稼働率に合わせて非常に柔軟に雇用が変動すると仮定し、在庫投資の蓄積は無く、技術革新も考慮しない事とします。
投資は純利益と借入で行い、新規株式発行による資金調達を明示的には考慮せず、株式時価の変動と、それに伴う配当の変化のみを扱います。
インフレーションについては本格的には考慮せず、分配調整・実物制約の際のみに出現するモノとし、産業予備軍効果やフィリップスカーブは省きます。(一応言及はします)
また分析は短期と中期と長期に分けます、これらの違いは以下の通りです。
短期:ストックは固定、期待&予測が完成されるまでを分析
中期:期待&予測は完成済み、ストックの定常状態を分析
長期:期待&予測とストックは完成済み、通常稼働率と長期均衡稼働率が同値になるまでの調整過程を分析
行為主体の行動
家計に関しては現状の収入と持てる預金より支出し、消費性向・貯蓄性向は所与とします。消費行動が終了した後に租税が請求・徴収されます。
企業は稼働率の予測値を中心に投資量を決定し、その投資は借り入れと純利益より行われます。純利益で賄えない場合は当座借り越しを積み上げることになり、それは非常に柔軟に行われます。
先ほど書いた通り、銀行は矮小化させています。しかしその本質的役割は非常に重要で、今回政府部門が加わったことにより、かなり複雑なオペレーションをしています。利潤・自己資本を持たないと書きましたが、これは稼げたはずの利益をすべて分配してしまうからです。HPMがあるため、企業の当座借り越しは預金量より少なくなり、預金金利は当座借越金利よりも小さくなければいけません。政府支出・新たな当座借越しによって起こる口座内金額の変化に伴うこれら金利の調整は素早く行われるとします。
また最後に政府ですが、政府は常に最大生産量の一定割合になるように支出すると仮定しました、これはより分かりやすく言うと「稼働率100%時のGDPの○○%になるよう支出している」という事です。
今回はレオンチェフ型生産関数を使用している+労働供給が無限と仮定しているため、資本係数が定数となり、資本蓄積率はそのまま最大生産量の成長率となります。つまり政府は民間の生産能力成長率に合わせて政府支出を増大させているという事です。
バランスシートマトリクス&ストランザクョンマトリクス
今回使用するバランスシートマトリクスとトランザクションマトリクスは、政府部門を含めたモノとなっています。これまで使用してきたバランスシート&トランザクション・マトリクスは、政府を含まない形の”民間のみ閉鎖体系”でした。またマトリクス自体もGodley&Lavoie(2001-02)をベースにしていました。
しかし今回は、Godley and Lavoie: Monetary Economics(2014)等に載っているマトリクスを参考に、手計算可能レベルの非常に単純化したオリジナルのマトリクスを使用します。またそれにあたって複数のアドホックな仮定を設けています。(なので論理的におかしな箇所があるかもしれないので、発見された方はコメント欄に…)

「Pure Credit Economy」という仮定より、家計&企業のバランスシート上にはHigh Powered Money(HPM)は存在せず、民間銀行のみに存在します。
さて、前回の民間のみのマトリクスまでは「家計の預金=企業の当座借り越し」という関係性が成り立っていましたが、統合政府債(HPM)が導入されたことにより、その対称性はなくなります。家計預金は、企業の当座借り越しと、統合政府債の和に等しくなります。
この系においてMM定理(Modigliani–Miller Theorem)は成立しません。

銀行は受動的で潤滑油的な役割程度に落としています。というのも、ここで利鞘を導入して銀行に利益を稼がせても、非常に限定的な形にしかなりませんし、フローがめんどくさくなるからです。そのため銀行は利潤を稼がず、税金を払いません。租税は家計と企業から徴収されます。
銀行は利潤を稼がないという仮定上、「利息・利払い」から来る「支出・収入」のフローは一致するよう利子率(利回り?)は調整されます。ここでは、常に総預金利息フローと同じになるように利子率を調整するとします。
次に配当フローに関してですが、ここでは一定の配当利回りを仮定し、総和株価値と配当率の積を配当フローとしています。
株価値の決定、家計の富、フローの基礎づけ、貯蓄関数の導出
トランザクションマトリクスには、大体の文字の定義とフローの関係性が載っていますが、ここではマトリクス上省略されている関係性を明示的に示します。
GDPと三面等価の定義
$$
\bold{Y=WL+R+T}
$$
$$
\bold{Y=C+I+G}
$$
$$
\bold{Y=pq}
$$
$${Y=国民総所得、W=一人当たりの名目賃金、L=雇用数}$$
$${R=総利潤、T=総税収、p=価格、q=実質生産量、C=消費、I=投資、G=政府支出}$$
マクロの変数と比
$${資本蓄積率(g)=\frac{I}{K}、利潤率(r)=\frac{R}{K}、資本係数(V)=\frac{K}{Y_{fc}}、稼働率(u)=\frac{Y}{Y_{fc}}、Y_{fc}=最大生産}$$
$${預金・資本ストック比率(ξ)=\frac{D}{K}、負債・資本ストック比率(l)=\frac{B}{K}、τ=税率}$$
$${内部留保(P_n)=(R-i_{l}B-i_{s}PS)、配当収入(P_d)=i_sPS}$$
$${政府支出・資本ストック比率(β)=\frac{G}{K}、純利益率(π)=\frac{r_nV}{u_n(1-\tau)}、目標利潤率=r_n、目標稼働率=u_n}$$
株価の決定と家計の消費行動の詳細
ここでは行為主体の行動と、いくつかの仮定を再確認しておきましょう。
銀行は利潤を稼がないという仮定上、預金金利収入と当座借越金利収入は同値になる必要があります。したがって$${i_dD=i_lB}$$となります。
家計は収入と現状の預金から消費を行い、富の保持は預金もしくは株式の二択となります。よって貯蓄&消費性向と流動性選好&ポートフォリオ(富の保持割合)は以下の通りに表されます。
$$
\bold{c_h+s_h=1}
$$
$$
\bold{k_dV_h=D}
$$
$$
\bold{(1-k_d)V_h=PS}
$$
ここで総株価値は預金と流動性選好の関数と考え、表現します。すると上記の式より、総株価値は$${PS=D\frac{1-k_d}{k_d}}$$と表現できます。
このような定義によって、なぜ今回新規株式発行を考慮しないかを説明できます。なぜなら総株価値は預金と流動性選好の関数である為、株式発行部数の増加は株価の下落によって相殺され、預金と流動性選好に変化がない限り総価値は不変だからです。
では上記より、消費は以下の様に定義されます。
$$
\begin{array}{}C&=&c_h(WL+P_d+i_dD_{t-1}+i_sPS+D_{t-1})\\&=&c_h\Big(Y(1-\tau)(1-\pi)+D_{t-1}+D_{t-1}(i_d+i_s\frac{1-k_d}{k_d})\Big)\end{array}
$$
消費を定義する事ができたので、預金変化量も定義し直すことが出来ます。(式にある流動性選好と利回りの積が少し邪魔なので$${\alpha=i_d+i_s\frac{1-k_d}{k_d}}$$)と置いて、簡単にします)
$$
\begin{array}{}\Delta D&=&s_h(WL+P_d+i_dD_{t-1})-c_hD_{t-1}-T_h\\&=&(s_h-\tau)(Y(1-\tau)(1-\pi)+\alpha D_{t-1})-c_hD_{t-1}\end{array}
$$
投資フローと貯蓄関数
さて上記で定義し直したフローの式を基に、事後的な投資フローを稼働率と預金・資本ストック比率$${\zeta=\frac{D}{K}}$$の関数として描きましょう。
投資はトランザクションマトリクスより、以下の様に表現されます。(Remenber!!!$${\alpha=i_d+i_s\frac{1-k_d}{k_d}}$$)
$$
\begin{array}{}I&=&\Delta B+P_d\\&=&R-\alpha D_{t-1}+\Delta D-\Delta H\\&=&(1+\tau)(Y\pi(1-\tau)-\alpha D)+s_h(Y(1-\tau)(1-\pi)+\alpha D_{t-1})-c_hD_{t-1}-G\end{array}
$$
これは事後的に観察される関係性で、上記の式を$${K_{t-1}}$$で割り成長率($${g^{s}_{t}}$$)にします。上付き文字の[s]は貯蓄(saving)を表し、事後的な貯蓄と投資の一貫性を表す式ゆえに、$${g^{s}_{t}}$$で表される稼働率を関数とする式を貯蓄関数といいます。
したがって貯蓄関数は以下の様に表されます。↓
$$
g^{s}_t(u_t,\zeta_{t-1},\pi)=\frac{u_t}{V}\Big(s_h(1-\tau)(1-\pi)+\pi(1-\tau^2)\Big)-\zeta_{t-1}\Big(\alpha(c_h+\tau)+c_h\Big)-\beta
$$
貯蓄関数は3変数関数として表せることが出来ます。稼働率、預金資本ストック比率、利潤シェア割合(純利益率)の三つですね。
実際に分析する時は「短期→中期→長期」の順で「稼働率→預金資本ストック比率→利潤シェア割合」の順番で変数が変わっていくので、分析期間によっては定数として処理します。
これにてモデルの基本的な構造と骨格を作り終えました。あとは投資関数の導入です。
投資の内生化、投資関数について
この世界にはたくさんの投資関数がありますね、ハロッド=置塩型投資関数に然り、加速度原理、Ndikumana型等々…
今回はポストカレツキアンで一般的なBhaduri&Marglin型をベースとして改変したモノを使用します。
また改変に伴い、Bhaduri&Marglin型の使用に関する正当化も行います。
結論から入ってしましましょう、これが今回使用する改変Bhaduri&Marglin型投資関数です。↓
(γは反応性を表し、下付き文字は何に対する反応性か?を示しています。
例:$${\gamma_u}$$であれば、稼働率に対する反応性という意味です。また予測稼働率$${u^e}$$は例外的に上付き文字がついています。累乗と間違えないようお気を付けください。最後に、「t」は時間を表します。)
$$
\bf g^{i}_t(u^e_t,\zeta_{t-1},\pi)=(u^e_t-u_n)\gamma_u+\pi\gamma_{\pi}+\zeta_{t-1}\gamma_{\zeta}
$$
こちらも貯蓄関数同様に3変数関数です。唯一明確に違うのは「稼働率」ではなく「予測・期待稼働率」という変数を用いています。
またこの投資関数には一般的なBhaduri&Marglin型投資関数にはない預金・資本ストック比率($${\zeta=\frac{D}{K}}$$)が投資に対して正の影響を与えるように組み込んでいます。これに関しての正当化をしてみましょう。↓
Financial RatioとBhaduri&Marglin型投資関数の有効性
Financial Ratioは財務諸表内から選択した特定の値達の比を指します。
有名どころで言えば「RoA(利潤率)、Profit Margin(粗利…純利…等々)、Retention ratio(内部留保率)、debt ratio(負債比率), etc…」といった値です。
こうした「値」は三面等価というフローだけに着目した視点では、利潤率や純利といった概念は表現できますが、ストックが含まれる値は表現できません。
しかしストックフロー一貫アプローチに基づき、バランスシートマトリクスとトランザクションマトリクスによって経済システムを形作る事により、このような金融的・貨幣的側面を表現できるようになります。
実際に幾つか代表的なFinancial Ratioを紹介します。
(Remember! $${V=資本係数=\frac{K}{Y_{fc}}}$$)
RoA(利潤率)$${=\frac{税引き後純利益}{総売り上げ高}=\frac{u\pi(1-\tau)}{V}}$$
RoE$${=\frac{税引き後純利益}{自己資本}=\frac{Y\pi(1-\tau)}{V_f+D_t(\frac{1-k_d}{k_d})}}$$
Debt Ratio$${=\frac{総負債}{総資産}=\frac{B_t+D_t\frac{1-k_d}{k_d}}{K_t}}$$
Devident payout ratio$${=\frac{配当}{税引後当期純利益}=\frac{V(i_s\zeta_{t-1}\frac{1-k_d}{k_d})}{u\pi(1-\tau)}}$$
Interest cover ratio $${\frac{税引前当期純利益}{総利払い}=\frac{u\pi}{V\zeta_{t-1}i_d}}$$
等々……
他にも多数のFinancial Ratioは存在しています。上記から見て取れるよう、SFCAを採用したことによりFinancial Ratioをマクロレベルでも表現できるようになっています。
そして着目すべきは、多くのFinancial Ratioを「稼働率(=u)、純利益率(=π)、預金(=D)」の関数としてマクロレベルでは描けることです。
Financial Ratioは必ず全ての企業の財務諸表内に記載される、株主や経営陣にとって非常に重要な意思決定の材料です。当然、将来における意思決定に深くかかわっています。
例えば、Devident payout ratioは株主にとって重要な指標の一つです。
これは税引き後当期純利益の内、何割が配当に成ったかを表す指標であり、配当を払う企業であれば、この割合は3割~5割がミクロで適切とされます。
低すぎれば、利益のわりに配当を出さない企業として見られ、株式の購入に影響が出るでしょう。
次にInterest cover ratio です。これは企業の健全さを表す指標の一つであり「負債への利払いが、どれだけ営業利益でカバーできているか?」を表す指標です。ミクロでは最低2以上が健全か否かの条件となります。
このように、Financial Ratioは株主・経営陣の意思決定に深くかかわっており、これらが投資に影響を与える事は想像に難くありません。
ではこれらを表現する時、いちいち各Financial Ratioと投資への影響を持たせるよりも、これらFinancial Ratioに共通する”変数”を投資と関係させる方がはるかに簡単で適切です。
そして、これらFinancial Ratioをマクロで見たときに多く共通する変数は「稼働率(=u)、純利益率(=π)、預金(=D)」です。
したがって、ここで使用されるBhaduri&Marglin型投資関が$${g^{i}_t(u^e_t,\zeta_{t-1},\pi)=(u^e_t-u_n)\gamma_u+\pi\gamma_{\pi}+\zeta_{t-1}\gamma_{\zeta}}$$
となるのは、おかしくないといえるでしょう。
行為主体の意思決定と合理性
Bhaduri&Marglin型投資関数における$${\pi\gamma_{\pi}}$$が表すのは、企業が客観的に現状認識している自身の純利益率と、それに関連するFinancial Ratio達の評価と投資への反応性です。
(つまり企業サイドの視点)
次に$${\zeta\gamma_{\zeta}}$$が表しているのは、家計が現状認識している自身の純資産の量と投資への反応性です。なぜ預金でなく純資産かというと、先に定義したように株式は預金の関数として描けるためです。
(つまりこれは家計サイドの視点)
では稼働率の項は何を表しているのでしょうか?
$${(u^{e}_t-u_n)\gamma_u}$$が表すのは、行為主体が通常だと認識しているFinancial Ratioと、現状の彼らの予想・期待Financial Ratioを参照&比較し投資を決定している。ということです。(つまり家計&企業の視点が入っている)
注意として、ここでは主観的な稼働率に対する評価の重み付けが等しくなっています。これは行為主体の主観的意思決定を単純な形で表現するためであり、実際は$${u^e>u_n}$$と$${u^e < u_n}$$に対する絶対的評価は非対称になっているべきと思われます。

これは行動経済学のプロスペクト理論といわれる部分に関わるもので、行動経済学の代表的な理論です?(話半分で見てください)
では上記の事柄がどのように投資関数と関係するかを軽くだけ…
先に述べたとおり、この投資関数における稼働率の項は家計と企業、両者の視点を代表していると書きました。企業は財務諸表を作成しなければなりませんから、株主はもちろん利害関係者全員が目を通し、そうして時期の投資量が決定されます。
ではこの時、予測している財務状態よりも悪いならば、全体として投資へのネガティブな圧力が働くことは容易に想像できますし、逆も然りです。
Steven Hailの「Economics for Sustainable Prosperity 」にて紹介されている、標準的な価値関数(ここでは$${v(u^e)}$$とする)を用いて、この意思決定を表してみましょう。
正の範囲($${u^e>u_n}$$)では、価値関数は$${v(u^e)=(u^{e} - u_n)^a}$$となり、負の範囲$${u^e < u_n}$$では$${v(u^e)=-\lambda (u_n-u^e)^b}$$と表現します。(a、bは1以下、ラムダは損失回避係数)
次にプロスペクト理論の二つ目の柱である「確率加重関数」です。
確率加重関数は、価値関数によって求まる価値にその価値が実際に起こる確率をかけたものの合計を最大化するよう、意思決定を行います。この確率は客観的な物ではなく主観的に歪んでおり、小さい確率をより過大評価し、大きい確率を過小評価するようになっています。
ではこの文脈における”その確率”は「予測した稼働率が現実として実際に観察される稼働率とあっている確率」といったモノになるのではないかと思います。(しらんけど)
よってもしBhaduri&Marglin型投資関数をプロスペクト理論で基礎づけた場合、行為主体は前期に観測された稼働率$${u_t}$$を基に稼働率を予測し、これは価値関数$${v(u^e)}$$によって評価され、評価された価値に主観的な確率がかけ合わさり実際の投資量が決定されます。
しかし!!!!!!
こんな面倒くさい工程を入れ込むと簡単に解けなくなってしまうので、非常に簡易的に行為主体の主観的な意思決定を入れ込むために$${(u^e-u_n)\gamma_u}$$と表現しました。(書いてから思ったけど、この話いらんくね?)
【短期均衡】Financial Ratioを固定、期待と予測の完成まで分析
導入した貯蓄関数と投資関数を横軸が稼働率、縦軸を資本蓄積率としたグラフ上にケインジアン安定条件$${s_h(1-\tau)(1-\pi)+\pi(1-\tau^2)>V\gamma_u}$$が満たされているなら、以下のような図を描くことが出来ます。
青い線が貯蓄関数
$${g^{s}_t(u_t,\zeta_{t-1},\pi)=\frac{u_t}{V}\Big(s_h(1-\tau)(1-\pi)+\pi(1-\tau^2)\Big)-\zeta_{t-1}\Big(\alpha(c_h+\tau)+c_h\Big)-\beta}$$
を表し。
赤い線が投資関数$${g^{i}_t(u^e_t,\zeta_{t-1},\pi)=(u^e_t-u_n)\gamma_u+\pi\gamma_{\pi}+\zeta_{t-1}\gamma_{\zeta}}$$を表します。

預金資本ストック比率を定数として扱い、期待と予測が完成するまでを扱います。
さて、仮に均衡稼働率$${u^*}$$ではない地点に経済がいると考えましょう。
投資は予測・期待稼働率を以てして決定され、行われた投資は現実の稼働率として現れます。現れた稼働率より、行為主体は期待と予測の修正を行い、次期の投資を決定します。
先ほどのグラフでは、以下の様に表現できます。
期待稼働率①より投資の決定、事後的関係性として現れる投資と稼働率の組み合わせは貯蓄関数上に実現し、行為主体はその情報より自らの期待・予測稼働率を修正、次期の投資を決定します。

ケインジアン安定条件が満たされている時、上記のプロセスが何度も行われるにつれて期待・予測稼働率は現実の稼働率と等しくなっていきます。
最終的に$${u^e_t=u_t}$$となる時、それを均衡稼働率$${u^*}$$といい、期待が完成されています。
$$
u^e_t=u_t=u^*=\frac{V(\pi\gamma_{\pi}-u_n\gamma_u+\beta+\zeta\gamma_{\zeta}(\alpha(c_h+\tau)+c_h))}{s_h(1-\tau)(1-\pi)+\pi(1-\tau^2)-V\gamma_u}
$$
短期的パラメーターの変化と影響
では、短期における貯蓄性向や流動性選好といったパラメーターが与える短期的影響を紹介します。
まず貯蓄性向の増加です。貯蓄性向の増大は貯蓄関数の左回転、および上方シフトを引き起こし、稼働率、成長率共に低下させます。
ごく初歩的なケインズモデルで観察される貯蓄のパラドクスが成立していますね。

次に流動性選好の変化です。
株式を資産として保持したい欲求が高まった場合、それはどのようなマクロ的変化を引き起こすでしょうか?↓

株式をより多く保有しようとする行動は($${k_d}$$)の低下として表現できます。
これは貯蓄曲線を右シフトさせ、稼働率、成長率共に押し上げます。
(余談ですが、預金利子率や配当利回りが増加した場合も同様の事柄が発生します)
また背後では株式市場の高騰が発生しており、企業の市場評価値(トービンのqなど)が高まっているでしょう。同時にマクロレベルでの配当支払いフローは増加します。
短期における賃金or利潤主導レジーム
期待・予測稼働率が現実の稼働率と一致している時、純利益率の関数として成長率を描くと以下のような曲線が現れます。

さて、成長率を純利益率の関数として書いた$${g(\pi)}$$の一階微分地点より左側が賃金主導レジーム、右側が利潤主導レジームを表しています。
価格は長期までは固定と仮定しているため、この時の純利益率の変化は労賃から来るものであり、これは労働コストの上昇・低下が最終的な投資に与える影響を表しています。
上記のグラフより、一階微分ゼロ地点が負の領域にある可能性、もしくは一階微分ゼロ地点が存在しない可能性もあります。
ではどのような時に賃金主導経済は第一象限により多く表れてくれるでしょうか?
それは大体「消費性向が高い場合、株式の保有欲が大きい場合、負債、株式への利回りが大きい場合」の3パターンとなります。
また注意すべき事柄として、労働分配改善からくる利潤低下(=投資減少)は稼働率(=総生産)の低下と同義ではないことです。
利潤低下が稼働率に負の影響を与えるか否かを判断するには、均衡稼働率を純利益率の関数と取った、それの一階微分が正か負かで判断可能です。
つまりは$${\frac{\partial u^*}{\partial \pi}}$$が正の場合は利潤低下は負の影響、負であれば利潤低下は稼働率に正の影響。
また$${\frac{\partial u^*}{\partial \pi}}$$は必ずゼロ以下orゼロ以上のため、正と負の反転は純利益率以外のファクターが存在しており、それは偏に貯蓄性向です。
貯蓄性向が非常に高いとコスト増加は負の影響を与え、低いと正の影響を与えます。したがって費用の逆説(コストのパラドクス)が成立するためには、貯蓄性向は低くなければなりません。
小話:短期とは、時間にしてどれくらい?
短期、とはいうものの…現実の分析としてストックを所与とし、稼働率の調整を論じる時、実際はどれほどを短期とみなすべきなのでしょうか?
これに関して、つい最近でたワーキングペーパーが論じていました。それはEttore Gattoの”How short is the Short run in the Neo-Kaleckian Growth Model?(October 2021)”です。
結論としてはおおよそ2年程度とみなせるそうです。またケインジアン安定条件が調整速度に深くかかわっている事が指摘されました。
これは上記のモデルでも確認できて、貯蓄性向が低いほど調整回数をより多く要求するため、時間がかかります。
【中期均衡】Financial Ratioの定常状態の分析
短期均衡が常に達成されているという条件の下で、預金資本ストック比率を変数として扱い、その定常状態を探ります。
預金資本ストックの変化率と、その方向を求めましょう。
預金資本ストックの変化率$${\zeta=\frac{D}{K}}$$を対数で取って時間で微分しましょう。すると$${\hat{\zeta}=\hat{D}-g}$$となります。
成長率(g)は貯蓄関数より、すでに分かっていますので、預金の変化率を求めましょう。
預金の変化率は、預金変化量の式を$${D_{t-1}}$$で割れば
$${\hat{D}=(s_h-\tau)(\frac{u^*(1-\tau)(1-\pi)}{V\zeta}+\alpha )-c_h}$$と表せます。
資本蓄積率、預金変化率共に稼働率と預金資本ストック比率の関数として描けています。また短期均衡が常に達成されているため、均衡稼働率は$${u^*(\zeta)}$$の様に預金資本ストック比率の関数と記述できるため、一変数関数として横軸を$${\zeta}$$、縦軸に$${g(\zeta),\hat{D}(\zeta),\hat{\zeta}(\zeta)}$$を取ったグラフに図示する事が可能になります。
では$${\hat{\zeta}}$$が$${0}$$になる地点が長期的な調整が完了している地点ですので、実際に表してみましょう。
(グラフ内にある矢印は、調整の方向を表します)↓


さて定常状態がある場合は、上記の二つのパターンが存在しています。第一象限で安定的な一つの解が存在しているパターンと、第一象限に不安定な均衡点と安定的な均衡点の二つが存在するパターンです。
パターン①②共に預金の増加(=企業の借り入れ+政府債務)は成長を押し上げます。
ですが①では、預金の増加率は増えるにしたがって下がっており、これは間接的に、背後で起きている企業の負債増加or&政府負債増加の速度が減衰していく事を示しています。つまり負債が負債を呼ぶレジームでは”ない可能性が高い”ということであり、したがってこのパターンでは負債抑制レジームが発生している可能性が高いでしょう。
パターン②では、預金資本ストック比率の増加が自己実現的に増加速度を早くしていきます。よって背後では、企業負債と政府債務の増加の連鎖が起きているといえます。これは負債が新たな負債を呼ぶレジームとして、負債主導レジームが発生している可能性が高いと言えるでしょう。
中期均衡の実数解
今の所グラフィカルな形で紹介しましたが、これを実際に解いてみましょう。
$${\Delta \zeta =\hat{D}\zeta-g\zeta}$$は変化量を表しており、これが=0となる点が長期均衡ですので、実際に代入してみましょう。
$$
0=(s_h-\tau)(\frac{u^*(1-\tau)(1-\pi)}{V}+\alpha\zeta_{t-1} )-c_h\zeta_{t-1}-\frac{u^*\zeta_{t-1}}{V}\Big(s_h(1-\tau)(1-\pi)+\pi(1-\tau^2)\Big)+\zeta^2_{t-1}\Big(\alpha(c_h+\tau)+c_h\Big)-\beta\zeta_{t-1}
$$
これは$${\zeta}$$に対する二次関数なので、解の公式を使って実数解を求める事が出来ます。
したがって解は↓
$$
\zeta^*=\frac{-\left(\left(s_h-\tau\right)\left(\frac{\left(\gamma_{\zeta}+\alpha\left(c_h+\tau\right)+c_h\right)\left(1-\tau\right)\left(1-\pi\right)}{\left(s_h\left(1-\tau\right)\left(1-\pi\right)+\pi\left(1-\tau^{2}\right)-V\gamma_{u}\right)}+\alpha\right)-c_h-\frac{\left(\pi\gamma_{\pi}-u_{n}\gamma_{u}+\beta\right)\left(s_h\left(1-\tau\right)\left(1-\pi\right)+\pi\left(1-\tau^{2}\right)\right)}{\left(s_h\left(1-\tau\right)\left(1-\pi\right)+\pi\left(1-\tau^{2}\right)-V\gamma_{u}\right)}+\beta\right)-\sqrt{\left(\left(s_h-\tau\right)\left(\frac{\left(\gamma_{\zeta}+\alpha\left(c_h+\tau\right)+c_h\right)\left(1-\tau\right)\left(1-\pi\right)}{\left(s_h\left(1-\tau\right)\left(1-\pi\right)+\pi\left(1-\tau^{2}\right)-V\gamma_{u}\right)}+\alpha\right)-c_h-\frac{\left(\pi\gamma_{\pi}-u_{n}\gamma_{u}+beta\right)\left(s_h\left(1-\tau\right)\left(1-\pi\right)+\pi\left(1-\tau^{2}\right)\right)}{\left(s_h\left(1-\tau\right)\left(1-\pi\right)+\pi\left(1-\tau^{2}\right)-V\gamma_{u}\right)}+\beta\right)^{2}-4\left(\left(\alpha\left(c_h+\tau\right)+c_h\right)-\frac{\left(\gamma_{\zeta}+\alpha\left(c_h+\tau\right)+c_h\right)\left(s_h\left(1-\tau\right)\left(1-\pi\right)+\pi\left(1-\tau^{2}\right)\right)}{\left(s_h\left(1-\tau\right)\left(1-\pi\right)+\pi\left(1-\tau^{2}\right)-V\gamma_{u}\right)}\right)\left(\frac{\left(\pi\gamma_{\pi}-u_{n}\gamma_{u}+\beta\right)\left(1-\tau\right)\left(1-\pi\right)\left(s_h-\tau\right)}{\left(s_h\left(1-\tau\right)\left(1-\pi\right)+\pi\left(1-\tau^{2}\right)-V\gamma_{u}\right)}\right)}}{2\left(\left(\alpha\left(c_h+\tau\right)+c_h\right)-\frac{\left(\gamma_{\zeta}+\alpha\left(c_h+\tau\right)+c_h\right)\left(s_h\left(1-\tau\right)\left(1-\pi\right)+\pi\left(1-\tau^{2}\right)\right)}{\left(s_h\left(1-\tau\right)\left(1-\pi\right)+\pi\left(1-\tau^{2}\right)-V\gamma_{u}\right)}\right)}
$$
となり、解が求まりました。
ちなみに、この厳密解が実数解でなく虚数になってしまう場合、それは
負に無限大に発散している状態を表します。↓

パラメーターが与える定常状態への影響
厳密解が求まったことにより、中期均衡がどのように変化するかを調べられるようになりました。
先ず、上記のグラフは変化率を縦軸に表示していますが、変化量で取ってみるときれいな二次関数が現れます。(当たり前だが)
二次関数は基本パターン①でもパターン②でも上に凸です。
ただパターン1の場合、x軸と交わる点の一つは負になってしまうため、経済学的に意味ある解となりません。
以下図

利子率が上昇する時、貯蓄性向が高まるとき、株式保有性向が増える時、税率が下がるとき、Δζの曲線は右上方シフトを引き起こし、均衡点は両方増大します。以下の様に図示できるでしょう。
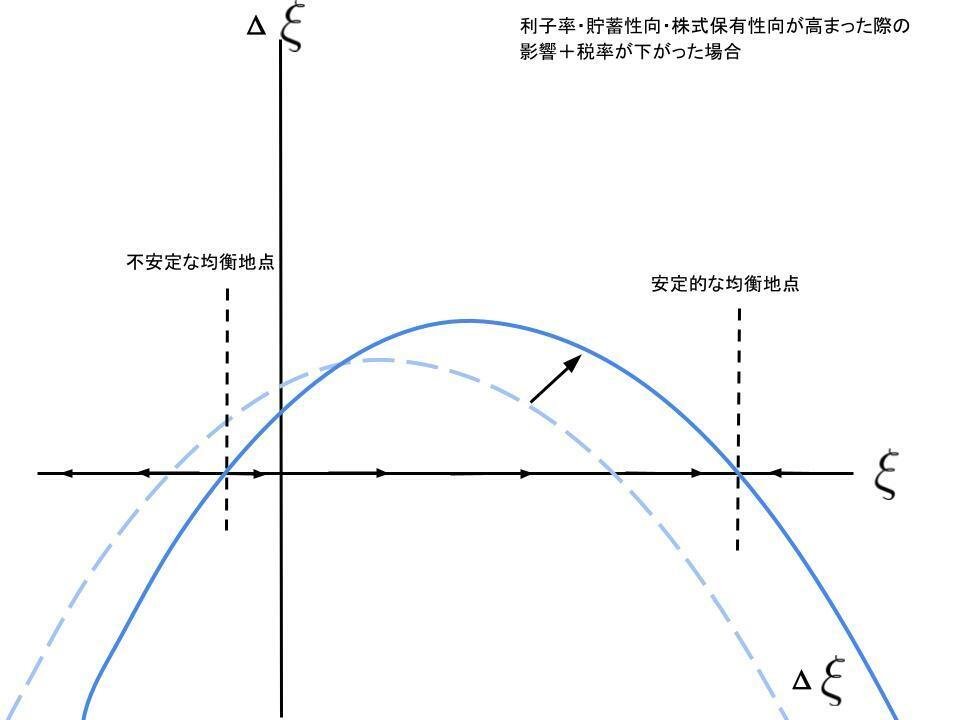
では、政府支出が増えた場合の挙動を見てみましょう。「政府支出が増える」つまりここで言う、対最大GDP比政府支出が恒久的に増加する場合。中期的な影響はΔζ曲線の上方シフトを引き起こし、両方の均衡点が外側にシフトします。
この時、状況によっては元々第一象限にいた不安定な均衡点が負の領域へ入ってしまうかもしれません。つまりそれはパターン②の状態にあった経済がパターン①へ変化したことを表します。

比較動学:中期的な資本蓄積率と均衡稼働率
ではこれら預金資本ストック比率変化が投資と均衡稼働率に与える中期的影響を見てみましょう。
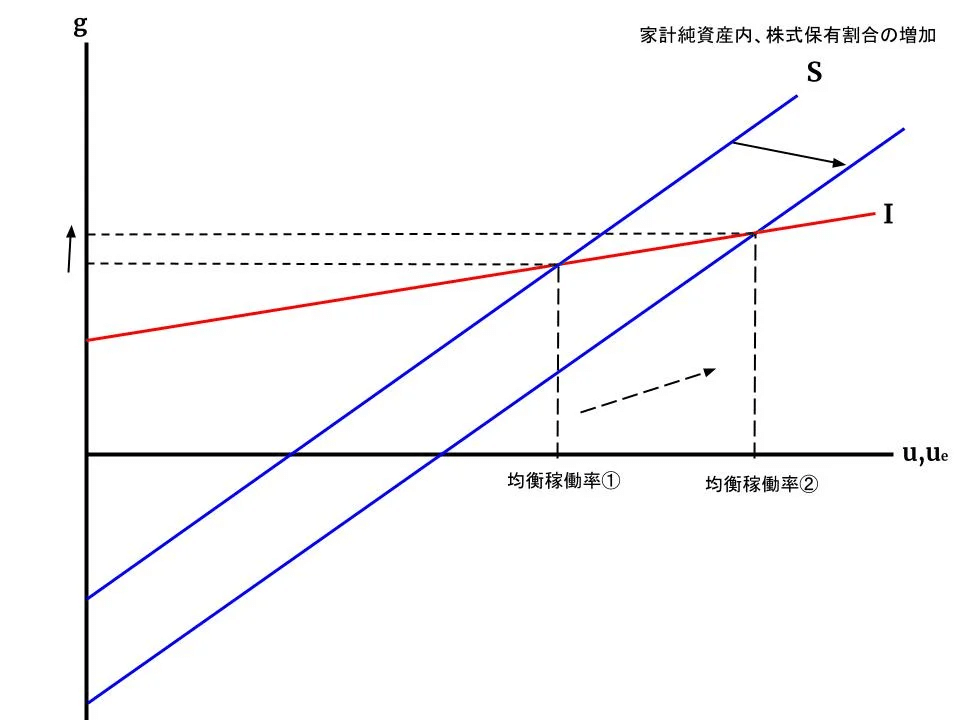
例えば貯蓄性向の上昇は、短期においては以下のような事象を観察できました。↓

上記の図から見て取れるように、ネガティブな影響を見せます。しかし、中期的な影響として貯蓄性向の増加は貯蓄曲線の右シフトと投資曲線の上方シフトを引き起こし、稼働率&成長率共に押しあげます。↓

当然この背後ではInterest Cover Ratio, Devident Payout Ratio, etc…といったFinancial Ratioが上記の動きと追従した変化を見せます。
では次に、流動性選好の変化はどのような影響を与えるでしょうか?引き続き見ていきましょう。
まず短期では以下の様な動きが観察されました↓
次に中期では、先ほどすでに論じた通り、安定的な均衡預金資本ストック比率は上昇しているため、貯蓄曲線はさらなる右シフト、投資関数は上方にシフトを引き起こし、稼働率&成長率を押し上げます。
つまり貯蓄性向増大の時とは違って、短期においても、中期においても正の影響を与える事が分かります。
この様に、短期&中期共に正の影響を与えるパタメーターは幾つか存在していて「政府支出、利子率の上昇、配当利回りの上昇、株式保持性向の増大」です。
強調してはいませんが、利子率、というよりこの場合は預金利回り・当座借越し利回りの増大は短期においても中期においても成長率と稼働率を増大させます。これは利払いを含むポストカレツキアンモデルにてよく観察される現象です。
ちなみに…
上記は比較動学ですので、安定な均衡状態に速やかに調整される事を仮定しています。ただ実際は時間の経過と共にそれらは達成される訳ですから、時間を横軸に取ったグラフで、その過程のイメージ図を大雑把に示しておきます。

先に書いた通り、貯蓄性向が上昇するというショックが起きた場合、短期均衡稼働率は低下し、中期的には回復してゆきます。
中期における賃金or利潤主導レジーム
価格水準・分配率の変化が与える影響を見ていきましょう。
中期均衡地点$${u^{**}}$$に経済が存在していると仮定して、先ほど同様「純利益率($${\pi}$$)」の関数として中期成長率$${g^{**}}$$と中期利潤率$${r^{**}}$$を見ていきましょう。

短期で見られた利潤率と成長率の関係とは、また違った関係性が見えます。
上記の図は、均衡成長率(g**)・利潤率(r**)を純利益率(π)の関数と取った時に、均衡預金・資本ストック比率(ζ*)が発散するような純利益率(π)が、自然数に存在しない際に見られる形状の一種です。
短期と同じように$${\frac{\partial g }{\partial \pi}<0}$$の領域(賃金主導成長レジーム)と$${\frac{\partial g }{\partial \pi}>0}$$の領域(利潤主導成長レジーム)の存在が確認できます。ただし短期の場合とは違って、負の領域にまたがって曲線が存在していない。という違いがあります。
またほかにも利潤率の曲線は、短期に比べ異なる様相を呈しています。
利潤曲線(r**)には一階微分ゼロ地点が二つ存在しており、賃金主導レジーム$${\frac{\partial r}{\partial \pi}<0}$$は利潤主導レジーム$${\frac{\partial g }{\partial \pi}<0}$$の領域に挟まれるように存在しています。
加えて$${\frac{\partial g }{\partial \pi}=0, \frac{\partial r }{\partial \pi}=0}$$を満たす$${\pi}$$は同値でない可能性があります。
場合によっては「純利圧迫が総利潤を引き上げるが、投資は引き下げる(逆もまた同様)。」そのような経済状態が存在する可能性を示唆しています。
注意すべき点として、短期&中期共に$${u_n}$$は固定されているということです。つまり$${\pi}$$の低下は、目標利潤率($${r_n}$$)が諦められることで起きています。
また$${\frac{\partial u^{**} }{\partial \pi}<0}$$となるので、賃金主導型レジームにはインフレーションバリアの制約があります。そのため恐らく変曲点の後ろ側にある$${\frac{\partial r }{\partial \pi}=0}$$となる部分は実現不可能と思われます。↓

ふう…中期における成長と利潤の話を大方できたので、今度はもう少し視点を広げていきましょう。
いまから部門別純金融フローの話をした後、今まで所与としてきた通常稼働率($${u_n}$$)を内生化し、均衡稼働率と期待稼働率が通常稼働率と等しくなるまでの最終的な調整過程を分析します。
そのような最終的均衡ポジションにおいて、行為主体の期待は100%完成しており、$${r_n=r, u_n=u_t}$$を満たします。そして通常稼働率と現実の稼働率が同じになるような均衡稼働率を$${u^{***}}$$と表現します。
Godleyの視点:部門別純金融フロー分析
さて、MMT派の世界観に基づいた教科書「Macroeconomics by Wray Mitchell」でも登場する、非常に簡素ながら分かりやすい概念・モデルとして、ゴットリーの部門別バランスフレームワークがあります。
頻出する形は国民経済計算の式より導出されます。ここでは解釈の仕方を含めて簡単に紹介しておきましょう。
基本的な文字の意味
$$
S=貯蓄\\X-M=純輸出\\FNI=純海外収支\\CAB=経常収支\\GNP=国民総生産
$$
基本的な恒等関係
さてと、基礎的な式から始めましょう。
$${GDP=C+I+G+(X-M)}$$
これは国内総生産の恒等式です。
ですので、海外からの自国籍企業の収入等は入っていません。
そこで、これをGNPにします。
$${GNP=C+I+G(X-M)+FNI}$$
さらにここに税金を加えます。(企業の内部留保は無いと仮定する)
$${GNP-T=C+I+G(X-M)+FNI-T⇒(GNP-C-T)-I=(G-T)+(X-M+FNI)}$$
式の(GNPーCーT)が「S」を表します。
綺麗に書き直すと↓
$${(SーI)=(GーT)+(X-M+FNI)}$$
になります。
この際の(S-I)がプラスの場合は、民間は純金融資産を貯蓄していることになります。
マイナスの際は、民間は収入より多くの支出を行っており、それすなわち「資産」を切り崩している、もしくは、負債を発行しているという事になります。(これはフローの話です)
さて(X-M+FNI)は(CAB)に変換が可能です。
$${(S-I)+(T-G)+(-CAB)=0}$$
この様に、すべての総計は必ず0になります。
では、簡単な図にしてみましょう。

半分より上は政府黒字、下は政府赤字。半分より右は経常収支黒字、左は経常収支赤字、左上は民間赤字、右下は民間黒字を表します。
これは財政スペースを表してもいます。経常収支というのは、自国では最もコントロール不可な部分です。もし、国が潜在的に経常収支赤字国である場合、上記の財政スペースは以下の様になるでしょう。

部門別バランスの問題上、財政スペースは上記の様にならざるおえません。
ではもしここで、この国が変動相場制でない場合、財政赤字にはある程度の限度が存在しています。その制約をここで表現してみましょう。↓
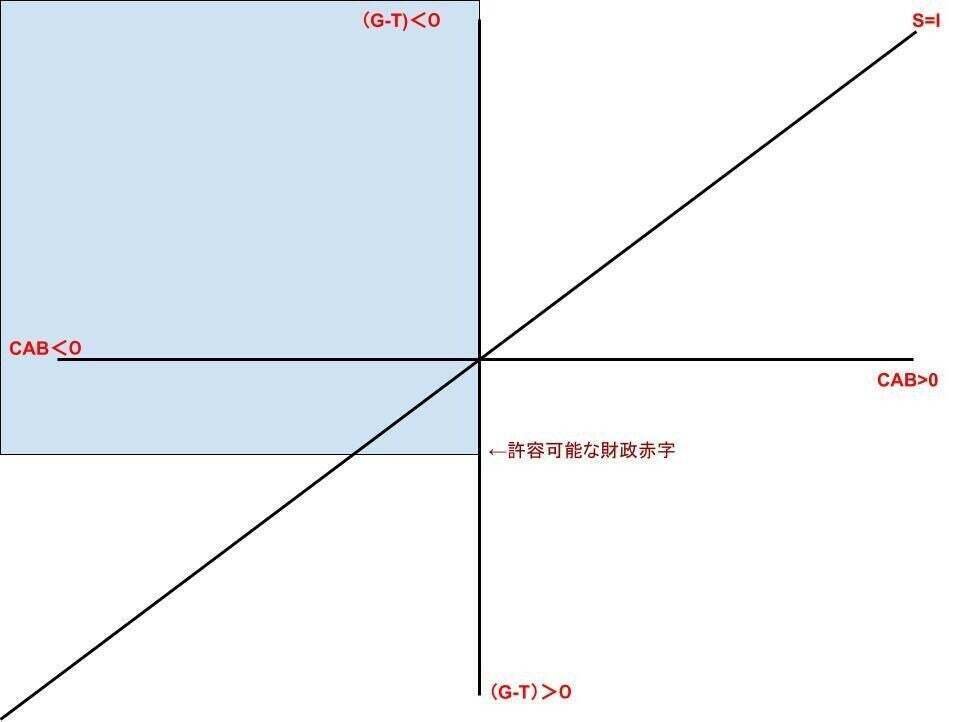
このように、財政スペースは著しく制約され、Ficial Policyにも多大なる影響を与えます。
上記のような状況の国家であれば、ほぼ民間黒字の可能性は望み薄でしょう。ここでもし政府が黒字である場合、民間は100%赤字を膨らましています。
これが長期的に安定的かどうかはここではわかりませんが、重要なのは、財政的制約が課せられたときに政府が操作しなければならない政策スペースは、主権を持つ通貨発行国の政府が利用できる選択肢に比べて非常に限られているという事です。
これはなぜ重要なのでしょうか?
制約のない政府は、総需要が完全雇用と物価安定を維持するのに十分であることを保証するために、常に利用可能なスペースを活用することができるからです。
定義上、すべての国が対外的に黒字を出せるわけではありません。なぜなら、ある国の対外的な黒字は、他の国の対外的な赤字と一致しなければならないからです。
もし先ほどの様に財政赤字に許容限度があるよう国では、許容される財政赤字が完全雇用を保つのに必要な総需要を維持する事が不可能な場合があります。
対外赤字を抱え、同時に特定の財政ルール下で運営しなければならない国が直面する政策の柔軟性のなさは、非常に致命的になりえるでしょう。
このような経済が、民間部門が支出を削減して黒字を目指すほどの大きな負の経済ショックを経験した場合、全体の総需要の損失を吸収するために財政赤字を利用できる範囲は非常に限られているでしょう。
さて、このように部門別バランスアプローチは有益な視点を多数提供してくれます。しかしこれは「フロー」だけの話である事に留意してください、
では閉鎖体系ではありますが、政府部門込みカレツキアンで似たような表現をしてみましょう。
ストック変化量がGDPに占める割合を、稼働率の関数として表現します。トランザクションマトリクスより、簡単に式は求める事が出来ます。
グラフ上に図示してみましょう↓
部門別対GDP比純金融フロー

赤線が政府の対GDP比純金融フローで、青線が企業の対GDP比純金融フローを表し、緑線は家計を表しています。
これは先ほど”民間”として捨象されていた部分をより細かく書いています。一応の前提条件で「負債の発行主体は政府と企業である」としましましたが、企業が当座借越しをしない可能性も十分に考えられます。
実際にいくつか分析してみましょう。↓
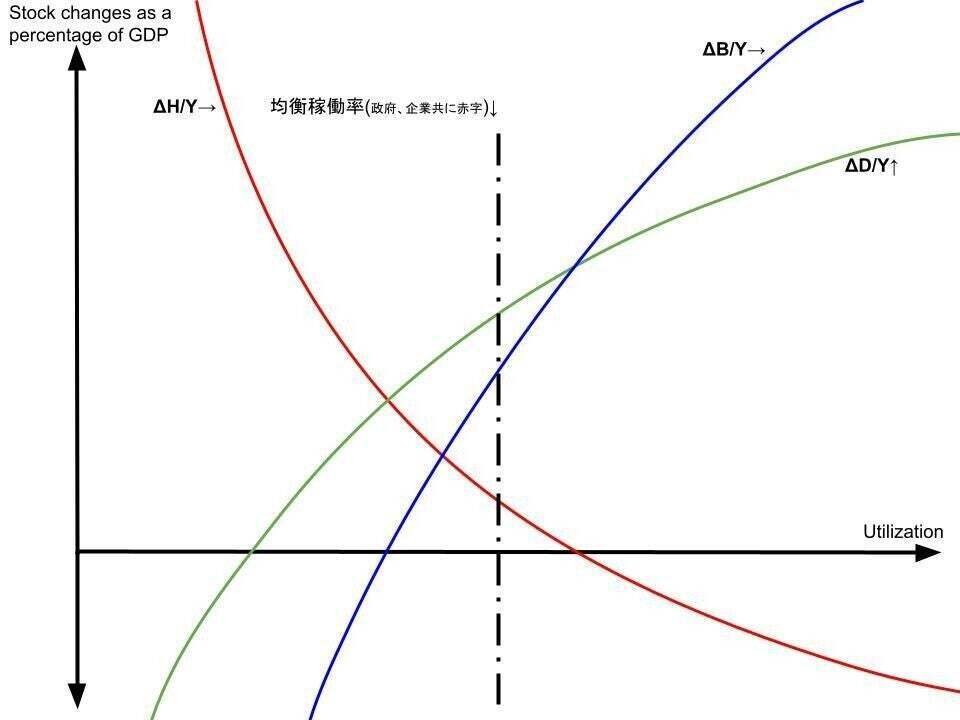
長期均衡稼働率が上記の地点にあるとしましょう。ビジネスは政府よりも多く負債を出しつつ、政府自身も負債を発行している状態です。
ではこの時、政府が黒字化を目指して大規模な支出削減を行った場合、短期的には以下のような動きがみられます。

政府が支出を減らしたため、当然短期稼働率は後ろに引き下がりました。また部門バランスの関係上企業がその埋め合わせを行う必要が出来ると同時に、家計預金のフローも減少しました。(シフトはしませんが)
対最大GDP比政府支出を恒久的に減らした場合、長期的な預金・資本ストック比率も減る事は前述の通りです。すると政府の対GDP比純フロー以外の曲線がシフトします。

この場合、結果として財政赤字に逆戻りしています。
さて、このゴットリーのバランスアプローチを介して見えるのは、マクロにおけるフローの一貫性に関する視点です。
「政府」という部門の追加によって、ビジネスが当座借越しを必要とするか否かは、政府支出&税率と家計の流動性選好&貯蓄性向の具合によって変化します。
事前に書いた通り、政府支出と税率は外生変数ですが、税収そのものは総所得の関数です。ではビジネスの支出はどうでしょうか?
彼らは支出に伴って必ず当座借越しを必要とします。いくらかは前期からの余剰金を使用して賄えますが、足りない場合はその分を新たに借り入れなければいけません。
ビジネスが借り入れる額は、彼らの”期待”と”現実”に大きく依存します。期待は”予測稼働率”の形で表現され、”現実”はその他のパタメータ達が表しています。
投資に先立ち、主体の手続き合理性に基づいた意思決定が存在し、生産に伴う借り入れが行われ、家計への分配が起こります、これが預金を生成し、家計も手続き的合理性に基づいて消費し、流動性選好が株式価値と企業価値を変動させるでしょう。
この時、政府の行動の変化は、彼らの観測する最終的な結果(稼働率)を変化させ次期の”予測/期待”を変移させます。政府支出の最大GDP比率が増える時、つまりは政府支出が増える時、これは民間の実現資本稼働率を押し上げ、彼らの予測を乱すでしょう。これは短期均衡の貯蓄式の右シフトとして表現できます。
長期的預金・資本ストック比率の均衡地点も引きあがり、政府支出の増加によって短期的な稼働率上昇+長期的にも稼働率が上昇するでしょう。
では「長期的に預金・資本ストック比率が大きく上がる」とはどのような工程を踏んで起こるでしょうか?
政府支出の増大が、短期的にビジネスの借り入れ量を減らしつつ、家計の預金量を増やしていきます。これは総株価値の増加を引き起こし、短期貯蓄曲線は右シフト、投資曲線は上方シフトしさらなに生産量と投資を増やすことになります(ここまで聞いていると”良い事”の様に聞こえますが、現時点では多数の制約が矮小化されている事に留意しましょう)
このように行為主体の行動の変化は、他の部門の純金融フローへ多大な影響を与えると共に、それらは経済の在り方自体を変える可能性を持っています。
もし政府黒字を望むなら、企業を莫大な赤字主体にする事を許容しなければなりません。現状が政府赤字+企業黒字の状態で、それほどのレジーム転換を試みる事がどれだけ混乱をもたらすかは想像に難くないでしょう。だからと言って何もしない事が”正解”とはなりませんが、”経済全体のバランス”への理解が無ければ有意義な議論も認識もできないでしょう。
小話:負債の量とインフレーションに関して
恒等式として、かならず$${\Delta D = \Delta B +\Delta H}$$となるのは既知の事柄ですが、上記の純金融フローの話より、これら変化量のどちらが大きいか?小さいか?が論じれるようになりました。
当然あり得るレジームとして$${\Delta B<\Delta D < \Delta H}$$などがあります。この関係性が満たされる場合、恒等式$${\Delta D = \Delta B +\Delta H}$$と$${D=B+H}$$より、企業の当座借越し増加量はマイナスになっている必要があり、それは企業が負債を減らしているor純資産をためている。と解釈できます。
また前提と中期均衡条件$${0=\hat{D}-\hat{g}}$$より、もし$${\Delta B<\Delta D < \Delta H}$$であるなら$${\hat{H}>g}$$($${g=\hat{Y}}$$)が成立していると言えるでしょう。
これが表すのは「政府負債成長率はGDP成長率・資本蓄積率よりも高い」ということです。
そしてそのようなレジームは往々にしてあり得る事であり、特段不安定なレジームではありません。政府負債は、GDP&資本よりも早い速度で上昇しますが、”その事実自体”がインフレーションを引き起こす事はあり得ません。
現状モデルに政府債務への利払いは入っていませんが、仮に入っていたところでこの結論が変わる事はありません。
【長期均衡】目標RoAが達成されるまでの分析
短期&中期と通常稼働率($${u_n}$$)を所与としてきましたが、これは株主やマネージャーに経営者といった主体が、その名の通り”通常”だと思っている稼働率です。そのため長期的にこれを実現させようと、彼らが何かしらのアクションを取る可能性は十分考慮に値します。
では中期均衡が成立している条件の下で、通常稼働率と現実の稼働率(中期稼働率)が一致しない時はそれを達成するように通常稼働率を変化させることで価格調整をする。と仮定しましょう。
ちなみにこのような調整方法は、ただの一例にすぎません。
ただこのアプローチは、「価格、分配、稼働率」という三つの変数を一つの式で調整させることが出来る上に、賃金主導レジームと利潤主導レジームが共存できる調整方法の一つであるため採用しました。
先人たちによっては、貯蓄性向の内生化や反応性を変化させるようなモデルを立てている人もいます。場合によっては賃金主導レジームが消えてしまったり、本質的に不安定なモデルになることもあります。
(Harrodian不安定性etc…)
今まで純利益率の変化が起きる時は、コストの上昇を転嫁せず、目標利潤率を下げたことによって起きていました。↓

つまりこれは賃金上昇($${\hat{W}}$$)から来るものでした。
しかし長期では、自身の望む通常稼働率に向けて通常稼働率を変化させることでマークアップを調整し、純利益率を調整します。↓
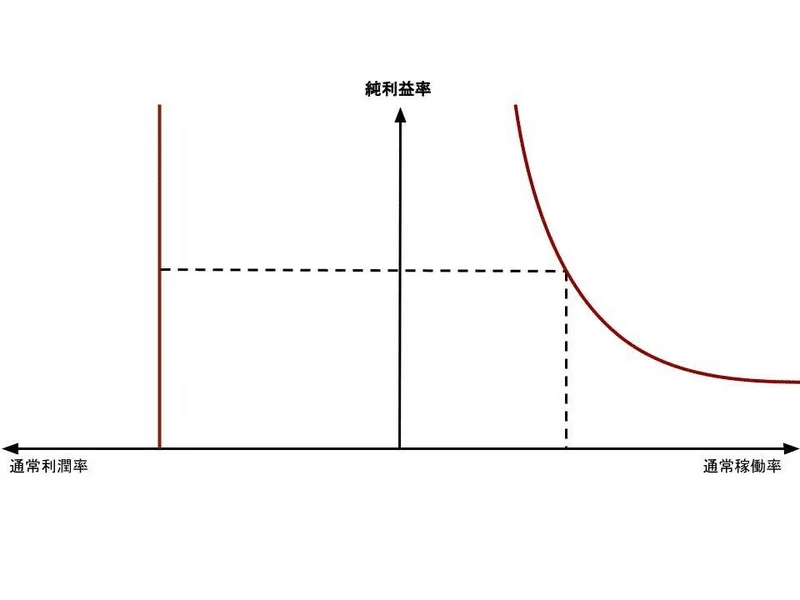
このような調整が可能なのは、前提で書いた通り、ターゲットリターン型プライジングを採用しているからです。
前提より、価格は$${P=(\frac{u_n(1-\tau)}{u_n(1-\tau)-r_nV})\frac{W}{y}}$$(yは一人当たりの生産性)であり、純利益率は$${\frac{r_nV}{u_n(1-\tau)}}$$ですね。
通常稼働率を内生化:長期均衡点と安定性
経済が通常稼働率に収束する事を保証するような”重力”はどこにもありません。そのため経営者や株主が”普通”と判断できる地点に経済がいるかどうかは未知数です。しかしもし、この”期待”が裏切られ続けているのであれば、今までの基準を変更し最適化を行おうとするはずです。
では企業が$${\Delta u_n=\phi (u^{**}(\pi)-u_n(\pi))}$$の様な形で調整を行うと仮定しましょう。(Φは調整速度を表す)
したがって最終的な調整ポジションは$${0=\phi (u^{**}(\pi)-u_n(\pi))}$$となる地点であり、そのような条件を満たす稼働率を長期稼働率$${u^{***}}$$と表します。
ではこれを実際に図示してみましょう↓

このように、$${\Delta u_n=\phi(u^{**}(\pi)-u_n(\pi))}$$が自然数の範囲で常に連続であるなら、以上のように図示できます。
実現可能で経済学的に意味がある解は二つ存在しています。不安定な方が賃金主導レジームで、安定的な方が利潤主導レジームに対応しています。
既知のとおり、賃金主導レジームは高い稼働率の元に成立し、低い純利益率はより高い預金・資本ストック比率をうみます。
したがって税収は比較的おおく、政府が発行するHPMは比較的少なく、場合によってはHPMを減らしているでしょう。くわえて部門別純金融フロー分析より、大きい預金資本ストック比率は、高い中期均衡稼働率と$${\frac{\Delta B}{Y}, \frac{\Delta D}{Y}}$$曲線の右シフトを引き起こします。
結果として企業は、より大きな赤字フローを作りだす、あるいは黒字を減らす、黒字主体から赤字主体に転換する、となるでしょう。
そのため、逆に経済が利潤主導レジームの場合であれば、企業は黒字主体である可能性が高く、政府が赤字主体になっているでしょう。
長期均衡が存在しないパターン
さきほほどは長期均衡が二つ存在し、かつ自然数の範囲で連続で、現実的な長期均衡の解が存在している場合における$${\Delta u_n}$$のグラフでした。
そうではないパターンも見ておきましょう。
例えば現実的な長期均衡の解が存在しないような場合です。

現実的な長期均衡の解が存在しないものの、関数は自然数の範囲で連続です。これは目標利潤率が低い時、貯蓄性向が高い時、株式への保有性向が高い時、貸付・配当利回りが大きい時etc…にみられます。一見すると、これでは長期的な解が無いため非現実的に見えるかもしれません。
このようなレジームでは、調整に従って純利益率の引き下げを行うものの、利潤と稼働率は増大を続けるため、調整がいつまでたっても終わりません。
しかし無限に通常稼働率を下げる事はできませんし、100%以上の稼働率を通常とみなすことはあり得ないでしょう。したがって100%近傍まで現実の稼働率が近づいた時点で、通常稼働率の調整は終了する事となります。
当然、調整は完成せず$${u_n=u_t}$$となっていませんし$${r_n=r_t}$$にもなっていません。
ではこれをさらに調整させるような行動を考えてみましょう。まずこのパターンにおいては$${r_n<r_t}$$となっている故に行為主体はより高い目標利潤率を志向する可能性が考えられます。すると今度は$${r_n=r_t}$$となるように$${r_n}$$を更新するかもしれません。もし$${r_n}$$が更新されより高い値に設定しなおされれば、これは$${\Delta u_n(\pi)}$$の式を下方シフト+$${\pi}$$を増加させるため、いずれ賃金主導レジームの均衡点に達した時点で調整が終わるでしょう。(かなり恣意的な調整方法である事に注意)

長期均衡は存在するが不安定な調整パターン
現実的な長期均衡の解が存在しながらも、特定の範囲で中期均衡が満たされな純利益率が存在する故に$${\Delta u_n(\pi)}$$が自然数の範囲で一部不連続になってしまうパターンです。
これは長期均衡が存在しない条件の逆で現れやすいです。(目標利潤率が高い、貯蓄性向が低い、預金への保有性向が高い、貸付・配当利回りが低い)

このパターンで厄介なのは、経済が賃金主導レジーム側の不安定な調整軌道に乗っている場合です。不安定な軌道で$${u_t< u_n}$$となっている場合は、調整過程で中期均衡が負に発散する領域に入ってしまいます。
ただ、このような不安定な軌道はそもそも存在できる位置にいない可能性がありますし、多少非現実的なパターンかもしれません。(しかし相対的政府支出・税収の大きさによっては現実的になる)
そのため、無難に上記のようなパターンを理解するとすれば、経済は$${\frac{\partial u^{**}}{\partical \pi}>0}$$を満たす領域に常におり、利潤主導レジームが解となる。といえるでしょう。
最後に:今回のモデルはDesmosで公開してます
これにて解析的ストックフロー一貫成長モデルの一例の紹介を終わりたいと思います。
今回は前提の説明から、その正当化に加えて、短期・中期・長期ごとに解の導出方法をお見せしました。まだまた掘り下げるべき部分は多数ありますし、分析の足らない箇所も多くあります。例えば、このモデルでは経済的な制約や不安定性に関しての視点が少ないです。賃金利潤フロンティアに自然成長率制約、インフレーションと産業予備軍効果といった代物ですね。
他にもミンスキー体制やスタインドル体制といったレジームへの言及も今回は省き、代わりに伝統的なカレツキアン視点のみを紹介したにとどまります。(なお昔の記事で多少紹介しました)
また「対GDP比政府支出」や「税率」といった特定のパラメーターが長期的な調整過程に与える影響に関する考察も省きました。
さらに人によっては、もっと気になる箇所や話題にしてほしかった部分もあるでしょう…
ですので!!!
今回のモデルはDesmosという無料のグラフサイトにて、皆さんが実際に触れるよう公開しておきます!!!!!!!!!!
リンク→https://www.desmos.com/calculator/a53gayeiq1
幾つかのラテン文字がDesmosでは使えないので置き換えてあります。
以下置き換えられた文字一覧⤵
$$
\pi\rightarrow M\\u_n\rightarrow u_0\\ \zeta^{*}\rightarrow Z\\ \zeta\rightarrow z \\ \gamma_u\rightarrow j_0 \\ \gamma_{\zeta}\rightarrow j_1 \\ \gamma_{\pi}\rightarrow j_2 \\ \alpha\rightarrow d\\ \beta\rightarrow q\\ \tau\rightarrow t\\ r_n\rightarrow r_0 \\ u^{**}\rightarrow U \\ \Delta u_n(\pi) \rightarrow L(x) \\ u^{**}(\pi) \rightarrow U_0(x) \\ \zeta^{*}(\pi)\rightarrow F(x)
$$
てーことで、実際に触って確かめてはいかがでしょうか??
きっと拙くてわかりずらい文章だったとは思いますが、ここまで読んでいただき誠にありがとうございました。
いつでもDMとかで質問してください!!あと間違いの指摘も!
Twitterアカウント→https://twitter.com/chibi_owo_suke
あとがき
今年一年間で学んだことを出来る限り詰め込んでみました。
高校三年の時に経済学にたまたま出会って、そこからハマって二年も続くとは思いませんでした。もしかしたらいつか唐突に飽きてしまうのかもしれません……でもこうして年末にもせっせと教科書を読んでるので、当分はハマっている気がしなくもない(笑)
冒頭で書いたとおり、SFCアプローチは本当に有用で、どんな世界観にも中立的なのに紹介されることはめったにないように思います。そもそも日本では数本程度しかSFC関連の論文が出ておらず、解析的なアプローチに限ってはほぼ皆無といっても差し支えないほどに紹介されません。
ですので学部一年として、より多くの同志に手に取りやすいモデルを紹介する事で、日本の死にかけ?で風前の灯火なPK界隈に少しは活気が戻せるんではないかと思い、記事を書いてみました。
兎に角、ちょっと変わった経済学への面白さが伝われば幸いです。
この記事が気に入ったらサポートをしてみませんか?
