
時系列分析入門【第5章 その3】時系列クラスタリング・再帰定量化分析・VARモデル・グレンジャー因果性検定・インパルス応答関数をPythonで実践する
この記事は、テキスト「RとStanではじめる 心理学のための時系列分析入門」の第5章「時系列データ同士の関係の評価」のRスクリプトをお借りして、Python で「実験的」に実装する様子を描いた統計ドキュメンタリーです。
取り扱いテーマは複数の時系列データを用いる以下のトピックです。
・時系列クラスタリング
・再帰定量化分析
・グレンジャー因果性検定
・VARモデル
・直交化インパルス応答関数
時系列てんこ盛りです!しかも波乱万丈!(波乱含みということ)
さあ、時系列分析を楽しんでいきましょう!
テキストの紹介、引用表記、シリーズまえがきは、このリンクの記事をご参照ください。
テキストで使用するデータは、R・Stan等のサンプルスクリプトで指定されています。
サンプルスクリプトは著者GitHubサイトからダウンロードして取得できます。
第5章 時系列データ同士の関係の評価
この記事は「5.7 時系列クラスタリング」「5.8 再帰定量化分析」「5.9 グレンジャー因果性検定とVARモデル」を実践いたします。
インポート
この章で用いるライブラリをインポートします。
### インポート
# 基本
import numpy as np
import pandas as pd
# Rデータセット読み取り
import statsmodels.api as sm
import rdata
# WEBアクセス/googleトレンド
import requests
from pytrends.request import TrendReq
# Zipファイル操作
import zipfile
# データ前処理
from sklearn.preprocessing import StandardScaler
# 日付処理
from datetime import datetime
from dateutil import tz
# DTW処理
# pip install dtw_python
from dtw import dtw
# 信号処理
from scipy.signal import coherence, periodogram
import scipy.signal as signal
# 方向データの統計処理
# pip install pingouin
import pingouin as pg
# 階層的クラスタリング、デンドロビウム描画
from sklearn.cluster import AgglomerativeClustering
from scipy.cluster.hierarchy import dendrogram
# VAR・AR
from statsmodels.tsa.vector_ar.var_model import VAR
from statsmodels.tsa.ar_model import AutoReg
# グラフ描画
import matplotlib.pyplot as plt
import seaborn as sns
plt.rcParams['font.family'] = 'Meiryo'
# ワーニング表示の抑制
import warnings
warnings.simplefilter('ignore')【補足】パッケージのインストール
利用環境に応じてパッケージをインストールしてください。
以下はインストールの参考コードです。
### インストール
## dtw-python
# anaconda
conda install -c conda-forge dtw-python
# pip
pip install dtw-python
## pingouin
# anaconda
conda install -c conda-forge pingouin
# pip
pip install pingouin
時系列クラスタリング
類似する複数の時系列データをクラスタに分けます。
時系列データ間の距離の算出には dtw_python パッケージの dtw を利用します。
① データの作成
100期のランダムウォークを30個作成します。
乱数の生成結果がテキストと異なるため、クラスタリング結果等もテキストと異なる内容になります。
### データの作成
# ランダムウォークを返す関数の定義
def random_walk_1D(n):
return np.cumsum(np.random.randn(n))
# 初期値設定
N = 30 # 時系列サンプルの数
LEN = 100 # 時系列サンプルのサイズ:1標本当たり100time
np.random.seed(1)
# 時系列データの作成 100期(行)のランダムウォークデータを30標本(列)作成
data = pd.DataFrame([random_walk_1D(LEN) for i in range(N)]).T
# 時系列データの表示
print('data.shape:', data.shape)
display(data.head())
【実行結果】

② クラスタリング前のデータを描画
ひとまず描画します。
### 描画
plt.plot(data, lw=0.4, color='tab:gray')
plt.xlabel('data');【実行結果】
(予告)モノトーンの線がクラスタリングによって色鮮やかになります!

③ DTW距離の算出とデンドログラムの描画
時系列データ間のDTW距離を計算して、デンドログラムを描画します。
まずはデンドログラム描画関数です。
scikit-learn 公式サイトで公開されている描画関数をお借りします!
### デンドログラム作成関数 次のサイトよりコードを引用
def plot_dendrogram(model, **kwargs):
counts = np.zeros(model.children_.shape[0])
n_samples = len(model.labels_)
for i, merge in enumerate(model.children_):
current_count = 0
for child_idx in merge:
if child_idx < n_samples:
current_count += 1 # leaf node
else:
current_count += counts[child_idx - n_samples]
counts[i] = current_count
linkage_matrix = np.column_stack([model.children_, model.distances_,
counts]).astype(float)
dendrogram(linkage_matrix, **kwargs)【実行結果】なし
続いて、DTW距離の算出とデンドログラムの描画を実行します。
テキストの図5.18上に相当します。
dtw でDTW距離を計算して、scikit-learn の AgglomerativeClustering で4つのクラスタにクラスタリングします。
### DTW距離の算出とデンドログラムの描画 図5.18上に相当
## DTW距離の距離行列の作成
# 距離行列の初期化
distance_matrix = np.zeros((len(data.columns), len(data.columns)))
# 30系列の時系列データのペアごとにDTW距離を算出して距離行列に格納
for i in range(len(data.columns)):
for j in range(len(data.columns)):
# dtwライブラリでDTW距離を算出
align = dtw(data.iloc[:, i].values, data.iloc[:, j].values,
keep_internals=True)
# DTW距離を距離行列に格納
distance_matrix[i, j]= align.distance
## デンドログラムの描画
# ward法を用いた凝集的クラスタリングで距離行列のクラスタリングを実施
model = AgglomerativeClustering(n_clusters=4, # クラスタ数:4
linkage='ward', # ward法
compute_distances=True) # 距離計算する
model = model.fit(distance_matrix)
# デンドログラムの描画
plot_dendrogram(model)
plt.title('Hierarchical Clustering Dendrogram')
plt.show()【実行結果】
30個の時系列データがDTW距離の近いもの同士くっついています。

④ 時系列クラスタリング結果の描画
上記③のクラスタリング結果は「model」に格納されています。
この model からクラスタリングラベル label を取り出して色分けします。
テキストの図5.18下に相当します。
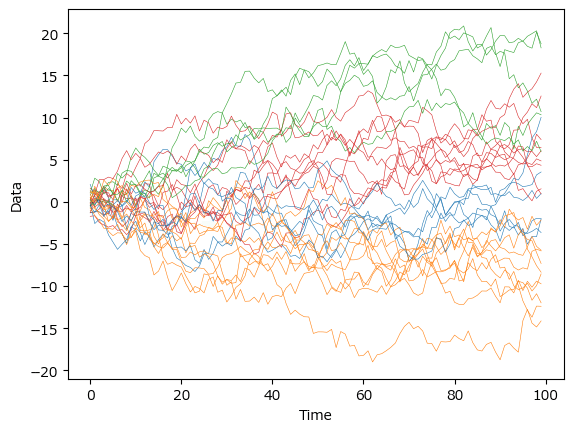
### 30の時系列データを4つのクラスタごとに色を変えて描画 ※図5.18下に相当
# 色の設定
colors = ['tab:orange', 'tab:red', 'tab:green', 'tab:blue']
# 描画
for i in range(len(data.columns)):
# model.labels_で所属クラスタ番号を取得
plt.plot(data.iloc[:, i], color=colors[model.labels_[i]], lw=0.4)
# 修飾
plt.xlabel('Time')
plt.ylabel('Data')
plt.show()【実行結果】
近くのデータ同士が同じクラスタに分けられて、緑・赤・青・黄の4つのクラスタリングの完成です。

再帰定量化分析
■ 再帰定量化分析の概要の概要(テキストより)
テキストによると、再定量化分析(RQA)は非線形時系列解析と呼ばれる分野の代表的手法であり、時系列の局所的な時間相関を視覚化する方法、だそうです(むむむ難しい)。
複数時点のデータをまとめて多次元空間の1点として扱う「埋め込み操作」が特徴的で、「埋め込み遅延時間 $${\tau}$$の決定」「埋め込み次元 $${m}$$の決定」「リカレンスプロット描画&指標算出」が重要そうです。
■ Python の再帰定量化分析パッケージ調査
Pythonの再帰定量化分析パッケージを探してみましたが、私のリサーチ力不足もあり、埋め込み操作(遅延時間・次元)を明示的に与えられるパッケージを見つけることができませんでした(泣)
なお、リサーチの過程で「Pythonのリカレンスプロットまとめサイト」を見つけたので共有いたします。
ぜひご参考になさってくださいな。
■ リカレンスプロットの雰囲気
まずはリカレンスプロットの参考例としてよく取り上げられるコードをお借りして、リカレンスプロットのイメージを把握しておきましょう。
### リカレンスプロット描画関数 ※コードは以下のサイトより引用
# https://www.kaggle.com/code/tigurius/recuplots-and-cnns-for-time-series-classification/notebook
# modified from https://stackoverflow.com/questions/33650371/recurrence-plot-in-python
# インポート
import sklearn as sk
# プロット関数
def recurrence_plot(s, eps=None, steps=None):
if eps==None: eps=0.1
if steps==None: steps=10
d = sk.metrics.pairwise.pairwise_distances(s)
d = np.floor(d / eps)
d[d > steps] = steps
#Z = squareform(d)
return d
# 描画の実行
fig = plt.figure(figsize=(15,14))
# ランダムな時系列データの描画
random_series = np.random.random(1000)
ax = fig.add_subplot(1, 2, 1)
ax.imshow(recurrence_plot(random_series[:,None]))
# sin波な時系列データの描画
sinus_series = np.sin(np.linspace(0,24,1000))
ax = fig.add_subplot(1, 2, 2)
ax.imshow(recurrence_plot(sinus_series[:,None]));【実行結果】
左がランダムな時系列データ、右がsin波を用いた時系列データのリカレンスプロットだそうです。

この記事では、テキストの再現を断念し、いくつかの壁を乗り越えた先に広がる幾何学模様の美しさを堪能することに専念いたします。

では Python をスタートします!
① データの読み込み
Rのcrqaパッケージに含まれる「対話中の2人の手の動きの速度」に関するデータセットを読み込みます。
がしかし!
crqaパッケージ本体に含まれるデータ「crqa.RData」やデータセット単独でダウンロード可能なファイルに含まれるデータ「Rdata.rdb」からPythonで扱えるようにデータを取り出す方法が分かりません!!!
受難・・・。
苦肉の策
「GoogleコラボでRを動かして」crqaパッケージからデータセットを取り出し、csvファイルにします!
イメージ図です。

手順1:GoogleドライブをマウントしてRランタイムを起動
まず、このサイトの情報をお借りして、GoogleコラボでPythonランタイム立ち上げ→Googleドライブのマウント→Rランタイム立ち上げを行います。
ちなみにGoogleドライブマウントのコードは次のとおりです。
from google.colab import drive
drive.mount('/content/drive')手順2:Rコードを動かしてcsvをゲットする
Rランタイムに切り替えた後、次のRコードを1コードずつ実行します。
### cqraパッケージのインストール
install.packages("crqa")### cqraパッケージの呼び出し
library(crqa)### データの読み込み
data(crqa)### csvファイルの書き出し
write.csv(handmovement, file="handmovement.csv", row.names=F)手順3:csvファイルのダウンロード
下図の手順で「handmovement.csv」をダウンロードして、Python環境に配置しましょう(完)

お疲れ様でした。
ちなみに私はローカルPC上の R Studio で上記 Rコードを実行しました。

再開します。
② データの読み込みと前処理
ダウンロードしたcsvファイルをpandas のデータフレームに読み込んで、2人の動きをts1とts2に別々に格納します。
### データの読み込み
# ダウンロード済みのcsvファイルを読み込み
hand = pd.read_csv(r'./handmovement.csv')
display(hand)
# データの前処理
ts1 = hand.iloc[:300, 0]
ts2 = hand.iloc[:300, 2]
print('ts1.shape:', ts1.shape)
display(ts1)
print('ts2.shape:', ts2.shape)
display(ts2)【実行結果】
handmovementデータの内、1人目のP1_TT_d列と2人目のP2_TT_d列から前半300行(300期)のデータを取り出して、ts1、ts2を作りました。


③ ts1、ts2の描画
ts1、ts2の時系列折れ線グラフを描画します。
テキストの図5.19に相当します。
### ts1、ts2の描画 ※図5.19に相当
plt.figure(figsize=(10, 3))
plt.plot(range(300), ts1, label='ts1', lw=0.7, color='tab:blue')
plt.plot(range(300), ts2, label='ts2', lw=0.7, color='tomato')
plt.xlabel('Time')
plt.legend()
plt.show()【実行結果】
1人目は前半の0~180期くらいに動き(速度)があり、2人目は後半の140~300期くらいに動きがあります。

④ リカレンスプロットの描画
RECLACパッケージを利用してリカレンスプロットを描画してみます。
RECLACを選んだ理由は、メジャーだからということではなく、リカレンスプロット用のデータ作成や指標計算について、何となく使い勝手が良さそうに感じたからです(直感✨)。
### インストール
pip install RECLAC### インポート
import RECLAC.recurrence_plot as recでは描画します。
テキストの図5.20を目指します。
前半では RECLAC の rec.RP()を用いて2人のリカレンス行列を算出します。
算出に当たって、「埋め込み遅延時間」や「埋め込み次元」の指定を行っていません。
このあたりがテキストのRで実行した内容との相違要因になりえそうです。
後半では色合い等の設定のしやすさから matplotlib を用いて2人分のリカレンスプロットを描画します。
### リカレンスプロット(と思われるもの)の描画
## リカレンス行列の算出
# リカレンスプロットオブジェクトの生成
rp1 = rec.RP(ts1.values, method='distance', thresh=0.01)
rp2 = rec.RP(ts2.values, method='distance', thresh=0.01)
# リカレンス行列の算出
a_rm_wn1 = rp1.rm()
a_rm_wn2 = rp2.rm()
## リカレンス行列の描画
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(6, 6), sharex=True, sharey=True)
# ts1の描画
ax1.imshow(a_rm_wn1, origin='lower', cmap='OrRd')
ax1.set(xlabel='$t$', ylabel='$t$', title='ts1')
# ts2の描画
ax2.imshow(a_rm_wn2, origin='lower', cmap='OrRd')
ax2.set(xlabel='$t$', title='ts2')
plt.tight_layout();【実行結果】
赤錆色の風合いが良きです!
テキスト掲載のグラフに相当するのは左側です。
上下反転するとテキストの図5.20に近づきます。
ts1の右上(つまり200期以降)の茶色多めの領域は、テキストの記述「最後の1/3の時間帯は前半と異なる振る舞いをしていることが分かります」に相当します。

描画関数 imshow() の引数 cmap で色の指定ができます。
お好みの色彩を指定してみてはいかがでしょう。
ax1.imshow(a_rm_wn1, origin='lower', cmap='OrRd')
cmapカタログはこちらのmatplotlib公式サイトでご確認くださいね。
⑤ RQAの指標の算出
リカレンス行列を格納した rp1、rp2からRQA指標を取り出してみましょう。
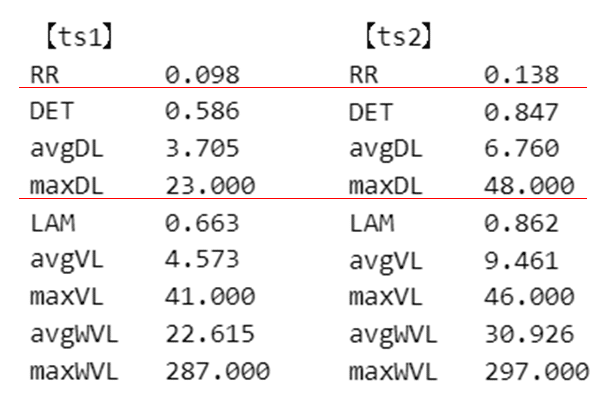
# RQA指標の算出 compute all RQA measures and print them:
# 'RR' recurrence rate ※たぶん再帰率REC
# 'DET' determinism
# 'avgDL' average diagonal line length
# 'maxDL' maximum diagonal line length ※たぶん最大線長Lmax
# 'LAM' laminarity
# 'avgWVL' average vertical line length
# 'maxWVL' maximum vertical line length
d_rqa1 = rp1.RQA(lmin=2, measures='all', border=None)
print('【ts1】')
for k, v in d_rqa1.items():
print(f'{k}\t {v:.3f}')
print('\n【ts2】')
d_rqa2 = rp2.RQA(lmin=2, measures='all', border=None)
for k, v in d_rqa2.items():
print(f'{k}\t {v:.3f}')【実行結果】
テキスト掲載の指標「再帰率」にあたるのはおそらく「RR」、「最大線長」はおそらく「maxDL」と思っています(あくまで想像)。
テキストと値が異なっていますが、原因はよく分かっていません。
相互再帰定量化分析(CRQA)にはリーチできませんでした。
現時点では断念します(泣)

グレンジャー因果性検定とVARモデル
テキストによると、グレンジャー因果性検定は、複数の時系列データ間の「因果関係」を検討するために経済学分野で開発された手法、とのこと。
ベクトル自己回帰モデル(VARモデル)を構築して、グレンジャー因果性検定を行い、インパルス応答関数でデータ間の詳細な影響関係を調べます。
■ 参考書籍
実務的なPython時系列分析の決定版ともいえる書籍のご紹介です。
グレンジャー因果性・インパルス応答関数についても、理論を平易に紐解き、Pythonサンプルコードを動かして、サクッと理解を促進してくれます。
また「予測」に力点が置かれているので、時系列予測タスクに利用できる多くのアルゴリズムやコード例が掲載されています。
■ テキストのVARモデル
時系列データである「気分$${y_1}$$」と「活動量$${y_2}$$」の関係を調べます。
1期前の状態を考慮する1次のVARモデル:VAR(1)の数式です。
$$
\begin{align*}
y_{1, t} &= c_1 + \phi_{1, 1} y_{1, t-1} + \phi_{1, 2} y_{2, t-1} + \varepsilon_{1, t} \\
y_{2, t} &= c_2 + \phi_{2, 1} y_{1, t-1} + \phi_{2, 2} y_{2, t-1} + \varepsilon_{2, t} \\
\end{align*}
$$
$${\phi_{1, 1}}$$は1時点前の気分$${y_{1, t-1}}$$が現在の気分に及ぼす影響の強さを示す偏回帰係数
$${\phi_{1, 2}}$$は1時点前の気分$${y_{2, t-1}}$$が現在の気分に及ぼす影響の強さを示す偏回帰係数
VAR(1)モデルに傾きや係数を設定して日本語にすると次のようになります。
$$
\begin{align*}
気分y_1&=10+0.3 \times 1時点前の気分+0.6\times 1時点前の活動量 + \varepsilon_{1t}\\
活動量y_2&=20-0.5 \times 1時点前の気分+0.5\times 1時点前の活動量 + \varepsilon_{2t} \\
\end{align*}
$$
① データの作成
テキストのRコードをお借りして、上記の日本語数式の内容でデータを作成します。
乱数生成がテキストと異なるため、出来上がったデータや分析内容はテキストと異なります。予めご了承くださいませ。
### 仮想時系列データの生成
## 初期値設定
N = 100 # データ数
np.random.seed(456) # 乱数シード
## 撹乱項ε:epの生成 ※多変量正規分布の乱数 shape=(100, 2)
mu = np.array([0, 0]) # 平均ベクトル
cov = np.array([[1, 0.8], [0.8, 1]]) # 分散共分散行列
ep = np.random.multivariate_normal(mean=mu, cov=cov, size=N) # 撹乱項(乱数)
## y1:気分、y2:活動量の生成
# y1,y2の初期化
y1, y2 = np.zeros(N), np.zeros(N)
# y1,y2のt=0の算出
y1[0] = 25 + ep[0, 0]
y2[0] = 10 + ep[0, 1]
# y1,y2のt=1以降の算出
for i in range(1, N):
y1[i] = 10 + 0.3 * y1[i-1] + 0.6 * y2[i-1] + ep[i, 0]
y2[i] = 20 - 0.5 * y1[i-1] + 0.5 * y2[i-1] + ep[i, 1]
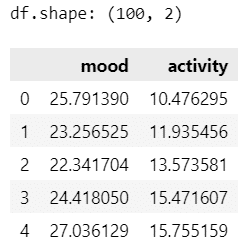
## データフレーム化
df = pd.DataFrame({'mood': y1, 'activity': y2})
print('df.shape:', df.shape)
display(df.head())【実行結果】
100期に渡る mood:気分、activity:活動量のデータです。
② データの描画
VAR(1)モデルの2つの時系列データの折れ線グラフを描画します。
テキストの図5.23に相当します。
### 時系列データの描画 ※図5.23に相当
fig, ax = plt.subplots(figsize=(8, 4))
df.plot.line(ax=ax, color={'mood': 'cornflowerblue', 'activity': 'tomato'})
ax.set(ylim=(-2, 42), yticks=([0, 10, 20, 30, 40]), xlabel='Time');【実行結果】


③ VARモデルの選択
statsmodelsのVAR()を用いて、気分・活動量データの最適な次数を探ります。
セールスアナリティクスさんのコードを参考にさせていただきました。
ありがとうございます!
### VAR(p)モデルの選択
# コード参考
# https://www.salesanalytics.co.jp/datascience/datascience128/
# 公式サイト
# https://www.statsmodels.org/dev/generated/statsmodels.tsa.vector_ar.var_model.VAR.html
# モデルのインスタンス生成
model_var = VAR(df)
# 最適な次数の探索(AICで選択) trend='c':定数項を含める
lag_order = model_var.select_order(maxlags=5, trend='c')
# 最適な次数の探索結果を格納
lag = lag_order.selected_orders
# 結果表示
print(f" 最適な次数: {lag['aic']}, (AIC)\n")
print('【各情報規準の最適な次数】')
display(pd.Series(lag, name='最適なラグ').to_frame().T)
print('【次数と情報量規準の計算値】')
display(pd.DataFrame(lag_order.ics).T)【実行結果】
4つの情報規準のすべてが「次数1が最適」と申しております!
VAR(1)です。

④ VARモデルの係数の推定
VAR()のインスタンス model_var に対して fit を実行することで、VAR(1)モデルの切片・傾きを推定できます。
### モデルの学習
result_var = model_var.fit(maxlags=lag['aic'], trend='c') # 'c':定数項を含める
print(result_var.summary())【実行結果(一部抜粋)】
気分$${y_1}$$の切片・傾きは「Results for equation mood」、活動量$${y_2}$$の切片・傾きは「Results for equation activity」の「coefficient」に掲載されています。
「const」が切片、「L1.mood」が気分の傾き、「L1.activity」が活動量の傾きです。
「prob」を見るとすべての切片・傾きは値が$${0.002}$$以下です。
有意水準$${5\%}$$で切片・傾きは有意ということになります。

⑤ AR(1)モデルとVAR(1)モデルの比較
2つのモデルの予測値を比較します。
ARモデルは statsmodels の AutoReg() を用います。
### ARモデルによる予測と観測値・ARモデル・VARモデルのデータ比較
# ARモデルの学習
result_ar = AutoReg(df['mood'], lags=1, trend='c').fit()
# データフレーム化
df2 = pd.DataFrame({'mood': df['mood'][1:], # 観測値
'AR': result_ar.fittedvalues, # ARモデルの予測
'VAR': result_var.fittedvalues.iloc[:, 0]}) # VARモデルの予測
display(df2)【実行結果】
観測値と予測値を見てもAR(1)モデルとVAR(1)モデルの違いはよく分かりません。

観測値と2つのモデルの予測値を可視化します。
pandas の plot.line を利用します。
テキストの図5.24に相当します。
### y1:moodの予測値の描画 ※図5.24に相当
fig, ax = plt.subplots(figsize=(8, 4))
df2.plot.line(ax=ax, lw=0.9, xlabel='Time', ylabel='value',
color={'mood': 'dimgray', 'AR': 'deeppink', 'VAR': 'mediumblue'})
ax.set(ylim=(21, 31), yticks=([22, 24, 26, 28, 30]))
ax.legend(['mood', 'AR(1)', 'VAR(1)']);【実行結果】
グレーが気分の観測値、赤がAR(1)、青がVAR(1)です。
正直なところ、どちらのモデルの予測値のほうが精度が高いのか、分かりかねます。。。(違いの出やすいデータを作ればよかったかな。。。)

RMSEを見てみましょう。
### RMSEの比較
from sklearn.metrics import mean_squared_error as MSE
print(f"RMSE AR(1) : {MSE(df2['mood'], df2['AR'], squared=False):.3f}")
print(f"RMSE VAR(1): {MSE(df2['mood'], df2['VAR'], squared=False):.3f}")【実行結果】
RMSEの値の小さなVAR(1)モデルのほうが精度が高い、という結果になりました(よかったです)。
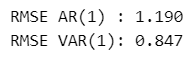

⑥ グレンジャー因果性検定
活動量$${y_2}$$から気分$${y_1}$$への因果性と、気分$${y_1}$$から活動量$${y_2}$$への因果性についてグレンジャー因果性検定を実施します。
帰無仮説は「(から側の変数の)回帰係数は0である」(因果性がない)です。
VARモデルを fit させた result_var に対して test_causality を実行します。
引数上、気分$${y_1}$$が0、活動量$${y_2}$$が1です。
原因側をcausing で、結果側をcaused で指定します。
まずは、活動量$${y_2}$$から気分$${y_1}$$への因果性。
### VAR(1)モデルのグレンジャー因果性検定1 y2.acrivity:0からy1.mood:0への因果性
gran_test_result1 = result_var.test_causality(causing=1, caused=0)
print(gran_test_result1.summary())【実行結果】
p値は0.000。有意水準$${5\%}$$で帰無仮説は棄却でき、因果性あり、ということになります。

続いて、気分$${y_1}$$から活動量$${y_2}$$への因果性。
### VAR(1)モデルのグレンジャー因果性検定2 y1.mood:0からy2.acrivity:0への因果性
gran_test_result2 = result_var.test_causality(causing=0, caused=1)
print(gran_test_result2.summary())【実行結果】
p値は0.000。有意水準$${5\%}$$で帰無仮説は棄却でき、因果性あり、ということになります。

テキストでは、グレンジャー因果性検定を行う際に、各変数が定常性を満たす必要があるとのこと。
ADF検定を実行しましょう。
statsmodels の adfuller を利用します。
### ADF検定 帰無仮説「単位根がある」
from statsmodels.tsa.stattools import adfuller
for col in df.columns:
res = adfuller(df[col], regression='c')
print(f'{col}:')
print(f' ADF stats:{res[0]:.3f}, p value:{res[1]:.3f}, use lag:{res[2]}')【実行結果】
気分:mood は p値 が 0.07。有意水準$${5\%}$$の場合、帰無仮説を棄却できず、単位根あり(定常性なし)です、がっかり。


⑦ 非直交化インパルス応答関数
VARモデルに関する「非直交化インパルス応答関数」を確認します。
テキストによると、気分$${y_{1,t}}$$の誤差項$${\varepsilon_1}$$に1単位のショックを与えたとき、$${k}$$時点後に生じる活動量$${y_{2,t+k}}$$の変化のことを、$${y_1}$$のショックに対する$${y_2}$$の非直交化インパルス応答、$${k}$$の関数は非直交化インパルス応答関数、とそれぞれ呼ぶそうです。
非直交化インパルス応答関数の描画をしてみましょう。
VARモデルを fit させた result_var に対して irf() を実行します。
描画関数の引数 orth=False とすることで、「非直交化」となります。
テキストに図5.26に相当します。
### (非直交化)インパルス応答関数
# 左の変数の誤差項にショックを与える→右の変数に影響
# VARモデルの学習結果からirf:Impulse Response functionを取得
impulse_func = result_var.irf(periods=5)
# 非直交化インパルス応答関数の描画 ※orth=False:非直交化
impulse_func.plot(orth=False, figsize=(6, 6), seed=123)
# 修飾
plt.tight_layout()
plt.show()【実行結果】
気分:moodから活動量:activityへは、下がってから上がる傾向です。
活動量:activityから気分:moodへは、上がってから下がる傾向です。

⑧ 直交化インパルス応答関数
気分と活動量の誤差項同士の相関を考慮したものが「直交化インパルス応答関数」です。
直交化インパルス応答関数の描画をしてみましょう。
VARモデルを fit させた result_var に対して irf() を実行します。
描画関数の引数 orth=True とすることで、「直交化」となります。
テキストに図5.27に相当します。
### 直交化インパルス応答関数
# 左の変数の誤差項にショックを与える→右の変数に影響
# VARモデルの学習結果からirf:Impulse Response functionを取得
impulse_func = result_var.irf(periods=5)
# 非直交化インパルス応答関数の描画 ※orth=True:直交化
impulse_func.plot(orth=True, figsize=(6, 6), seed=123)
# 修飾
plt.tight_layout()
plt.show()【実行結果】
気分:mood から活動量:acticity のインパルス応答関数は、非直交化と比べて形状が大きく変わりました。

以上で終了です。
お疲れ様でした。

第6章 へ続く
■次回の取り組みテーマ
多変量時系列データの要約に関連する次のトピック
・次元削減の際の注意点(ラグ・位相差)
・非負値行列因子分解
・動的因子分析
次の記事
前の記事
目次
ブログの紹介
note で4つのシリーズ記事を書いています。
ぜひ覗いていってくださいね!
1.のんびり統計
統計検定2級の問題集を手がかりにして、確率・統計をざっくり掘り下げるブログです。
雑談感覚で大丈夫です。ぜひ覗いていってくださいね。
統計検定2級公式問題集CBT対応版に対応しています。
2.実験!たのしいベイズモデリングをPyMC Ver.5で
書籍「たのしいベイズモデリング」の心理学研究に用いられたベイズモデルを PyMC Ver.5で描いて分析します。
この書籍をはじめ、多くのベイズモデルは R言語+Stanで書かれています。
PyMCの可能性を探り出し、手軽にベイズモデリングを実践できるように努めます。
身近なテーマ、イメージしやすいテーマですので、ぜひぜひPyMCで動かして、一緒に楽しみましょう!
3.Python機械学習プログラミング実践記
書籍「Python機械学習プログラミング PyTorch & scikit-learn編」を学んだときのさまざまな思いを記事にしました。
この書籍は、scikit-learn と PyTorch の教科書です。
よかったらぜひ、お試しくださいませ。
4.データサイエンスっぽいことを綴る
統計、データ分析、AI、機械学習、Python のコラムを不定期に綴っています。
「統計」「Python」「数学とPython」「R」のシリーズが生まれています。
最後までお読みいただきまして、ありがとうございました。
