
時系列分析入門【第6章 前編】非負値行列因子分解・動的因子分析をPythonで実践する
この記事は、テキスト「RとStanではじめる 心理学のための時系列分析入門」の第6章「多変量時系列データの要約」のRスクリプトをお借りして、Python で「実験的」に実装する様子を描いた統計ドキュメンタリーです。
取り扱いテーマは多変量時系列データの要約に関連する以下のトピックです。
・非負値行列因子分解
・動的因子分析
かなり難易度の高いトピックなので、今回はもっともっと波乱万丈!
(注)波乱だらけということ
さあ、時系列分析を楽しんでいきましょう!
テキストの紹介、引用表記、シリーズまえがきは、このリンクの記事をご参照ください。
テキストで使用するデータは、R・Stan等のサンプルスクリプトで指定されています。
サンプルスクリプトは著者GitHubサイトからダウンロードして取得できます。
第6章 多変量時系列データの要約
この記事は「6.1 次元削減」「6.2 非負値行列因子分解」「6.3 動的因子分析」を実践いたします。
インポート
この章で用いるライブラリをインポートします。
### インポート
# 基本
import numpy as np
import pandas as pd
# WEBアクセス
import requests
# Rデータ読み取り
import rdata
# Rデータセット・動的因子分析
import statsmodels.api as sm
# 非負値行列因子分解
from sklearn.decomposition import NMF
# グラフ描画
import matplotlib.pyplot as plt
import seaborn as sns
plt.rcParams['font.family'] = 'Meiryo'
# ワーニング表示の抑制
import warnings
warnings.simplefilter('ignore')
時系列データの次元削減とは
多次元データのもつ意味を保ちつつ、少ない次元にデータを圧縮することです。
テキストでは、時系列分析で用いられる次元削減の目的について、次の2点を挙げています。
1.時点×変数 → 今回のコード化対象
1つの対象(1人の対象者など)の多数の変数を測定してできる「時点×多数の変数」データの変数を要約することで、時間のダイナミクスを少数の成分・因子で説明する。
動的因子モデル(DFA)などが用いられる。
2.時点×対象 → 次回のコード化対象
1つの変数について複数の対象(複数の対象者など)のデータを測定してできる「多数の対象(人)×時点」データの時間的なパターンを要約することで、少数の時間的パターンで個々の対象(人)の変化を説明する。
関数主成分分析(FPCA)などが用いられる。
また、時系列データの次元削減の際の注意点として、時系列データ同士の時間的なずれ(ラグ)・位相差がある場合に、ラグを分析に取り入れるか、タイミングを揃えるかの考慮が必要とのことです。
時系列データ同士の時間的なずれの図を描画します。
テキストの図6.1に相当します。
① データの読み込み
Rのfdaパッケージに含まれるデータセット「pinchraw」を読み込みます。
20人分の摘む力データです。
いったんローカルPCにダウンロードして、pandasのデータフレームに読み込みます。
### rdaファイルのダウンロード
# 設定:ダウンロードファイルの格納先パス+ファイル名
filename = r'./pinchraw.rda'
# ダウンロードの実行
url = r'https://www.psych.mcgill.ca/misc/fda/downloads/FDAfuns/R/data/' \
'pinchraw.rda'
res = requests.get(url)
with open(filename, mode='wb') as f:
f.write(res.content)【実行結果】なし
続いてpandasのデータフレームに読み込みます。
## pinchraw Rdataの読み込み https://pypi.org/project/rdata/
# ファイルの読み込み・解析
parsed = rdata.parser.parse_file(filename)
# データの変換:辞書型(中のデータ形式はxarray)
converted = rdata.conversion.convert(parsed)
# データフレーム化
pinchraw_df = pd.DataFrame(converted['pinchraw'])
display(pinchraw_df)【実行結果】
151期の時系列データが20個(20列)格納されています。

② データの描画
データを pandas の plot で描画します。
テキストの図6.1に相当します。
### 描画 ※図6.1に相当
pinchraw_df.plot(lw=0.6, ls='--', legend=False, figsize=(8, 4),
xlabel='Time(ms)', ylabel='Force(N)', xticks=range(0, 151, 50));【実行結果】
「時系列データ同士の時間的なずれの図」です。
少しずつ時間差=ラグがある様子が分かりました。


非負値行列因子分解:NMF
テキストによると、非負値行列因子分解(NMF)は動画から表情の因子を見つけ出すために使われているそうです。
そしてテキストは、FACSという表情記述方法で記述された、ある首相の辞任記者会見の表情データを用いて、NMFします。
テキストに追随しますよっ!
① データの読み込み
著者のgithubサイトよりcsvファイルを読み込みます。
### データの読み込み
# データの読み込み
url = r'https://raw.githubusercontent.com/komorimasashi/time_series_book/' \
r'90f315f0ad38f18167f6de4366e0667dda3106ed/data/abe_facial_mov.csv'
face_mov_orgn = pd.read_csv(url)
# データの前処理
face_mov_df = face_mov_orgn['frame']
face_mov_df = pd.concat([face_mov_orgn['frame'], face_mov_orgn.iloc[:, 679:696]],
axis=1)
face_mov_df.columns = ['frame'] + [x[:4] for x in face_mov_orgn.columns[679:696]]
# データフレームの表示
display(face_mov_df)
【実行結果】
30秒間×30フレーム/秒=900の時系列と、AU01からの表情筋を示す記号ごと列(全17次元)のマトリックスで動きの値を記述しています。

② データの描画
表情筋(17個)の時系列折れ線グラフを pandas の plot で描画します。
テキストの図6.2に相当します。
### 描画 ※図6.1に相当
face_mov_df.iloc[:, 1:].plot(lw=0.6, legend=False, figsize=(10, 5),
xlabel='Frame', ylabel='Score',
xticks=range(0, 751, 250))
plt.legend(title='AU', bbox_to_anchor=(1, 1))
plt.grid(lw=0.2);【実行結果】
AUの強度は0~5の値(非負値)だそうです。

③ NMFの実行
NMF:非負値行列因子分解、名称は厳ついですが、図で計算過程を見ると腹落ちしやすいかもです。
テキストの図6.3や、Webサイトの情報で「ふわっと」イメージしてみましょう。
次のサイトの冒頭「なにをやりたいのか」が分かりやすかったです。
ありがとうございます!
ではNMFを実行します。
scikit-learn の NMF を利用します。
NMF の 使い方の詳細は scikit-learn の公式サイト等でご確認下さい。
#### NMFの実行
# 関連サイト
# 公式: https://scikit-learn.org/stable/modules/generated/sklearn.decomposition.NMF.html
# 参考: https://qiita.com/nozma/items/d8dafe4e938c43fb7ad1
# モデルの作成
model_nmf = NMF(n_components=2, init='nndsvdar', random_state=111)
# モデルの学習:基底行列(因子得点)の算出
W = model_nmf.fit_transform(face_mov_df.iloc[:,1:])
# 係数行列(因子負荷量)の算出
H = model_nmf.components_【実行結果】なし
④ 基底行列の描画
上記のNMF実行で得た基底行列 W をヒートマップで描画します。
テキストの図6.4上に相当します。
### 基底行列の描画 ※図6.4上に相当 ★テキストと見た目が異なる
fig, ax = plt.subplots()
sns.heatmap(W, cmap='YlOrBr', ax=ax)
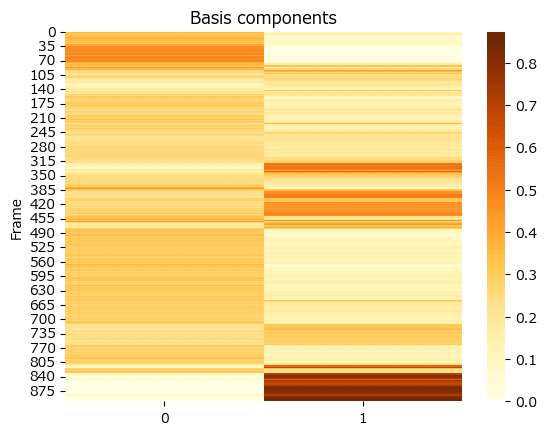
ax.set(title='Basis components', ylabel='Frame');【実行結果】
テキストの図と比べて、動きの強さ(茶色)の面積が圧倒的に小さいです。
何かやらかしたのでしょうか・・・(がっかり)。
ただ、テキストの「最初の26秒くらい(およそ780フレームまで)はあまり変化がなく、最後の数秒間で大きく表情が変化している」は、この図の右側の茶色のゾーンが示せている感じです(よかったデス)。
⑤ 係数行列の描画
上記のNMF実行で得た係数行列 H をクラスタマップで描画します。
テキストの図6.4下に相当します。
【2024/01/02更新】
seaborn の clustermap を利用してヒートマップとデンドログラム(クラスタリング)が合体した「クラスタマップ」を描画します。
ウォード法(ward)、ユークリッド距離(euclidean)を指定してクラスタリングを行っています。
### 係数行列の描画 ※図6.4下に相当 ★テキストと見た目が異なる
sns.clustermap(data=H, method='ward', metric='euclidean', row_cluster=False,
cmap='YlOrBr', cbar_pos=(1, 0.4, 0.02, 0.4),
figsize=(5, 5), xticklabels=model_nmf.feature_names_in_)
plt.text(x=-25, y=7, s='Mixture coefficients');【実行結果】
こちらもテキストと比べて、強い動き(茶色)の面積が圧倒的に小さいです。
AU01~AU45の動きの強弱の相関を確認したいのですが、あまり情報を得られそうにありません(がっかり)。
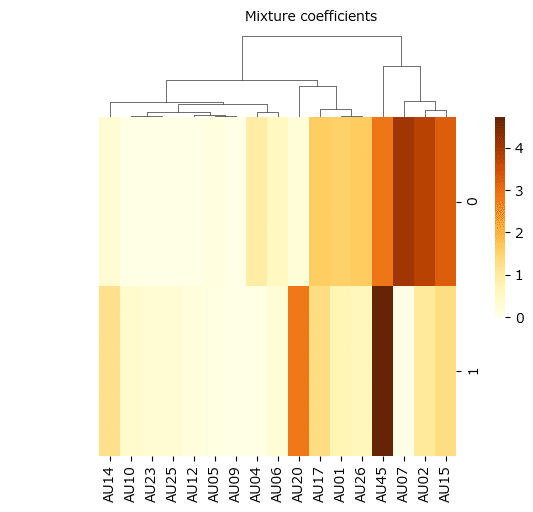
因子0では、AU02とAU07が強い値で関連してそうですが、テキストではAU04(眉下げ)とAU07(瞼の緊張)が強く関連しているとのこと。
因子1では、AU20とAU45が強い感じですが、テキストではAU10(上唇挙げ)とAU12(口角を上げる)が関連しているとのこと。
③のNMFの実行時に、うまく基底行列と係数行列を算出できなかったのでしょうか。スミマセン。

次の話題に移ります。
動的因子分析:DFA
テキストでは「状態空間モデル」と見ることができるとして、次のモデルを用いています。
$$
\begin{align*}
\boldsymbol{y}_t &= \boldsymbol{\mu} + \boldsymbol{\Lambda \text{f}}_t + \varepsilon_t ただし\varepsilon_t \sim \text{MVNormal}(\boldsymbol{0}, \boldsymbol{R}) \\
\boldsymbol{\text{f}}_t &= \boldsymbol{\text{f}}_t + \boldsymbol{w}_t ただし\boldsymbol{w}_t \sim \text{MVNormal}(\boldsymbol{0}, \boldsymbol{Q}) \\
\boldsymbol{R} &= \left[ \begin{matrix} r_1 & 0 & 0 & 0 & 0\\ 0 & r_2 & 0 & 0 & 0\\ 0 & 0 & r_3 & 0 & 0\\ 0 & 0 & 0 & r_4 & 0\\ 0 & 0 & 0 & 0 & r_5 \end{matrix}\right] \\
\boldsymbol{Q} &= \left[ \begin{matrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{matrix} \right]
\end{align*}
$$
$${\boldsymbol{R}}$$:観測値にそれぞれ独立なホワイトノイズが乗っているという設定
$${\boldsymbol{Q}}$$:因子得点$${\boldsymbol{\text{f}}_t}$$の要素がそれぞれ独立にランダムウォークすること=$${\boldsymbol{Q}}$$は単位行列$${\boldsymbol{I}_m}$$であるという設定
このあたりの情報を手がかりにして Python コードを考えました。
ただ、先に申し上げます。
Python 勝手コードはテキストと異なる結果になりました。
ここからの読み方ですが、ぜひ statsmodels に状態空間モデルの動的因子モデルが存在する、ということを覚えていってくださいね。
① データの読み込み
RのMARSSパッケージに含まれるワシントン湖のプランクトンデータ「lakeWAplanktonTrans」を利用します。
### rdaファイルのダウンロード
# 設定:ダウンロードファイルの格納先パス+ファイル名
filename = r'./lakeWAplankton.rda'
# ダウンロードの実行
url = r'https://github.com/cran/MARSS/blob/master/data/' \
'lakeWAplankton.rda?raw=true'
res = requests.get(url)
with open(filename, mode='wb') as f:
f.write(res.content)【実行結果】なし
### lakeWAplankton Rdataの読み込み https://pypi.org/project/rdata/
# ファイルの読み込み・解析
parsed = rdata.parser.parse_file(filename)
# データの変換:辞書型(中のデータ形式はxarray)
converted = rdata.conversion.convert(parsed)
# 列名の取得
cols = converted['lakeWAplanktonTrans'].coords.variables['dim_1'].data
# データフレーム化
plank_df_orgn = pd.DataFrame(converted['lakeWAplanktonTrans'].data,
columns=cols)
display(plank_df_orgn)【実行結果】

② データの前処理
1980~1990年のプランクトン量のデータを抽出します。
### データの前処理
### 1980年から1990年までのプランクトンの量のデータを抜き出す
## 設定
# 抽出条件
query = (plank_df_orgn['Year']>=1980) & (plank_df_orgn['Year']<=1990)
# 使用する列
select_cols = ['Cryptomonas', 'Diatoms', 'Cyclops', 'Unicells', 'Epischura']
# 年月インデックス
time_idx = pd.period_range(start='1980-01', end='1990-12', freq='M')
## plank_dfの作成
# 抽出条件に合致するデータから使用する列を抽出してplank_dfを作成
plank_df = plank_df_orgn[query][select_cols]
# 年月インデックスを設定
plank_df = plank_df.set_index(time_idx, drop=True)
# # データフレームの完成(行列の転置)
# plank_df = plank_df.T
## データフレームの表示
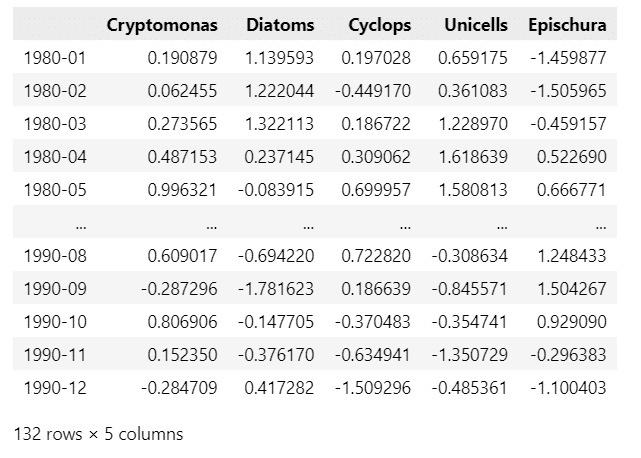
display(plank_df)【実行結果】
132か月、5種類のプランクトンの量のデータです。
③ DFAのモデル定義
statsmodels の DynamicFactor を利用して、DFAを実行します。
まずはモデルの定義から。
因子数3、因子のラグ1(ランダムウォークの条件)、ホワイトノイズの設定を検討しました。
なお、因子のAR係数に定常性を適用するTrue設定にしましたが何となく腑に落ちていません。しかしFalseにすると分析結果が欠損値だらけになってしまい・・・。
なお、statsmodels のモデルは観測方程式に平均ベクトルを含んでおらず、この点がテキストと大きく相違しています。
したがって、分析結果もテキストと大きく相違することになるでしょう(確信的予言)。
### DFAモデルの定義 statsmodelsの状態空間モデルライブラリ
# https://www.statsmodels.org/stable/generated/statsmodels.tsa.statespace.dynamic_factor.DynamicFactor.html
model_dfa = sm.tsa.DynamicFactor(
endog=plank_df, # 観測変数
k_factors=3, # 因子数
factor_order=1, # 因子の次数(ラグ)
enforce_stationarity=True, # AR係数に定常性を適用する
# 観測誤差項の設定:ホワイトノイズ
error_var=False, # VARモデルではない
error_order=0, # ARの次数は0=ホワイトノイズ
error_cov_type='diagonal', # 相関関係なし
)
# print(model_dfa.summary())【実行結果】なし
④ DFAの実行
fit メソッドでDFAを実行します。
### DFAの実行
# https://www.statsmodels.org/stable/generated/statsmodels.tsa.statespace.dynamic_factor.DynamicFactor.fit.html
result_dfa = model_dfa.fit(maxiter=10000)
print(result_dfa.summary())【実行結果】
テキストのRの出力結果とどうやって比べてよいやら、皆目見当がつきません。。。
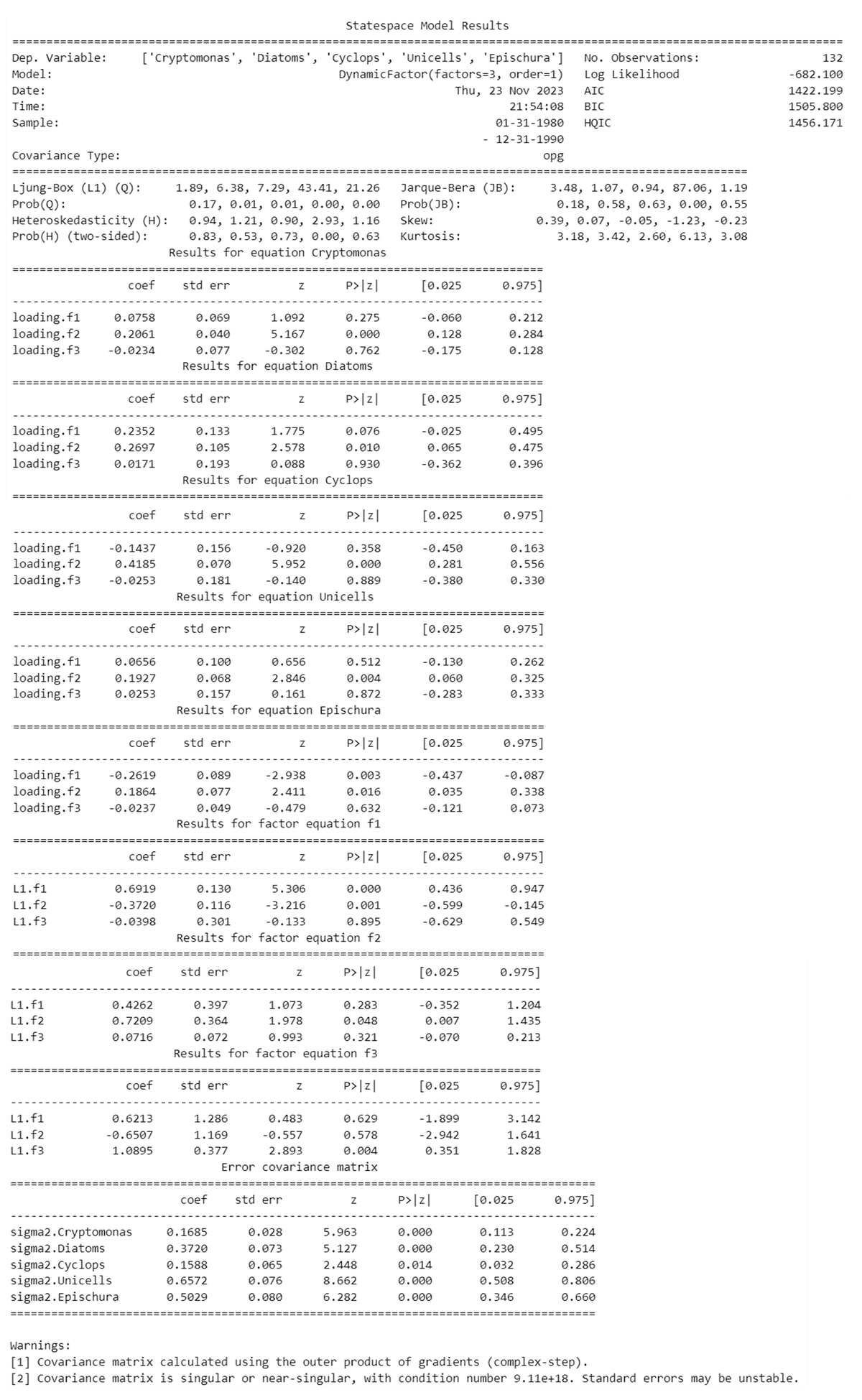
⑤ 因子得点の推定値の描画
テキストの図6.5を目指すグラフの描画です。
なお信頼区間 CI は出力しません。
### factorのプロット ※図6.5に相当
plt.figure(figsize=(10, 5))
for i in range(3):
ax = plt.subplot(2, 2, i+1)
ax.plot(result_dfa.factors['filtered'][i])
ax.set(title=f'因子{i}', ylabel='Estimate')
plt.suptitle('因子得点の推定値', fontsize=16)
plt.tight_layout();【実行結果】
因子0~2の3つの因子の動きはテキストと大きく異なります。

⑥ プランクトンの観測値・予測値のプロット
テキストの図6.6を目指してプロットします。
なお信頼区間 CI は出力しません。
### プランクトンの観測値と予測値のプロット ※図6.6に相当
plt.figure(figsize=(10, 7))
for i, col in enumerate(model_dfa.endog_names):
ax = plt.subplot(3, 2, i+1)
ax.plot(plank_df.loc[:, col].values, 'o', markersize=2, color='tab:red',
label='観測値')
ax.plot(result_dfa.fittedvalues[col].values, color='tab:blue',
label='予測値')
ax.set(title=f'{col}', ylabel='Estimate')
ax.legend()
plt.suptitle('各プランクトンの観測値、予測値', fontsize=16)
plt.tight_layout();【実行結果】
ざっくり(かつ贔屓目に見て)、テキストの予測平均値の推移と似ている感じがします。
しかし変動はこちらの方が緩やか・小さめ。

でもでも、新しい時系列データの分析方法を知ることができて幸せです🍀
今後、時系列データの分析や予測をする際、動的因子分析も選択肢に入れたいと思いました。
⑦ 診断プロット
plot_diagnostics でプランクトンごとの診断プロットを描画してみます。
### 診断プロット
for i, col in enumerate(model_dfa.endog_names):
result_dfa.plot_diagnostics(col, figsize=(10, 5))
plt.tight_layout()
plt.show()【実行結果】
残差について、残差プロット、ヒストグラム、正規Q-Qプロット、コレログラム(自己相関関数)を簡単に描画できるのは嬉しいですね!
4番目のUnicellsの正規Q-Qプロットとコレログラムにやや難がありそうです。





以上で終了です。
お疲れ様でした。

第6章 後編 へ続く
■次回の取り組みテーマ
多変量時系列データの要約に関連する「関数主成分分析(FPCA)」
(次回が最終回です)
次の記事
前の記事
目次
ブログの紹介
note で4つのシリーズ記事を書いています。
ぜひ覗いていってくださいね!
1.のんびり統計
統計検定2級の問題集を手がかりにして、確率・統計をざっくり掘り下げるブログです。
雑談感覚で大丈夫です。ぜひ覗いていってくださいね。
統計検定2級公式問題集CBT対応版に対応しています。
2.実験!たのしいベイズモデリングをPyMC Ver.5で
書籍「たのしいベイズモデリング」の心理学研究に用いられたベイズモデルを PyMC Ver.5で描いて分析します。
この書籍をはじめ、多くのベイズモデルは R言語+Stanで書かれています。
PyMCの可能性を探り出し、手軽にベイズモデリングを実践できるように努めます。
身近なテーマ、イメージしやすいテーマですので、ぜひぜひPyMCで動かして、一緒に楽しみましょう!
3.Python機械学習プログラミング実践記
書籍「Python機械学習プログラミング PyTorch & scikit-learn編」を学んだときのさまざまな思いを記事にしました。
この書籍は、scikit-learn と PyTorch の教科書です。
よかったらぜひ、お試しくださいませ。
4.データサイエンスっぽいことを綴る
統計、データ分析、AI、機械学習、Python のコラムを不定期に綴っています。
「統計」「Python」「数学とPython」「R」のシリーズが生まれています。
最後までお読みいただきまして、ありがとうございました。
