
ScratchでARプログラミング入門 ⑦再帰処理でフラクタル図形に挑戦!
前回の復習
前回は、「文字を書く」ブロックを使って、AR空間に文字を描画する方法を学びました。
ボクセルで文字を表現することで、3D案内表示やマトリックスの世界を簡単に再現できましたね。
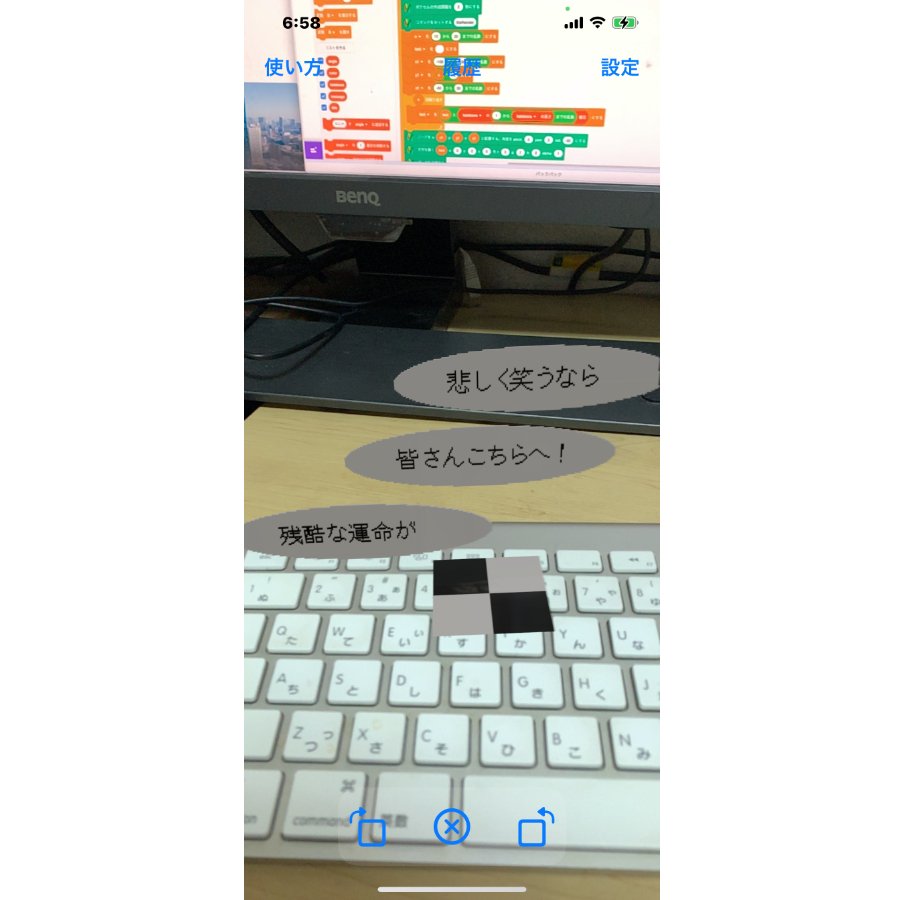
前回の問題の回答例を発表します。上記の図1の3Dメッセンジャーを描くスクリプトは、次のようになります。


繰り返しブロックを使って、messageリストのメッセージを空間にランダムな位置に描きます。messageリストには、好きな言葉を入れてください。ボクセラミングを実行しているデバイスの性能にもよりますが、メッセージの数は2~5個程度保存できます。
ボクセルの作成間隔を0にすると、瞬時にメッセージを表示します。
liteRender コマンドでボクセルの描画を簡略化すると、描画負荷を軽減できます。これにより、多くのボクセルを配置できます。
楕円形の数式 $${x^2 + (4 y)^2 = r^2}$$ を条件式に使って、楕円形の内側に白いボクセルを配置します。この楕円形が、メッセージの背景枠になります。
「文字を書く」ブロックで、メッセージを描きます。メッセージサイズに合わせて、表示位置をx, y, zで指定します。z = 1にすることで、背景枠の手前に表示できます。
読み始める前に
この記事では、私たちが開発した無料ARプログラミング学習アプリ「ボクセラミング(Voxelamming)」の使い方を、Scratchのサンプルコードと共に詳しく解説していきます。
iPhone/iPad/Vision Proをお持ちの方は、App StoreからVoxelammingアプリをダウンロードして、ぜひ一緒にプログラミングに挑戦してみましょう!
フラクタル図形に挑戦!
今回は、フラクタル図形と呼ばれる、不思議な図形を描画する方法を学びます。
フラクタル図形とは、一部分を拡大すると、全体と同じような形が現れる図形のことです。
自然界にも、雪の結晶や木の枝分かれ、海岸線など、フラクタル図形とよく似た形が、数多く存在します。
これらの形には、「フラクタル」と呼ばれる、不思議な法則が隠されていることがあります。
フラクタルとは、一部分が全体と自己相似になっている図形のことです。次の図は、Pythonのタートルグラフィックスで描いたフラクタル図形の例です。シェルピンスキーの三角形と呼ばれる図形です。

ボクセラミングでも、再帰処理と呼ばれるプログラミングのテクニックを使うことで、美しいフラクタル図形を表現することができます。
しかし、再帰関数とフラクタル図形は、少し難しい概念です。
頭を柔らかくして、じっくりと考えていく必要があるので、気合を入れて読み進めていきましょう!
再帰処理:自分自身を呼び出す魔法
フラクタル図形を描くには、再帰処理というプログラミングテクニックを用います。
再帰処理とは、プログラムの中で、自分自身を呼び出す処理のことです。
「自分自身を呼び出すって、どういうことだろう?」
と思うかもしれませんね。
例えば、鏡の中に鏡が映っている様子を想像してみてください。
鏡の中に映った鏡の中に、さらに鏡が映り…と、無限に鏡が続いていくように見えますよね?
再帰処理も、これと似たようなイメージです。
関数が自分自身を呼び出すことで、同じ処理が繰り返され、複雑なパターンが生まれます。
座標軸を積み重ねる「マトリックス」
ボクセラミングでは、マトリックスと呼ばれる機能を使って、座標軸を積み重ねることができます。
「座標軸を積み重ねる」とは、どういうことでしょうか。
少し難しい言葉ですが、イメージとしては、積み木を積み重ねていくような感じです。
push_matrix ブロックで現在の座標軸を保存し、translate ブロックや rotate ブロックで座標軸を移動したり回転させたりした後に、pop_matrix ブロックで保存した座標軸を復元することができます。
このマトリックス機能を使うことで、フラクタル図形のように、複雑な構造を持つオブジェクトを、簡単に描画することができます。
3Dフラクタルツリーを作ろう!
再帰処理とマトリックス機能を使って、AR空間に3Dのフラクタルツリーを作ってみましょう。
挑戦してみよう!
一本の線分から開始します。
線分の先端から、3つの枝を分岐させます。
分岐した枝の先端から、さらに3つの枝を分岐させます。
この処理を繰り返すことで、木のような形を作ることができます。
ヒント
再帰関数を定義し、その中で自分自身を呼び出すようにします。
再帰レベルを設定し、再帰の深さを制御します。
push_matrix ブロックと pop_matrix ブロックを使って、座標軸を管理します。
translate ブロックを使って、枝の位置と角度を調整します。
Scratchのサンプルプロジェクトを開く
パソコンのWebブラウザで次のリンクからScratchのサンプルプロジェクトを開きます。このプロジェクトを改造していきます。
スクリプトを作成
フラクタルツリーのスクリプトを作成します。このスクリプトは再帰処理を含むため、自分自身を呼び出す処理が必要です。Scratchでは「ブロック定義」を用いることで、このような処理を実現できます。
ブロック定義とは
Scratchで複雑なプログラムを作る際に便利なのが、ブロック定義です。
ブロック定義は、一連の処理をまとめて、独自のブロックとして定義する機能です。他のプログラミング言語では、「関数」と呼ばれるものと似ています。
ブロック定義を使うことで、同じ処理を何度も繰り返す場合や、複雑な処理を分かりやすく整理することができます。
ブロック定義の作成手順
1. 「ブロックを作る」をクリック:

パレットの「ブロック定義」カテゴリにある「ブロックを作る」ボタンをクリックします。
2. ブロック名と引数を設定:
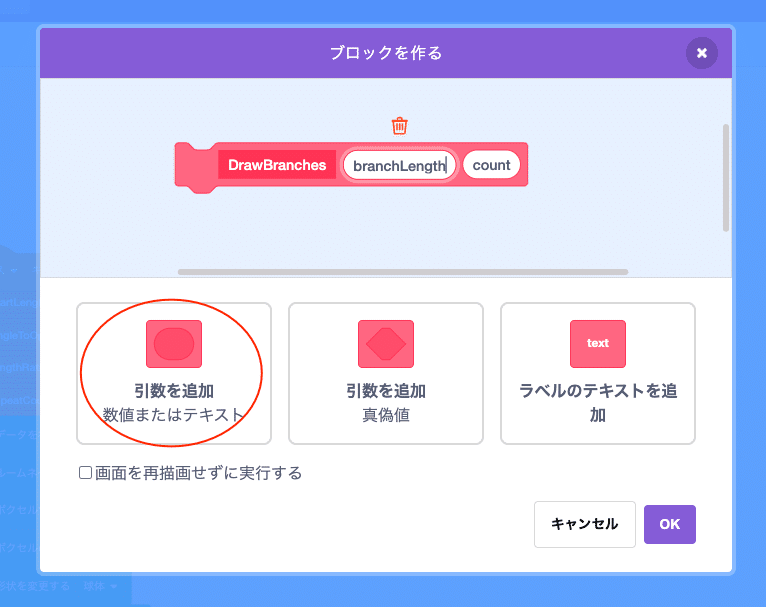
「ブロックを作る」画面が表示されたら、以下の設定を行います。
ブロック名: 作成するブロックの名前を入力します(ここでは「DrawBranches(枝を描く)」と入力します)。
引数: ブロックに渡す値を設定します(ここでは、「引数を追加」ボタンを2回クリックして、以下の2つの引数を追加します)。
branchLength(枝の長さ): 枝の長さを表す数値
count(カウント): 再帰の深さを表す数値
ブロック定義のスクリプトを作成
ブロック定義のスクリプトでは、3本のブランチ(枝)を伸ばす処理を実装します。
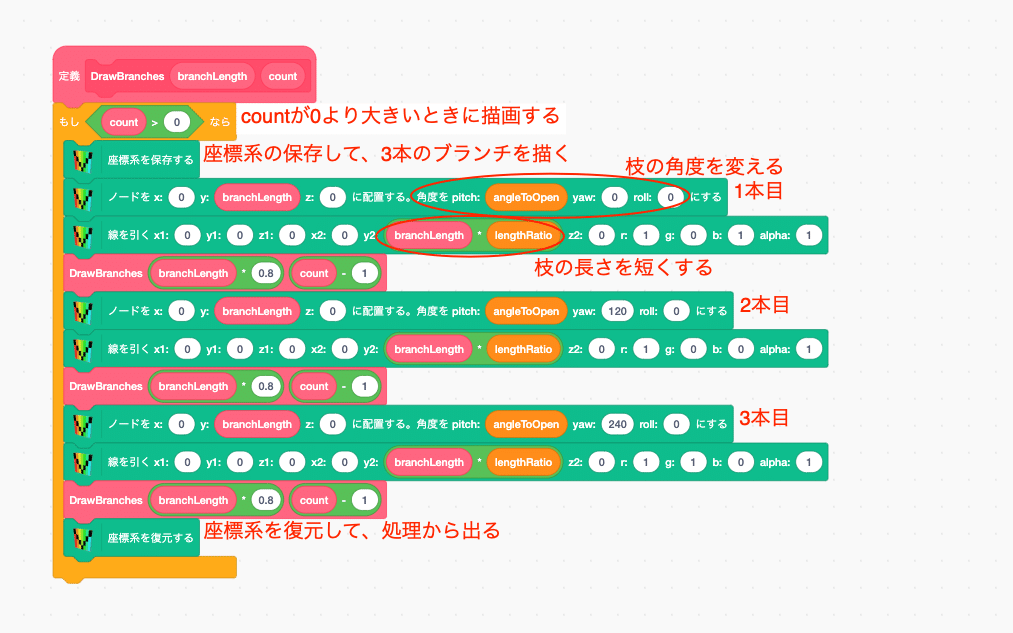
再帰処理の終了条件として、count が0になったら処理が停止するように、条件分岐ブロックを設定します。
「座標系を保存する」ブロックで座標系を保存してから、3本のブランチを描きます。座標系を保存しておくことで、ブランチの先端から新たに3本のブランチを伸ばすことができます。
枝の角度は、「ノードを移動する」ブロックで設定します。3方向に30度の傾きで新しいブランチを伸ばします。
枝の長さは、lengthRatio(= 0.8)を掛けることで処理を繰り返すごとに短くなっていくようにします。
3本のブランチを描いたら、座標系を復元して処理から出ます。
メインスクリプトを作成

メインスクリプトから、ブロック定義のスクリプトを呼び出します。
「フラクタルツリーの設定値」を設定します。この数値を変更することで、フラクタルツリーの形を変更できます。フラクタルツリーの設定値は以下のとおりです。
startLength - 初めのブランチの長さ
angleToOpen - ブランチの開く角度
lengthRatio - ブランチの長さを短くしていく比率
repeatCount - 繰り返し回数
ボクセルの形状を「球体」に変更します(ボクセラミングでは、ボクセルの形状を「立方体」「球体」「平面」の3つから選択できます)。
float コマンドを実行することで、精密な配置が可能になります。これにより、ほぼ真っ直ぐなブランチ(線)を描画できます。
「線を描く」ブロックで最初のブランチ(幹)を描いた後、DrawBranches ブロックを実行します。
以上で、スクリプトは完成です。実行してみましょう。
スクリプトの実行

フラクタルツリーは通常2次元で描かれますが、ボクセラミングでは3次元のフラクタルツリーを簡単に描けます。startLength などの「フラクタルツリーの設定値」を変更すると、フラクタルツリーの形状を変化させることができます。ぜひ試してみてください。
問題:3次元版のシェルピンスキーの三角形
図4のシェルピンスキーの三角形を立体にしてみよう!
挑戦してみよう!
シェルピンスキーの三角形は平面図形ですが、正四面体の面に貼り付けることで立体図形に変更できます。
sierpinski という名前のブロック定義を作成します。
シェルピンスキーの三角形を再帰処理を用いて実装します。
正四面体の面に貼り付けるため、位置と角度を調整してシェルピンスキーの三角形を3回描画します。
次回予告
次回は、いよいよ最終回!
これまで学んだことを活かして、オリジナルのボクセルアート作品作りに挑戦します。
お楽しみに!
ScratchでAR プログラミング入門シリーズ
ScratchでARプログラミング入門シリーズの一覧です。
第1回 プログラミングでARボクセルアートを作ろう!
第2回 繰り返しでボクセルの街を作ろう!
第3回 条件分岐でボクセルアートをもっと自由に!
第4回 ランダムでボクセルアートをもっと楽しく!
第5回 線を描いて、AR空間に立体図形を作ろう!
第6回 ボクセルで文字を描いて、AR空間に情報をプラス!
第7回 再帰処理でフラクタル図形に挑戦!
第8回 最終回 自分だけのARワールドをつくろう!
