
統計検定2級以上を目指して、階乗とガンマ関数を理解したい
はじめに
分析屋の小泉と申します。
前回は有意確率について2回に分けてじっくりと解説しました。
現状や実務上の問題点まで網羅しておりますので、是非ご覧ください。
今回は離散変数と連続変数から、階乗とガンマ関数の説明を行います。
ほぼ同時リリースで出したもう一本の記事では、最初の確率分布としてベルヌーイ分布を紹介しています。
こちらの記事の離散変数や階乗を理解することで、より考えやすくなると思います。
また、途中にも出てくる二項分布に向けた『組み合わせの数』に言及するため、是非一気に読んで理解を深めて頂ければと思います。
一方、ガンマ関数は統計検定2級レベルでは覚える必要はありません。
ですが、階乗と密接に関係する上に、様々な確率分布に採用されている関数です。
階乗と一緒に「こういうのがあるんだ」とだけでも知って頂き、もし準1級以上を目指すなら是非考え方まで理解したい内容です。
いよいよ数式が多用され、微分積分も多数出てきます。
今回提示する積分を解くことはあまりないのですが、統計学は数学と隣り合わせ(というか内包している)なので、数式が怖くて仕方ないと思わないでくださいね。
勉強していくと、いずれ物理学や天文学などの関連も見えてきて面白くなってきます。
古典統計学の歴史や奥深さに少しだけ触れながら、一緒に頑張っていきましょう。
離散変数と連続変数
まずは、基礎的な離散変数と連続変数について考えていきましょう。
離散変数は、数値と数値の間が離れている変数。
連続変数は、数値と数値の間にも区切りがない変数。
こう書けば分かる人には分かるのですが、初見だとちょっとイメージしにくいかも。
プログラマー的には、変数宣言において
離散変数・・・INT型、integer型
連続変数・・・FLOAT型、DOUBLE型
的なイメージです。これでも分かりづらいでしょうか?
ざっくり言えば、
整数しかないのが離散変数
小数点以下もあるのが連続変数
という感じです。
『無限に中間値が存在しない(=最小単位が存在する)』というのが実際の定義なんですが、これでも分かりづらい。
例えば、もの(人)を数えるとき。
「リンゴが2個あるよ!」とは言いますが、「じゃあ0.5個食べるよ!」とは言いませんよね。
「社員が283人いるよ!」とは言いますが、「来月3.3人増えるよ!」とは言いませんよね。
もの(人)を数えるときは、最小単位は1です。そして、1より小さい値(=小数点以下)を見ることはありませんよね。
もちろん、小数でなくてもよいです。
例えば千円札を考えてみましょう。
千円札1枚、1枚、2枚としか値は変化しません。
金額としては1000円、2000円としか変化せず、千円札だけで1500円は表せませんよね。
つまり、千円札での金額の最小単位は1000円で、それより細かくすることが出来ません。
このようにして、最小の単位同士で値が離れているとき、それより小さい値の目盛りが存在しない変数が離散変数です。
その逆、いくらでも値を細分化できるのが連続変数です。
「この木材の長さは3cmです」といったときに単位は1cmですが、
別に0.1cmや0.01cmの誤差があってもおかしくないし、
「3.1cmです」や「3.01cmです」と言っても問題ありません。
余談ですが、連続変数では「3cmです」と「3.0cmです」は全く意味が異なります。
「3cmです」は2.5cmや3.4cmだったとしても四捨五入している可能性がありますが、
「3.0cmです」は2.95cmから3.04cmを四捨五入しないと得られないからです。
すなわち、3と3.0は値としては同じでも、精度は全く異なります。
これが有効数字という考え方で、分野によって書き方は違えど非常に重要な概念です。
さて、話を戻します。
どうして変数のカテゴリをわざわざ解説するかというと、
確率は離散変数と連続変数で表し方が全く異なるためです。
離散変数では値が飛び飛びのため、確率の前提条件が少し緩かったり考えやすかったりします。
一方で、連続変数ではどんな値が入っても良いように確率を求めるために関数が用いられます。
例えば、1日2個生産するプロセスの場合、在庫は2個ずつ増えていきます。
『個』はものの数え方なので、離散変数ですね。
日付(x日目)時点での在庫数yを表とグラフに表すと、次のようになります。

当然ですよね。
ここで、上司に「1.5日目の在庫数は?」と聞かれても「1日目は2個、2日目は4個です」としか言えません。
日数も離散変数だから、1.5日目という概念すらありません。そんなこと言われても勘弁してほしいですよね。
でも、棒グラフではなく折れ線グラフにするとこうなります。
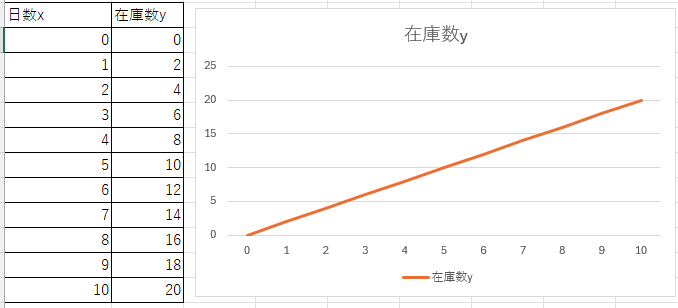
どうでしょう。
これなら上司の「1.5日目の在庫数は?」という質問にも、
横軸が1.5のときの縦軸を見ればよいので、「3個です」と回答できてしまいます。
・・・本当にそれで良いのでしょうか?
上司の指示が「1.5日目」だったから割り切れましたが、1.3日目だったらどうしますか?
「在庫は2.6個です」と答えますか?
2個はともかく、まだ生産が終わっていない0.6個分を報告する必要があるのでしょうか?
そもそも、「在庫が0.6あります」って意味分からなくないですか?
これが、離散変数と連続変数が決して同じものとして表せない理由です。
確率変数も表し方が異なると先に話しましたが、こういう理由なんですね。
再度おさらいです。
「それ以上細かくできない数値の桁がある」のが離散変数で、
「無限に桁数を細かく考えることが出来る」のが連続変数です。
そのため、離散変数は「棒グラフで表すのが適切」といえますし、連続変数は「折れ線グラフが適切」といえるかもしれません。
なお、「厳密に考えると連続変数も離散変数じゃない?」という話は無しにしてください。
有効数字の解釈によって、どんなに細分化してもどこかの桁数に落ち着くのは必然ですが、
問題は連続変数とみなすか、離散変数としてみなすかという議論になります。
階乗ってなんだろう
次に階乗について考えます。
階乗とは、「1からnまでの整数の積である」そうです(wikipediaより)。
例えば、『3の階乗は?」と言われたら、
3✖2✖1=6
と答えれば正解です。
『8の階乗は?』といわれたら、
8✖7✖6✖5✖4✖3✖2✖1=40320
・・・計算、めんどくさいですね。
大丈夫です、実際はもう少し簡単です。
統計検定において、階乗を最も利用するのは二項分布でしょう。
次々回以降にきちんと解説しますが、二項分布では次の式を覚える必要があります。

馴染みがない人は卒倒しそうな数式ですが、
実はこの中の!(びっくりマーク、エクスクラメーション)は階乗を表しています。
「『実際はもっと簡単です』とか言ってたくせになんだこのめんどくさい公式は!」
とお怒りの方もいるかもしれません。落ち着いてください。
!は階乗を表しますので、n!は以下のように計算されます。

もう少しかみ砕くため、実際の数字を入れてみましょう。
先の『8の階乗』、すなわち『8!』を計算すると、

となります。
数式で表すと面倒くさいですが、実際に値を入れてみると意外と簡単なんですね。
さて、階乗に慣れた上で二項分布の公式に戻りましょう。
やっかいなのは$${{}_nC_k}$$なので、ここだけ部分的に取り出してみます。

うーん、階乗はなんとなく分かったけどこの式の意味が分からないですね。
これも式だと分かりづらいですが、実際に計算すると意外と簡単です。
例えば$${n=8}$$,$${k=5}$$と代入してみましょう。
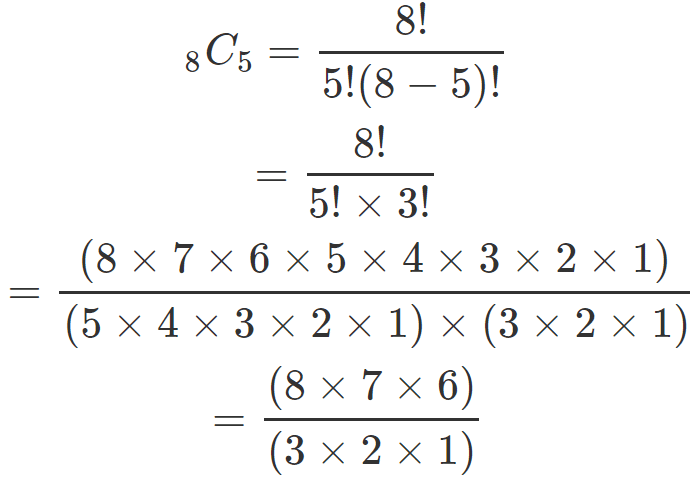
どうでしょう。数字はいっぱい出てきましたが、最終的には約分することで少なくなりました。
そして、最後にはこうなります。

整数でまとめることができました。
階乗が出てくる式は、『実際に計算するならそんなにめんどくさくないのに、公式だけ見るとなんかめんどくさそう』の典型です。
とにかく、階乗の基礎と実際の計算方法を覚えましょう。
実際にやってみれば簡単です。
なお、そもそも$${{}_nC_k}$$についてはいずれ解説します。
今は階乗は「その値を-1して全部かけていくんだ」と覚えて頂ければ結構です。
階乗とガンマ関数
ここまで、離散変数と連続変数、そして階乗について考えてきました。
ここで、階乗の定義をよく見てみましょう。
階乗とは、1からnまでの整数の積である
そうです。整数しか登場しないのです。
ということは、小数点以下の値が入るようなものには適用できないということです。
すなわち、離散変数にしか適用できず、連続変数には適用できません。
「まあそういうものだろ」と思いましたか?
しかし、かの有名な数学者、オイラーさんは言いました。
「俺は連続変数でも階乗したい」
棒グラフだけでなく折れ線グラフも使いたくなったんですかね?(適当)
学生時代の私もそうでしたが、機会が限定されるとそれ以外のことを考えたくなってしまいます。
ルールを守れと言われたらギリギリを攻めたくなるタイプの人です。
とはいえ、階乗はnが大きくなると次のような形を取ります(エクセルではFACT関数で簡単に求められます)。

nが大きいほど一気にyも大きくなります。
これを連続変数にも当てはめるにはどうするべきでしょうか?
オイラーさんは考えました。
「1から2に増えたときは1→2。2から3に増えたときは2→6。ということは、次の値の変化量を予測できれば、中間の値でも求められるはず」
もう少しかみ砕くと、
整数での離散変数なんだから、nの増え方でyがどれくらい変化しているかわかれば、その間・・・小数点以下の値が加わっても折れ線グラフが書けるはず。
つまり、折れ線グラフで書くとカクカクだった階乗のグラフを、「nが増えればyがどれくらい増えるか」を予測できれば、

↓こんな感じで、整数でない値も求められて曲線で表せるかもしれない!

「nが増えればyがどれくらい増えるか」とは、nによるyの変化量ですね。
ということはつまり?
よく思い出してみましょう。これまでの私のブログを見ると、実は第1回に解説しています。
そう、微分です。
階乗がどのように変化するか、変化量が分かれば微分関数として表せる。
関数として表せるということは、小数点以下の値が入っても答えが出せる。
よって、nが連続変数であってもyが求められる。
逆に、微分で求められた関数を積分すれば元の値に戻る。
ということは、微分された関数を整数以外のどんな値でも定積分すれば値が求められるはず。
このように考えたオイラーさんは、階乗の値の変化量を考えました。
微分は変化量を求める問題です。
ですから、nのときとn+1のときのyの値(y(n)、y(n+1))をそれぞれ求め、
それぞれの差を求めて、「nが1増えたらyはいくら増えるか(=yの変化量)」を調べ、これを関数で表しました。
実際に整数で階乗を求めたときのyの変化量dyを表に求めました。

ですから、dyを関数として表せれば、積分することでyの値・・・nの階乗を連続変数にも適用できるはず。
さて、オイラーさんは見事にこれを関数として1つの式に表し、ガンマ関数と呼ばれるようになりました。
次のような式です。

はい、数式アレルギーの方はこの辺で離脱すると思います。
「$${\Gamma}$$って何だよ!なんて読むんだよ!」(ガンマと読みます)
「なんで∞(無限)が出てくるんだよ!」
「eってなんだよ!」
「tとかdtってなんだよ!」
そう思われたかもしれませんが、いったん落ち着いてください。
実際に統計学を利用する場合、これを解くことはまずありません。
一応数Ⅲまでの知識があれば解くことは出来ますが、重要ではありません。
例えば、3の階乗は

ですが、ガンマ関数を用いてn=3で求めても

として求められます。
例えば、本来求められないはずの0.5の階乗も、

として、計算で求めることが出来ます。
なお、「どうして円周率$${\pi}$$が出てくるの?」という話は考えないでください。
ここを求めるのに数百年分の数学の歴史が詰まっています(導出は本記事の最後に補足として載せておきます)。
このようにして、本来離散変数にしか適用できなかった階乗が、関数としてどんな値でも求められるようになったのが重要です。
先に提示した二項分布は離散変数について様々使える万能な確率分布であることをド・モルガンやラプラスなどの偉大な数学者が見つけたのですが、連続変数には使えないというデメリットがあります。
よって、連続変数の確率分布にはガンマ関数が不可欠となるわけです。
次回以降は確率分布について詳しく見ていきますが、階乗とガンマ関数が何度も出てきますのでそのためのスタートとなる内容でした。
終わりに
今回は離散変数・連続変数、そして階乗とガンマ関数について紹介しました。
具体的に理解しないと何のことだか分からないかもしれませんが、次回以降の確率分布でこれらは出てきますので第一歩としてご紹介しました。
いよいよ数式が増えてきますので、アレルギーが出ないよう徐々に慣れていきましょう。
アレルギーがない方は是非この後の補足の計算も頑張ってみてください。
補足(ガンマ関数による階乗の導出)
実際にガンマ関数を用いて階乗を求めてみましょう。
3の階乗を求めてみます。

3の階乗を求めるならn=3のため$${\Gamma(3+1)=\Gamma{4}}$$を求めれば良いので、実際にガンマ関数から求めてみましょう。

部分積分を利用して、


ちょっと大変ですが、$${\lim_{n\rightarrow0}{-t^{3}e^{-t}}=\lim_{n\rightarrow\infty}{-t^{3}e^{-t}}=0}$$が成り立つため(ここでいうnは自然数なら何でもOK)、最終的には

となりました。
$${3!}$$の値と$${\Gamma{3+1}}$$の値が一致することが分かりました。
どんな整数の値でも、最終的には$${\int_{0}^{\infty}{e^{-t}}dt=1}$$に帰結するため、結果的に階乗と同じ計算をしています。
では、nが整数でない・・・例えばn=1.5ならどうでしょうか。
1の階乗は1ですが、1.5の階乗は意味が分からないですよね。
なお、以下のような階乗(ガンマ関数)の性質上、$${-0.5!}}$$が求められればあとは計算が簡単です。
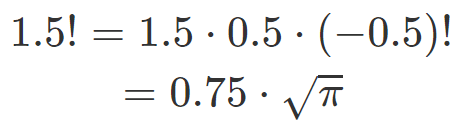
ほかのどんな値でも、階乗は1を引いた値の積となるため、-1〜0の範囲の階乗が分かれば、理論上どんな値の階乗も求めることが出来ます。
それでは、問題の$${(-0.5)!}$$を求めていきます。
なお、ここからは解説し出すとそれだけで記事が一本書けるので、計算過程だけ残します。

であるから、$${x=-0.5}$$を代入し、

$${t=x^2}$$とし、置換積分を用いて

となるため、

となる。
一度この積分について考えるため、

とおく。
$${x}$$だけでなく$${y}$$方向(二次元)への拡張を考慮し、$${I}$$を二乗して

フビニの定理から

さらに、極座標変換

を行い

ここで、$${u=r^2}$$として再度

として置換積分を行い、

よって、$${I^2=\pi}$、すなわち$${I=\sqrt\pi}$$が得られるため、

が求められるため、

となりました。
以上から1.5の階乗が求められました。
なお、割り切れない値(無理数)のガンマ関数はどうするの?などと考えた方は数学科向きなのでぜひ頑張ってください。私は考えたくないです。
途中に出てきた$${I=\sqrt{\pi}}$$はガウス積分と呼ばれ、いずれ解説する正規分布と同じ計算をしています。
ガウスさんというこれまた偉大な人が、「天体の動き方ってこんな感じじゃないかなあ」という考えで発表した天体運動論にて、このガウス積分が登場します。
また、そもそもの基礎となる微分・積分はニュートンが、$${e^{x}}$$という指数関数やネイピア数は、ベルヌーイやまたもやオイラーが発見しました。
このように、統計学は物理学や天文学とも非常に結びつきが強いのです。
というより、順序としてはガウスの天文学がこれらを参照したからこそ統計学は生まれた・・・みたいな歴史の話も、またどこかでしていきたいですね。
ここまでお読みいただき、ありがとうございました!
この記事が少しでも参考になりましたら「スキ」を押していただけると幸いです!
これまでの記事はこちら!
株式会社分析屋について
弊社が作成を行いました分析レポートを、鎌倉市観光協会様HPに掲載いただきました。
ホームページはこちら。
noteでの会社紹介記事はこちら。
【データ分析で日本を豊かに】
分析屋はシステム分野・ライフサイエンス分野・マーケティング分野の知見を生かし、多種多様な分野の企業様のデータ分析のご支援をさせていただいております。 「あなたの問題解決をする」をモットーに、お客様の抱える課題にあわせた解析・分析手法を用いて、問題解決へのお手伝いをいたします!
【マーケティング】
マーケティング戦略上の目的に向けて、各種のデータ統合及び加工ならびにPDCAサイクル運用全般を支援や高度なデータ分析技術により複雑な課題解決に向けての分析サービスを提供いたします。
【システム】
アプリケーション開発やデータベース構築、WEBサイト構築、運用保守業務などお客様の問題やご要望に沿ってご支援いたします。
【ライフサイエンス】
機械学習や各種アルゴリズムなどの解析アルゴリズム開発サービスを提供いたします。過去には医療系のバイタルデータを扱った解析が主でしたが、今後はそれらで培った経験・技術を工業など他の分野の企業様の問題解決にも役立てていく方針です。
【SES】
SESサービスも行っております。
