
統計検定2級に向けて、ベルヌーイ試行と組み合わせの数(nPrとnCr)を考える
分析屋の小泉と申します。
今回は2本同時リリースとして、一本は「離散変数と連続変数、階乗とガンマ関数」について、
そしてこちらではベルヌーイ試行と組み合わせの数について
一気に解説したいと思います。
どちらも相互に関係する内容ですが、文量が多くなって大変だったので分けました。
こちらの記事では、個人的に苦手だった組み合わせの数について解説しますが、
途中から離散変数や階乗が頻繁に登場します。
そのため反対の記事で解説している内容を読むと理解が深まるかも知れません。
一方で、後半にガンマ関数というめんどくさいものにも触れており、そこは読み飛ばしても構いません。
統計検定2級レベルであれば必須ではない内容のため、
まずは離散変数と階乗が理解できたらこちらの記事も読んで頂ければと思います。
ベルヌーイ試行
世の中には様々な事象が仮定されており、確率によってその試行における発現しやすさが表されます。
ここで、結果を2択で表す試行をベルヌーイ試行と言います。
一番よく言われるのはコインの裏と表。出る面は2択です。

ですが、コインのように、結果を2択に限定することがマストではありません。成功と失敗、trueとfalseを後から定めてしまえば、これもベルヌーイ試行と言えます。
例えば、「サイコロの目で5が出るか」という試行。
サイコロを投げるという試行は6面のうち1面が出る・・・6択の試行です。
しかし、「5が出た=成功」と「5が出なかった=失敗」と置き換えれば、二択で考えることができます。
プログラミング的には、if~else…文といえるでしょう。
case文だかselect文ではなく、2択と捉えらればそれはベルヌーイ試行と言えます。
そのため、複数パターンの結果が予想される場合、成功と失敗に分類しておき、
それぞれの確率を成功確率・失敗確率として合算しておくことで、擬似的にベルヌーイ試行と解釈することができます。

さて、ベルヌーイ試行の成功と失敗確率を考えてみましょう。確率の総和は1という公理、そして2択ということから、
成功する確率がpであるとき、成功しない(失敗する)確率は1-pで表されます。
事象をkとして表し、k=0のとき失敗、k=1のとき成功を表すとしてみると、次の式でまとめられます。
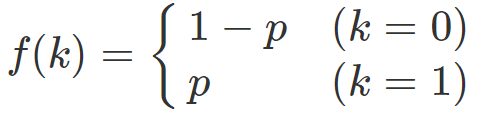
式でまとめるとちょっと気持ち悪いですね。
でも、成功のときkに1を代入、失敗の時にkに0と代入すれば確率が求められる、ということを表しています。
このように、「このパターンのときこの確率になる」ことを式(関数)で表したものを確率質量関数といいます。
パターンという通り整数のみのため、離散変数の確率を表す関数ですね。
今回で言うと、ベルヌーイ試行であるから、パターンは2択しかありません。
そのため、2択のどちらかの結果しか得られず、どちらもちょうどいいぐらいの結果が出るとは言えません。
「結果は成功を表す1ですか?失敗を表す0ですか?」と言ってるんです。
「結果が0.4になる確率は?」と尋ねられたら私は怒ると思います。

このように、ベルヌーイ試行の結果が従う確率分布のことをベルヌーイ分布といいます。
わざわざ成功と失敗を0と1なんて数字に当てはめたのは、式(関数)であらわされる確率なら分布と呼べるからです。呼ばせてほしいんです。
「2択しかない分布ってなんか違和感がすごい」←慣れてください
ちなみに、ベルヌーイ分布は以下のような書き方もできます。実際にk=0もしくはk=1を代入すれば同じ結果になります。

これ、見た目は面倒くさいし覚えるのも嫌になりますが、kが0でも1でもない中間の計算もできてしまいます。
連続変数に適用できる、という意味で階乗とガンマ関数の関係に似ているかも知れません。
組み合わせの数
ベルヌーイ分布では大事な前提を抜いていました。
それは、「試行は1回しか行わない」ということです。
試行を1回しかやらないから、結果は成功と失敗の2択しかないのです。
では、複数回試行する場合はどうなるでしょうか。
これを考えるために、高校数学で習う組み合わせの数について解説します。
まずは、ベルヌーイ試行の各回を、あえてA,B,C,D,E・・・と呼んでみます。
各回はすべて同じ操作ですが、何回目の試行なのかわかるためにあえてそうさせてください。
まずは、3回のベルヌーイ試行の順番が何通りあるか考えてみましょう。
最初にA,B,Cの3択ですが、次は選ばれなかった残りの2択ですし、最後は今まで選ばれなかった1択しかありません。
そのため、全パターンを書き出すと
ABC,ACB
BAC,BCA
CAB,CBA
よって、計算で求めるなら、3*2*1=6パターンあるといえます。

ということは、階乗ですね。同様に、5回の試行でも5*4*3*2*1=120パターンあるといえます。

それでは、5回の試行のうち3回成功する組み合わせは何パターンあるでしょうか。
5回のベルヌーイ試行のパターンは最大で120通りです。
仮にAが成功した場合、2回目の成功はB,C,D,Eのどこで出てもよいことになります。
仮にAが失敗した場合、1回目の成功をB,C,Dのどちらかで出すことが必須となります。
このように考えると、成功パターンを考えるのはちょっと複雑そうですね。

5回の試行をA,B,C,D,Eと当ててみると、1回目の成功はA~Eの5択から選べますが、2回目の成功は選ばれなかった4択から選び、3回目の成功は更に減って3択から選ぶことになります。
しかし、5回の試行で3回を成功させる組み合わせなので、3択まで進んだらそれ以降は考える必要がありません。
よって、5*4*3で計算を止めて良いということになります。
全パターンを求める5*4*3*2*1に対して、必要なパターンは5*4*3で求めることが出来たため、2*1分が不要になったとも言えます。

すなわち、試行する回数の階乗で全パターンを求め、成功しない(失敗)回数の階乗で割れば組み合わせの数が求められます。

ここまで着いて来れたでしょうか。
かなりややこしく、自分は学生時代にここで躓き統計学を諦めていたので、自信を失わないでください。もう少しだけ頑張りましょう。
先の組み合わせの数を求める際、全パターンから成功しない回数の階乗を割りました。
これで得られるのは、試行それぞれを全くA,B,C,D,Eの別物として扱い、どの試行がにどの順で成功するかを考えた組み合わせです。
「最初にAが成功したら2回目の成功はB~Eのどれかになる、選択肢が狭まる」ということからも、どの試行が成功するか・いつ成功するかまで考えていました。
言い換えれば、A~Eの中から3回成功する試行を抜き出し、順番に並べる組み合わせまで考えていました。
成功した三回の試行を並び替える全パターンは、最初に示したとおり3の階乗で表せます。
実際の状況では並び替えることはあまりせず、「5回の試行をA,B,C,D,Eと置き換えたときどれが成功するか?」しか興味がありません。
仮に試行A,B,Cが成功したら、その順番はABC、ACB、BAC、CBA、CAB、CBAのどれであったとしても1パターンとして扱われます。
そのため、成功した試行回数の階乗個・・・今回で言うと、3回成功を考えているので3*2*1の6パターンを1つとして考えることになります。
よって、組み合わせの数を求めたら、更に成功した回数の階乗で割ることで、ようやく順番を考慮しない成功した試行のパターン数を求めることが出来ます。

以上の説明から、組み合わせの数は2種類あり、順列を考えているものと順列を考えないものがあります。
順列は$${{}_nP_{r}}$$、組み合わせは$${{}_nC_{r}}$$として数学的に表されますが、
自分はこれがあまりにも苦手だったので、社会人になってからは
全パターンは階乗!
着目しない外れ回数の階乗で割ると並べるときのパターンが出せる!
更に着目する当たり回数の階乗で割ると順番も気にしないパターン数が出せる!
と覚え直しました。
式や文字だけで覚えようとすると数式アレルギーを起こしていたので、フィーリングで覚えていきましょう。
組み合わせの数とベルヌーイ試行
先にも述べたように、組み合わせの数はベルヌーイ試行が元になっています。
当たりや外れ、成功と失敗の二択で考えていましたが、もちろん「着目するもの」と「着目しないもの」の二択で考えてもベルヌーイ試行と言えます。
組み合わせの数によってベルヌーイ試行での試行回数と成功回数からパターン数が割り出せるため、
ベルヌーイ分布の確率質量関数と組み合わせて、複雑な試行回数・成功回数での確率分布も求められるようになります。
それがいわゆる二項分布なのですが、また次回以降に説明したいと思います。
終わりに
今回はベルヌーイ試行と組み合わせの数についての説明を行いました。
一時期の自分が躓いて理解を拒んだ内容なので、当時の自分に教えるつもりで可能な限り丁寧に記載したつもりです。
あまり組み合わせの数の問題は統計検定2級では出なかった気がしますが、3級では出るのでしょうか。
少なくとも常識過ぎて2級以上では「触れなくても分かってるでしょ」ぐらいの内容なのかもしれませんが、
曖昧なまま式だけ覚えるのも微妙ですし、レベルが上がるとCとかPすら書かなくなるので、計算方法だけでもすらすら言えるようにしたいところですね。
ここまでお読みいただき、ありがとうございました!
この記事が少しでも参考になりましたら「スキ」を押していただけると幸いです!
これまでの記事はこちら!
株式会社分析屋について
弊社が作成を行いました分析レポートを、鎌倉市観光協会様HPに掲載いただきました。
ホームページはこちら。
noteでの会社紹介記事はこちら。
【データ分析で日本を豊かに】
分析屋はシステム分野・ライフサイエンス分野・マーケティング分野の知見を生かし、多種多様な分野の企業様のデータ分析のご支援をさせていただいております。 「あなたの問題解決をする」をモットーに、お客様の抱える課題にあわせた解析・分析手法を用いて、問題解決へのお手伝いをいたします!
【マーケティング】
マーケティング戦略上の目的に向けて、各種のデータ統合及び加工ならびにPDCAサイクル運用全般を支援や高度なデータ分析技術により複雑な課題解決に向けての分析サービスを提供いたします。
【システム】
アプリケーション開発やデータベース構築、WEBサイト構築、運用保守業務などお客様の問題やご要望に沿ってご支援いたします。
【ライフサイエンス】
機械学習や各種アルゴリズムなどの解析アルゴリズム開発サービスを提供いたします。過去には医療系のバイタルデータを扱った解析が主でしたが、今後はそれらで培った経験・技術を工業など他の分野の企業様の問題解決にも役立てていく方針です。
【SES】
SESサービスも行っております。
