
大学数学の入口に立ったあなたへ 〜数学編〜
こんにちは、微小です。
この記事を読んでいるということは、無事に大学に合格し、新たな気持ちで数学を学ぼうとしていることでしょう。合格おめでとうございます!
僕も高校生のころから数学科を志し、大学で本格的な数学を学ぶことを楽しみにしていました。実際、数学科はとても楽しいところです。高校生では知りえなかった世界が大きく広がっています。
僕は今大学3年生になろうとしています。そこで、実際に数学科に2年間在籍してみて感じた、僕が数学科に入る前に知りたかったこと、例えば大学数学とは何か?どう学ぶのか?何が大切か?ということなどを、経験をもとに伝えていけたらいいなと思います。
そして、この記事を読んで下さった数学科新1年生の方々が、より良い大学生活、そして数学ライフを送れることを願っています。駄文ではありますが、どうぞ最後までお付き合いください。
0節 この記事について
この記事は、主に数学科に所属する大学新1年生に向けた記事となっています。その他にも、大学数学を学びたい理学部の方などにもおすすめです。この記事が、誰かの何かのヒントになることを願っています。
1つ断っておく必要があります。僕自身、特段数学ができるわけでもなく、時には高校数学まであやふやな、こんな偉そうな記事を書けるような人ではないということです。有識者の方からすれば、間違ったことが平然と書いてある、と思われるかもしれません。間違い等ありましたらご指摘ください。
すなわち、僕自身も皆さんと同じ立場にいます。僕は、数学とはどんなもので、どう学ぶのか、など数学観について模索をしている最中です。時が経てば、この記事の内容が変わるかもしれません。ですので、あくまでも参考程度に、ご自身の大学の方針・スタイルにあったように解釈していただけると嬉しいです。
さて、この記事では、大学数学はどのようなものか、何を学ぶのか、どう学べばいいか、といった技術的な側面について、書きたいと思います。実際に数学科に入ってみて、色んな人から影響を受けた結果としての、今の僕の数学の考え方を共有したいと思います。
1節 高校数学と大学数学の違い
1.0 好きという気持ち
まず、高校数学、大学数学に限らず、「数学が好き」という気持ちは、数学科であるからには絶対に忘れてはいけません。
「正直数学は得意じゃないけど、数学が好き。大学でもっと数学を学びたい!!」という強い心意気があれば、きっと大丈夫でしょう。僕だって、旧帝の人と比べたら数学のセンスの欠片もありませんが、数学は大好きです。周りの友達も「数学が大好き」とはっきり言える人ばかりです。
数学に限らずですが、「楽しむ心」が一番大切だと思います。「折角数学科に来たのですから」数学科でしか得られないものを学んで行きましょう。
1.1 高校数学と大学数学の違い
(この記事では、教養数学と区別して、専門数学のことを大学数学、数学と呼びます。)
皆さんの中には、数学科を志望した理由として「高校数学は計算楽しいし、テストも入試問題も得意だから大学数学もいけるだろう」という方がいるかもしれません。もちろんそれはそれでいいのですが、残念ながら、その考えは大学数学ではあまり通用しないでしょう。
高校数学と大学数学は思考の仕方がまるで違います。学ぶとわかりますが、高校数学が大学数学の簡単お試しコースだったのではないかと思えるくらい、大学数学はとても難しいです。
大学数学は「専門数学」、すなわち一般の数学者が扱っている数学そのものです。そのため、高校では授業を適当に聞いても何とかなっていたという人も、大学数学ではそうはいきません。数学は知識と思考の積み重ねでできている学問ですから、わからなくなると一瞬で沼にはまってしまいます。
寄り道として、某予備校講師の某動画内で、個人的に感銘を受けた文を載せておきます。
所詮手際よく解ける入試問題という箱庭の中でしか生きていけない解答に過ぎないんだ……
この通り、高校数学では確実な答えというものが保証されています。しかし、大学数学では、基本的に個人での戦いです。定義・証明を読んでもわからない、演習問題でつまずいたとき、答えを見ても何を言っているかわからない、そもそも巻末に答えがついていないなど、わからないことに多く突き当たります。しかし、それを最終的には独力で理解していかなければなりません。
そのため、高校数学の何倍も「自分で文章を理解し、自分で考える力」が求められます。大学数学は「とにかく考えて考える」そして理解する。問題を解くための方法を学べばいい受験数学とは全く異なります。
もちろん、大学数学は高校数学の経験を前提に話が進められます。しかし、高校の授業のような、問題が解ければヨシ!というのは違います。大学数学をガチでやりたいという方は、高校数学のやり方とはお別れをしましょう。(得た知識とはお別れしないでください)
以下に、一部参考にさせて頂いた記事を載せておきます。
では、具体的には何が違うのか?調べれば色々出てくると思いますが、やはり2点「厳密性の高さ」と「抽象度の高さ」だと思います。
1.2 厳密性の高さ
数学の醍醐味は、やはりその厳密性でしょう。前述のとおり、高校数学は専門数学と比べて厳密性に欠きます。
例えば、極限、積分、ベクトル、確率、さらには関数、実数、四則演算など、これまで当たり前に使っていたものをはじめ、数学の議論で使うものは、全て厳密な定義があります。高校数学は専門数学ではないので教わらなかっただけで、専門数学では全てを丁寧に定義します。(3.1を参照)
そして、数学には「漏れ」がありません。基本的に、数学用語を使うときは必ず前に定義が書かれていなければならず、定理の証明にある命題/主張を使うときは、必ず前に証明が書かれていなければなりません。
もちろん、定義の中で使われている数学用語にも定義があって、さらにその定義の中に……(これの最終到達点が公理です)というように、どんどん細かく厳密にしていくのも、数学の営みです。大学では、新たな概念を定義して、様々な定理を証明していくことになります。この流れが楽しいのです。
また、数学の議論・展開は、全て''数学語''と数理論理を用いて行われます。1つの議論のミスが証明の破綻につながってしまうこともよくあります。後述しますが、いかに''数学語''と数理論理が適切に扱えるかが、大学数学において厳密な議論をする上で非常に重要になります。
1.3 抽象度の高さ
数学のもう一つの醍醐味は、その抽象度の高さでしょう。
学部の最初の方はまだすんなりと理解しやすい(それでも難しい)ですが、専門性が高まるにつれて「これはいったい何をしているんだろう……」「参考書の言っていることがまるでわからん」となっていきます。
例えば、高校では、考える関数や集合が問題で明確に与えられ、かつ計算がしやすいことが多かったと思います。しかし、大学数学では、その抽象度の高さゆえ、ほとんどの場合、具体例・具体的イメージが出せないことがほとんどでしょう。最初から$${n}$$次元で考えて、あとから$${n}$$に2や3を入れればそれで済むよね、という発想です。関数は$${f}$$、集合は $${G}$$と与えられるだけで、具体例は一通りの定義や定理の証明が終わった後に示されることもあります。
抽象化するということは、「この条件を満たすものなら何でも適用できるようにする」ということです。ある定理を証明したとして、では具体例として何か挙げてくださいと言われても、「条件」を満たすものが中々見つからないこともあります。「数式が言ってることだからそうなんだろう」というようなことが起こります。
自論ですが、よく「数学力は国語力」だと思っています。証明や主張を丁寧に正しく読み、行間を適切に考えて埋める、まさに国語の読解問題に似ていると思いませんか。国語力がなければ、正確に主張を読み取ることができません。さらにそこに論理が入ることで、より複雑になっていきます。
と、まあここまで怖がらせるようなことを言ってきましたが、でも大丈夫!最初に述べた通り、数学が好きという気持ちがあればOKです。時間をかけてゆっくり進めればいいのです。周りを気にする必要はありません。
では次に、大学数学についてほんの少し紹介しましょう。
2節 大学数学は何をいつ学ぶのか
2.1 大学数学は何を学ぶ?
高校数学では、いろいろな分野を学んできました。薄々気づいているとは思いますが、中高の数学は、大雑把に「数と式」「関数」「図形」「確率・統計」に分けられていると思います。
(大学)数学は、主に「代数」「解析」「幾何」「応用数学」の4分野に分かれます(諸説あり)。各分野はとても広く細かく深く、相互に関連しあっています。数学分野の地図は、以下のツイートが分かりやすいと思います。
数学全体の分野の構造を俯瞰する一覧や“地図”みたいなもの、ありそうで意外と見かけないので自分で作ってみました。 pic.twitter.com/Qkw7z8PgHB
— 佐久間 (@keisankionwykip) July 6, 2022
また、弊学のパンフレットに載っていた図が分かりやすかったので載せておきます。(ボケててすみません)
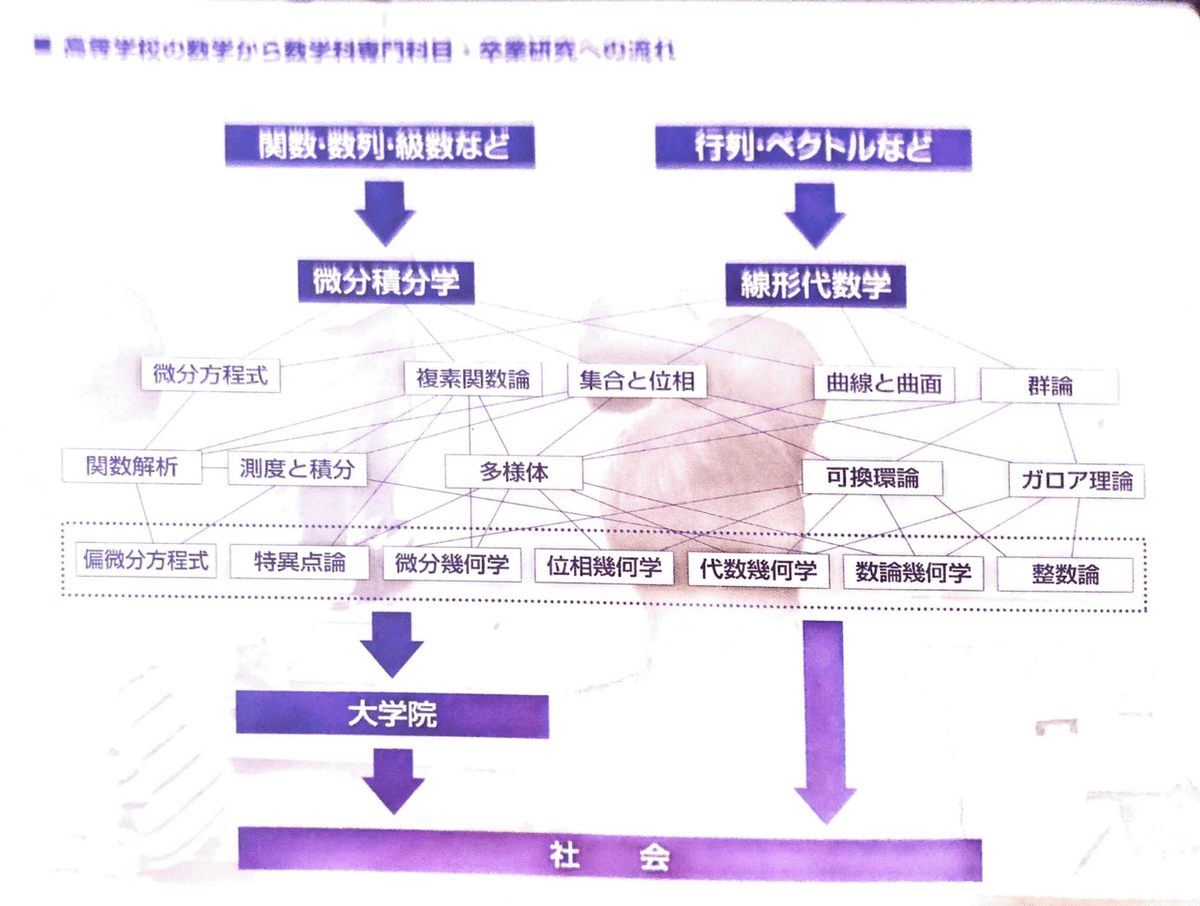
学んでいくうちに、自分の興味のある分野が見つかるといいですね。
2.2 各分野をいつ学べばいい?
2.1では大学数学の分野を見てきました。では、これらをどのように(どのような流れ/順序)で学べば良いのでしょうか?
結論から言うと、大学のカリキュラム、大学で履修する順で十分だと思います。特別、急いでやらないと不利になるとか、そういった様なことは基本的にありません。それならば逆に、1,2年生の段階では自分が興味を持った分野を積極的に学習しても良いと思います。
ちなみに、僕の大学での履修順は、図Aの1段目(微分積分学・線形代数学)を1年次に、2段目(微分方程式・複素関数論 etc.)を2年次に、3段目を3年次に……と学びます。恐らくどの大学でも、学習時期は違えど大方この流れだと思います。
それより、学んだことを忘れないよう、復習することも忘れないようにしましょう。数学は、様々な分野が相互に関係しています。つまり、違う授業で学んだことがまた違う授業で活かされるため、そうなったときにすぐ知識が引き出せるよう、復習が必要なのです。
2.3 論理・集合・写像は1番初めに学ぶべき!
ここでは自論を述べさせていただきます。1年次に微分積分学・線形代数学を学習しますが、何より先に論理・集合・写像について知っておいたほうが確実に良いでしょう。論理・集合・写像は数学の根幹であり、講義や参考書で当たり前のように使われるものですので、知っておくべきです。
ここでは、埼玉大学の福井先生の著書をお借りして紹介します。
春休み、何をすればいいか迷っている方は、とりあえず以下のテキストの27ページまでを一通り読んでおくことを強くおすすめします。
「数学科に入ったら読む本」福井 敏純
http://www.rimath.saitama-u.ac.jp/lab.jp/Fukui/lectures/intro.pdf
(記事を書くにあたってテキストを開いてみたら、はじめにのところに僕の言いたいことが書いてありましたね。そっちもぜひ読んでください。)
2.4 何を使って学べばいい?
さて、数学の学習に欠かせないものの一つに、参考書がありますね。図書館に行くと、様々な種類の本があって、何を選べばいいのかわからなくなってしまうかもしれません。
個人的には、講義(授業)で参考図書が示されている場合は、それに従うのが最善だと思います。何しろ先生方が薦める本ですから、ほぼ間違いはないでしょう。
参考図書が示されなかった場合は、自分で見つける必要があります。是非、一度は図書館に行って、どんな本があるかを自分の目で確かめてみるのもいいと思います。数学書は高いですから、積極的に借りてみましょう。
参考までに、僕が薦める参考書をまとめた記事を載せておきますのでご活用ください。
3節 大学数学の学び方・コツ
ここまで、大学数学の概観を紹介しました。では、具体的にどのような点を意識して勉強すれば良いのでしょうか?幾つか思う点を挙げてみました。
3.1 大学数学は定義が重要
皆さんは、定義や定理という言葉を聞いたことがあると思います。あやふやなときは、以下の記事が参考になりますので読んでみてください。
定義は、定期試験では書くだけで点がもらえるほど、逆にいえば覚えていないと正しい議論が何もできない非常に重要なものなのです。定義は、数学の議論をする上での約束事ですから、間違えて覚えてしまうと、かなり致命的です。数学は暗記じゃない!とは言われますが、こればかりは仕方ない、暗記するつもりで学習してもよいでしょう。
3.2 数学のスタイル
実際に講義を受けたり、参考書を見たりすると、数学の議論は、定義→命題/定理→証明→定義→命題/定理→証明……といったことを延々と繰り返しています。普通、数学はこのようなスタイルで展開されるということを頭に入れておくとよいでしょう。
1.2 で述べたように、数学用語には必ず定義があります。わからない用語があったら、その用語の定義まで遡りましょう。(遡り過ぎ注意)命題/主張を使うときは、必ず証明が要ります。「自明」と書かれていてもいなくても、行間をきちんと自分で証明できるようになりたいです。(願望)
3.3 ''数学語''は丁寧に扱おう
1.2 で述べたように、数学の議論・展開は、''数学語''と数理論理を用いて行われます。これらを丁寧に扱うことで、より正確に数学の理解ができます。
以下に「一次独立の定義」の例を挙げます。
(悪い例)
$${\bm{a}_1,\cdots ,\bm{a}_n}$$が一次独立であるとは,
$${c_1\bm{a}_1+\cdots +c_n\bm{a}_n=0 \Rightarrow c_1=\cdots = c_n =0}$$
(良い例)
$${V}$$を体$${\mathbb{K}}$$上ベクトル空間とする.
$${\bm{a}_1,\cdots ,\bm{a}_n \in V}$$が一次独立であるとは,$${{}^{\forall}c_1,\cdots ,c_n \in \mathbb{K}}$$について,
$${c_1\bm{a}_1+\cdots +c_n\bm{a}_n=\bm{0} \Rightarrow c_1=\cdots = c_n =0}$$
このように、定義や定理で使う文字は、予め何を示すか断っておく必要があります。集合の元であれば、属する集合を、関数であれば、定義域と値域、元の移る先を示す習慣をつけておきましょう。そうすれば、文字が大量になったとき、その文字が、集合なのか実数なのか関数なのか、自分の中で分かりやすくなります。
また、数学では、高校数学以上に文字がたくさん出てきます。同じアルファベットでも、字体が異なれば示すものも異なります。例えば、大文字のSでは、黒板文字$${\mathbb{S}}$$、カリグラフィー$${\mathcal{S}}$$、花文字$${\mathscr{S}}$$、ドイツ文字$${\mathfrak{S}}$$などがあります。そのため、普段から文字を書くときは、丁寧に分かりやすく書くことを心がけましょう。
3.4 証明のコツ(数理論理)
数学の本命といえば定理の証明だと思います。ここでは、大学数学の証明について、いくつかコツを書いておきます。
数学の命題(定理)は、基本的に「仮定」→「主張」の形になっています。例えば、
・$${G}$$:有限群, $${p}$$:素数とする. このとき, $${|G|=p^2 \Rightarrow G}$$:アーベル群.
・巡回群の部分群は巡回群である.
・$${G}$$:巡回群, $${H}$$:$${G}$$の部分群とする. このとき,$${H}$$:巡回群.
・$${G}$$:群, $${H}$$:$${G}$$の部分群とする. このとき, $${G}$$:巡回群$${\Rightarrow H}$$:巡回群.
これは先程の定義と同じ感触だと思います。どんな命題でも、とりあえず「仮定」→「主張」の形に書き直してみるといいと思います。(例の下3つが同じことを述べているように)そうすることで、主張を証明するのに必要な前提が整理され、何を用いて示せばいいかはっきりします。
そして、仮定は全て過不足なく用いなければなりません。足りなけば、そもそも主張として成り立ちませんし、逆に多すぎれば、その主張はもっと厳しい条件で成り立つことができます。(強い命題と言ったりします)証明が終わったら、その証明が仮定を満たしているかどうかを確認しましょう。
また、仮定はあくまでも仮定であることを頭に入れておきましょう。「$${P \Rightarrow Q}$$($${P}$$ならば$${Q}$$)」というのは、あくまでも$${P}$$が成り立ったときだけ$${Q}$$も成り立つと言っています。くれぐれも、示したいのは$${Q}$$であることを意識しましょう。
3.5 とにかく例を考える
1.3で述べたように、数学は抽象度が高いです。そのため、具体例を自分で考えて、その主張がどのようなことを示しているのかを理解するということが必要になってきます。$${n=1}$$を考えたり、$${f(x)=x}$$のように簡単な関数を考えたりしましょう。「例示は理解の試金石」です。
3.6 何を学んでいるか意識する
皆さんは、参考書を選ぶとき/勉強するとき、何を意識しますか?個人的には、学習内容の章節のタイトル、定義や定理の要点を意識することが重要だと思います。それをすることで、これから何をどのような流れで学ぶのかということを頭に入れておけば、何をやっているのか明確になり、ダラダラ学習を防いだりできます。
3.7 諦めない心+数強の友人/先輩を作る
講義や参考書で何を言っているのかわからなくても、諦めないでください。数学は思考する忍耐力が必要です。夢中になれば、食べながら、電車で移動しながらだって考えて考えるほど、数学は楽しいですよ。それでもわからなかったら、数強の友人/先輩を作って、積極的に訊きましょう。数学科だからコミュニケーションは苦手……という人も、きっと学科に数人は数強の人がいます。数学科の攻略には人脈づくりも重要です。
3.8 全部を学ぼうとしない
これは、学び始めの人が陥りやすいポイントです。これまで「定義や定理は厳密にやらないといけない」と述べてきました。ならば参考書にある定理や証明を全部丁寧にやって完璧にしてやるぞ!と意気込んでしまいがちです。
しかし、実際にやろうとすると、それでは分量が多すぎるのです。さらに他の数学の分野の勉強、さらにはそれ以外の勉強、日常生活、サークル活動、バイトなどもあり、圧倒的に時間が足りません。
また、仮に全部学習したとします。そこには特殊な例や重要でない命題もあると思います。ですが、2年次、3年次……の学習内容にそれらが大きく関係することは少ないと思われます。すなわち、何が重要な項目であるかを見極め、学習の取捨選択を行ったほうが、効率的で心の余裕もできると思います。全部を吸収しようとしても、時間の限りがあって窮屈になってしまいますので、落ち着いて学習を進めましょう。
3.9 Tips
ここでは、その他アドバイスなどをまとめておきます。
・数学記号は、基本的に先生毎、試験毎になど、そこで使われているものに合わせるようにしましょう。
・数学用語は、一応英単語でも確認しておきましょう。ゼミなどで洋書を読むときに便利です。英単語から性質のイメージが分かることもあります。
・TeX(LaTeX)を使えるようにしておきましょう。TeX(LaTeX)とは、数式組版ソフトで、数式がきれいに書けます。Wordの数学バージョンという認識です。(インストール方法は各自で調べて下さい)
・デジタル上でノートを取ってもいいですが、個人的には紙のノートとペンで数学をするのがおすすめです。(個人の自由ですが)
おわりに
ここまで読んで頂き、本当にありがとうございました。この記事に、僕の書きたいことをすべて詰め込みました。個人的には良い記事が書けたと思っています。改めて、この記事を読んでくれた方が、よりよい大学生活、そして数学ライフを送れることを願っています。
ありがとうございました。それでは。
この記事が参加している募集
この記事が気に入ったらサポートをしてみませんか?
