【レポート】noteにおけるスキ率を重回帰分析の結果から統計学的に解釈してみた！

自己評価：具体的だからレポートにふさわしいテーマ

世界トップクラスのコンサルティング会社であるマッキンゼーなどの超巨大企業は、これからの時代の重要スキルとしてデジタルフルーエンシーを挙げています。

では、なぜ？

これからの時代、デジタルフルーエンシーが重要なスキルなのか？

デジタルフルーエンシーが重要スキルと考えられている理由は、以下の通りです。

①デジタルは、生活や仕事だけでなく人生のすべての場面でデジタル技術が関わるようになっており、これから、ほぼすべての産業にデジタル技術が広がり、社会は再構築されていくと推定できる。（例：DX（デジタルトランスフォーメーション））

②デジタルフルーエンシーが低いと、デジタル製品を使いこなすのが難しくなり、デジタルを使いこなす人と比べて、

・生産性や仕事の効率が下がる

・会社で成果を出しにくくなる

・転職に成功しにくくなる

などの恐れがある。

③スキルの陳腐化を防ぐ必要があり、ひとつの専門スキルだけで生きていくのは難しくなる。

つまり、デジタルフルーエンシーが高いとDXが起こすデジタル化に対応でき、予測できない変化が起きても、新しいテクノロジーに対応できるなどのメリットがあります。

要は、デジタル技術やツール・製品を使いこなすスキルがあれば、短い学習時間で変化に対応できるため、以下に記載した各学びなおしを、適宜または適時、選択して、

・リスキリング（いま持っていない新しいスキルを身につけること。）

・アップスキリング（すでに持っているスキルを改善したり、より強力にすること。）

・クロススキリング（今持っているスキルとは別の分野のスキルを身につけること。）

・アウトスキリング（企業が従業員に対して用意・実施する教育・転職支援プログラム。）

今、自分が一番必要としているスキルを学ぶことで、より高い専門スキルを身に付けることが、生き残るための近道だと思います。

変化が早い時代では、変化に対応できることが大切です。

だからデジタルフルーエンシーが重要なスキルになるのだと言えます。

簡単に言うと、「目的を達成するために、適切なデジタルテクノロジーやツールを選択し、活用する能力」がデジタルフルーエンシー（デジタルの流暢さ）ですが、物は使いようで、多くの人は、エクセルでのデータ分析はなかなか難しいと思っているかもしれません。

しかし、専門の分析ツールを使わなくとも、できることは意外に多いんですよね(^^)/

そこで、既に、ご存じの方も多いと思いますが、エクセルには「分析ツール」という大変便利な機能があって、この「分析ツール」機能は、ヒストグラムの作成から回帰分析まで19種類もの分析を可能にしてくれます。

以下は「分析ツール」機能で行える分析です。

分散分析：一元配置
分散分析：繰り返しのある二元配置
分散分析：繰り返しのない二元配置
相関
共分散
基本統計量
指数平滑
F 検定: 2 標本を使った分散の検定
フーリエ解析
ヒストグラム
移動平均
乱数発生
順位と百分位数
回帰分析
サンプリング
t 検定：一対の標本による平均の検定
t 検定：等分散を仮定した2標本による検定
t 検定：分散が等しくないと仮定した2標本による検定
z 検定：2標本による平均の検定

「分析ツール」とはエクセルのアドインの一つで、クリックや簡単なパラメータの入力のみでデータ分析を可能にしてくれる機能です。

エクセル「分析ツール」が導入できたら、さっそnoteのデータを利用して分析を行ってみたいと思います。

今回の分析では、実務でよく見かける下記の分析手法を用いて８つのケースを分析してみたいと思ったのですが、

【分析ケース一覧】
分析ケース①：基本統計量でnote記事（データ）の全体像をつかむ／使用する分析手法名：基本統計量

分析ケース②：移動平均でnote記事初投稿からビュー・コメント・スキの傾向を把握する／使用する分析手法名：移動平均

分析ケース③：ヒストグラムでビュー当たりのスキの分布を見る／使用する分析手法名：ヒストグラム

分析ケース④：相関分析でビューとスキに関係性がどの程度あるかを調べる／使用する分析手法名：相関

分析ケース⑤：t検定で２つのデータ（ビューとスキ）に差があるのかを調べる／使用する分析手法名：F検定（t検定（分散が等しくないと仮定した2標本による検定））

分析ケース⑥：分散分析で複数データ（ビューとスキとコメント）の各数値に差があるのかを調べる／使用する分析手法名：分散分析（一元配置）

分析ケース⑦：分散分析でビューとスキに関係性があるかどうかを調べる／使用する分析手法名：分散分析（繰り返しのない二元配置）

分析ケース⑧：回帰分析でコメントに最も影響を与えている施策（ビューやスキ）は何かを探る／使用する分析手法名：回帰分析

・
・
・

分析して行くうちに、めんどくさくなってきたので(^^;

すっ飛ばして、分析ケース⑧のみ検証してみました（爆）

以下に記載した「仮説」について重回帰分析の結果から統計学的に解釈してみました(^^)/

仮説：noteにおけるスキ率は不規則である

参考データ：Instagramは「いいね率」に規則性、Twitterは不規則！

さて、マーケティングに関わる仕事をしている方だと、頻繁に見聞きする言葉の一つに「エンゲージメント」があると思います。

ここで、SNSにおけるエンゲージメント率の計算方法を参考にして、noteにおける主要計算式を仮に作ってみました。

前提条件：エンゲージメントとしてカウントされるものは、記事の投稿に対する以下のユーザーのアクションです。

「スキ」

「コメント」

「投稿のシェア」

noteにおける個人的主要計算式（仮）：

①noteにおけるエンゲージメント数（案１）（反応数）＝投稿におけるスキ数＋コメント数（＋投稿のシェア 数）

②noteにおけるエンゲージメント率 （案２）=noteにおけるエンゲージメント数（案１）（反応数） ÷フォロワー数

③noteにおけるエンゲージメント率 （案３）=noteにおけるエンゲージメント数（案１）（反応数） ÷インプレッション数（投稿を見たかもしれない回数≒ビュー数）× 100

④noteにおけるスキ率（案４）＝１投稿あたりのスキ数の平均値（＝スキ数合計÷記事数合計）÷ フォロワー数 × 100

⑤noteにおけるスキ率＝スキ数 ÷ ビュー数 × 100

この計算式の結果と重回帰分析の主要な計算結果から仮設の妥当性について、ざっくり評価してみたいと思います。

今回、分析対象となるのは、２０２２年１２月５時点でのビュー数とスキ数のデータです。

これに下図のような分析ツールを用いて、重回帰分析を行いました。

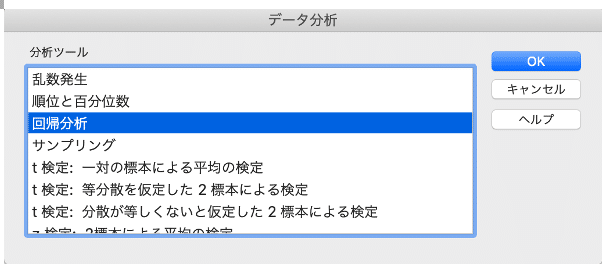
下図のように重回帰分析の結果が出力されます。（色付け＆コメント箇所は、主要な指標を表しています。）

これを用いて推定された回帰式の妥当性や精度を評価してみます。

分析結果の表には様々な指標が表示されており、回帰式の妥当性を正確に評価するためには、各指標の意味を理解する必要がありますが、最も重視したい指標は、以下となります。

・重決定（R2）と補正R2

・有意F

・P値とt 値

■重決定 R2（決定係数または寄与率）

「重決定 R2」は、回帰分析における一般に使われる決定係数のことであり、「寄与率」とも呼ばれています。

この係数は、回帰分析から得られた回帰式が目的変数の値変動をどの程度説明できているかを表す（求められた回帰モデルのデータへの当てはまりの良さを示す）指標でり、0〜1の値を取り、1に近ければ近いほど、データに対する当てはまりが良く、回帰式の精度が高いことを意味しています。

ここで、注意すべき点としては、「重決定 R2」の目安を、どう考えるかなんですが、残念ながら「重決定 R2」がいくつ以上であれば良い、という統計学的基準はありません。

そのため、「重決定 R2」の基準は、回帰分析を行う人が経験的な判断から決めることになります。

ただ、一般的な目安としては0.5や0.6以上あれば、有用な回帰式が得られたという判断をする場合が多いようです。

なお、あくまで目安になるので、解析対象の状況に応じて異なることに注意してください。

ただ、1つの目安として、下記のような基準で行ってみるのが良いと考えます。

但し、この目安も、データサイエンティストに依っては、R2≦0.6だと全く使えないという人もいますので、目安の1つ程度で把握していただければと思います。

R２≧0.8　精度が良い

R２≧0.5　精度がやや良い

R２≧0.2　精度が悪い

その事を理解した上で、前述のデータを確認してみると・・・・・・

げぇ？！

重決定 R2（決定係数または寄与率）が「0.112885187539577」ってことは、「精度が悪い」結果であり、これは推定された回帰式がスキ数の変動の96％を説明できていないことを表すので、良い精度の回帰式が得られていないことを意味していますねぇ(^^;

解析終了！

よって、「noteにおけるスキ率は不規則である」という仮説は、私のデータの分析結果から解釈すると、正しいと「推定」（ある事実を手掛かりにして、物事を推し量り仮に判断すること。）だと言えそうです。

それじゃ、検証おしまい（爆）

えっ？

おい！

早すぎだろう結論だすの(^^)

そう、結論を出すのは、この時点では、早計です(^^;

「推定」と表現したのには理由があって、データの分析及び検証を重回帰分析で行う場合、失敗しないために、以下に示す組み合わせ・構造・データの問題について予め確認しておく必要があります。

・組み合わせの問題：「要素が少なすぎる」「要素が多すぎる」「強い相関がある（多重共線性）」「成果が絞れていない」

・構造的な問題：「見せかけの相関」「複数のつながりの構造が混ざっている」「時間差がありすぎる」「特殊な要因が影響している」

・データの問題：「成果をデータにできない」「データの精度が低い」

出て来た結果に対して、 直感的に「何が起きているのか」をとらえ、より早く正しく「どう対処すればよいのか」を判断できるようになるためにも、経験を積まないと、ね(^^)/

つまり、分析は、「仮説」と「解釈」次第で変わってきます。

分析手法そのものは論理的に、数学的な根拠を持って確立しているものですが、それをどのように用いるのか？

また、その結果をどのように現実に当てはめるのか？と、分析者に委ねられる部分が非常に多くあるのだという事実があります。

質の良い分析を行うためには、分析者の洞察力に根ざした質の良い「仮説」と、得られた結果に対する多面的な「解釈」のどちらもが必要になるので、何かを検証する場合は、その点に注意してみてください。

今回の様に、分析者が私ひとりの場合は、偏りが発生する・視野が狭くなってしまう・・・・・・ということも発生しがちです(^^;

そのため、可能であれば、ひとりで分析をせずに、チームで協力して分析を行うことをオススメします。

さまざまな視点で考えることで、仮説の設定や分析の読み取り（解釈）がより精度高く行えると考えます。

以上の解析結果（精度が悪い）や分析する上での心構えを踏まえた上で、ひと通り、解析結果を簡潔に確認してみますね(^^)/

■補正R2（自由度調整済み決定係数）

「補正R2」は、実は、重回帰分析で一番重視される指標です。

重決定R2は、説明変数の個数が多くなればなるほど1に近づく性質があるため、重回帰分析の回帰式の精度を評価する上で限界があるため、普通の決定係数がデータ数の増加とともに無条件に上昇してしまうことを補正する役割を果たす補正R2で確認しておく必要があります。

複数の説明変数を使って行う重回帰分析の場合は、説明変数の個数の影響を取り除いた「補正R2」の値を確認する必要があるのですが、今回のデータの変数は「スキ」のみなので、「補正R2」の手番は無しでOKです。

■有意F

有意Fは「回帰分析に使用した説明変数の組み合わせに意味はない」という確率を表すものでり、この数値が小さければ小さいほど、「偶然の可能性が低い」=「意味のある回帰式を得られた」と解釈することができます。

あくまでも目安としてですが、有意Fが0.05または0.01未満であれば、有用な回帰式を得られた可能性が大きいと判断できます。

その事を理解した上で、前述のデータを確認してみると・・・・・・

お！

有意Fが「6.35708E-26」ってことは、「偶然の可能性が低い」=「意味のある回帰式を得られた」と解釈できるってことだね。

■t値

t値はP値と同様に、それぞれの説明変数が目的変数に与える影響の大きさを表す指標です。

目安として、t値の絶対値が大きければ大きいほど、目的変数に与える影響が強いことを意味しています。

逆に、t値の絶対値が2より小さい場合は、統計的に判断してその説明変数は目的変数に影響を与えていないと判断します。

その事を理解した上で、前述のデータを確認してみると・・・・・・

おお！

P値が「10.8551057157216」ってことは、「目的変数に与える影響が強い」と解釈できるってことだね。

なお、P値が小さければ小さいほどt値は大きくなるので、時間がない場合、P値の方のみ観察するのもよいと考えます。

■P値の確認と回帰式の評価

まず、Pについて確認しておくと、「probability(確率)」の頭文字からとってきていて、個別の説明変数の1つ1つが目的変数に対して関係があるかどうかを表す指標です。

分析ツールのデフォルトの信頼度設定は95%となっているため、信頼水準はデフォルトの95%を使っていると仮定すると、P値を100%-95%=5%（0.05）と比べて、算出された係数を使えるかどうかを判断します。

一般的に、P値が0.05未満であれば、その説明変数は目的変数に対して「関係性がありそう」という判断をし、0.05以上の場合は「関係がなさそう」と捉えることができることから、P値が0.05未満であれば、その説明変数は目的変数に対して「関係性がありそう」と言えるので、分析に使えそうだと判断できます。

それでは、実際に今回の分析結果において、肝心なP値を観察し、「スキ」の説明変数が目的変数に対して関係があるかどうか？を確認してみますね。

その事を理解した上で、前述のデータを確認してみると・・・・・・

P値が「6.35708E-26」ってことは、回帰式の評価精度は低いけど、P値が評価可能であり、かつ0.05を下回る（あるいはt値の絶対値が2を超える）説明変数：スキ数は、何かと「関係性がありそう」と推測できそうですね。

この分析における次のアクションとしては、説明変数を再選択（例えば、文字数とかコメント数等。）した上で、重回帰分析を再度実施し、上記と同じように、その結果を評価することです。

これはExcelを用いた分析や回帰分析に限ったプロセスではなくて、どんなデータ分析でも、データの理解（前述の組み合わせ・構造・データの問題に注意）、データの前加工、初期分析、評価、試行錯誤の繰り返しが続きます。

今回は、エクセルの分析ツールによって出力された結果の妥当性を解釈することにフォーカスをあてました。

今の時代の要請もあり、ビジネスにとって、スピード感がある解析手法を屈指するのも良いのですが、私たちは、「人間だもの（笑）」、統計学的な理解を見逃しやすいのは事実であり、その結果、失敗することもありますから^^;

注意しながら解析してみてください、ね(^^)

■所感
Excelで分析を行う利点の１つは、自動出力される豊富な統計学の指標に意識が集まることにありますので、良かったら、みなさんも、身近な物を対象にして、基本に立ち返ってExcelの分析をやるとリフレッシュできるし、思いもよらない面白い解析結果が得られるかもしれませんよ（ニヤリ）

■参考資料
参考までに、最新集計時刻 2022年12月13日 09:36時点でのnoteにおける個人的主要計算式（仮）の計算結果は、以下の通りです。

①noteにおけるエンゲージメント数（案１）（反応数）＝投稿におけるスキ数+コメント数（＋投稿のシェア 数）＝28,490

②noteにおけるエンゲージメント率 （案２）=noteにおけるエンゲージメント数（案１）（反応数） ÷フォロワー数≒28.376%

③noteにおけるエンゲージメント率 （案３）=noteにおけるエンゲージメント数（案１）（反応数） ÷インプレッション数（投稿を見たかもしれない回数≒ビュー数）× 100 ≒7.21%

④noteにおけるスキ率（案４）＝１投稿あたりのスキ数の平均値 ÷ フォロワー数 × 100 ≒2.74%

⑤noteにおけるスキ率＝スキ数 ÷ ビュー数 × 100 ≒7.16%

【参考記事】
「重回帰分析」を理解してもらうために全力で頑張ってみた！【やさしい統計学15】
https://yasabi.co.jp/重回帰分析/

Instagramは「いいね率」に規則性、Twitterは不規則！8,000～30,000フォロワーを持つインスタグラマーが超優良！
https://prtimes.jp/main/html/rd/p/000000035.000011944.html

noteはいいね獲得率（いいね数÷PV数）10%UPを目指すと良い感じになると思う
https://note.com/ng2014/n/nf800b6f6eb1a

noteのビュー数とスキ数の指標スキ率をポップアップが届いたついでに考えてみた！
https://note.com/yarapon2/n/ne9344f9cc87e

noteのビューとスキの割合で計算した「スキ率」を分析しても記事の需要や評価はわかりません
https://note.com/shichaoji/n/n7c693af506b8

エンゲージメント率の定義とは？SNSごとの計算方法やエンゲージメント率を高める方法
https://www.tsuhannews.jp/shopblogs/detail/68529

コラムとは？分かりやすくて面白いコラムの書き方・構成のコツを紹介
https://www.siteengine.co.jp/blog/column/

有名心理学的効果を使った、思わず読みたくなる記事の作り方まとめ
https://liginc.co.jp/web/useful/97591

タイトルに70％の労力を　記事タイトルの効果的な付け方
https://www.innovation.co.jp/urumo/article_title/

Webライター必見！「読まれる記事」の書き方と注意点
https://mynavi-creator.jp/blog/article/how-to-write-for-web-writer