
関連を検討するときの考え方のコツ
学生の研究の指導をしていてまずつまづくのが,自分が考えていることをなかなか心理学の研究に乗せることができない,という点です。
自由にあれこれと考えていることをそのまま研究に結びつけることができれば良いのですが,それを指導教員に言うとたいてい,「それは無理。研究にできない」という返事が返ってきてへこんでしまったりします。
何が足りないのかというと,基本的な,「検証可能な」仮説の立て方だと思うのです。今回はそういう話をしてみようと思います。
関連がある
いちばんシンプルな仮説は,「何かと何かに関連がある」というものです。
たとえば,下の図(散布図)のような状態が関連です。横軸を動機づけの得点,縦軸を学力テストの得点としましょう。1つ1つの○は,調査対象者です。するとこの図は,動機づけが高い人(横軸が右方向に行く人)ほど,学力テストの点が高い(縦軸が上方向に行く)ことを表します。
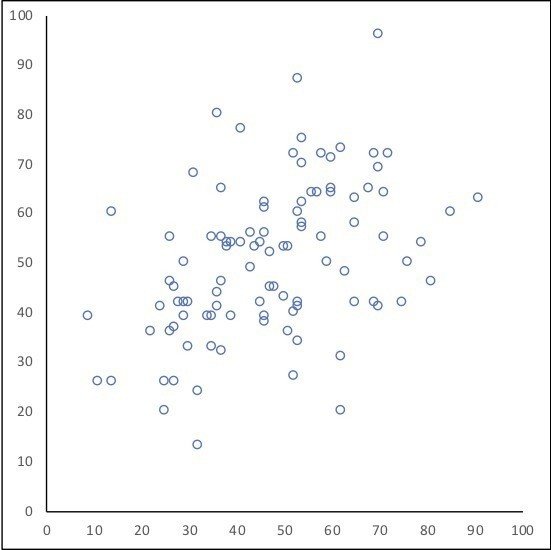
もしも「動機づけが高い生徒ほど,試験の成績が良い」という仮説を立てて,この結果が得られたのであれば,「仮説は検証された」ということになるわけです。
ふたつの群
どちらよりもどちらの方が平均的に高い・低い、ということを問題にすることがあります。
「背の低い人よりも,背の高い人の方が体重が重いだろう」とか,「女性よりも男性の方が背が高いだろう」といった問題です。
先ほどの関連の図で,横軸を中央で区切ります。そして,高い群と低い群を作ります。そのふたつの群で縦軸の平均値を比較します。
この状態が,「〇〇が低い人たちよりも高い人たちの方が,△△が高い」という関係を表しています。
これも「関連」です。表現の仕方は「こっちの方がこっちよりも高い・低い」なのですが,図を見てわかるように,片方の軸をカテゴリにしただけと考えることができるからです。
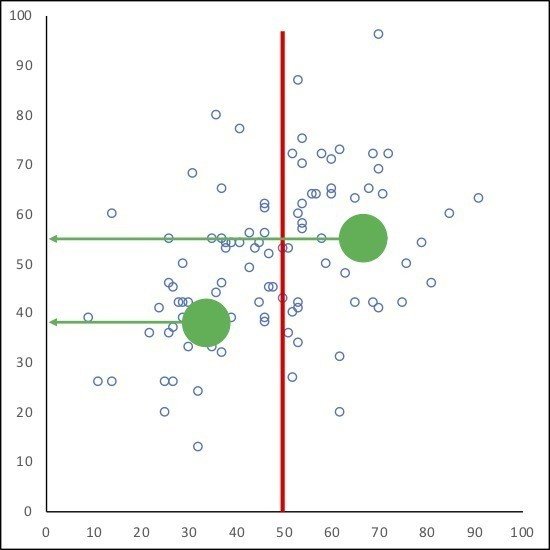
低い・高い,という問題も関連だという見方ができると,少しだけ仮説を立てやすくなるように思います。
ここで横軸を3段階に分類すると,「次第に上がって・下がっていく」というだけでなく,「あるグループだけ高い・低い」といった関係を検討することができるようになります。U字型や逆U字型の関係や,端だけ高く・低くなるような関係です。
多いか少ないか
さらに,縦軸も平均値で高い・低いに分けてみましょう。
この図式は「○○と××の組み合わせの人が多い(少ない)」という仮説に相当します。
「背が高く体重が重い人たちは,背が高く体重が軽い人たちよりも多い」とか「男性で背が高い人たちは,女性で背が高い人たちよりも多い」といった仮説です。
「人数の多さ・少なさ」を問題にしていますので,関連のようには思えないかもしれません。しかしこの図を見て分かるように,これも「関連」なのです。
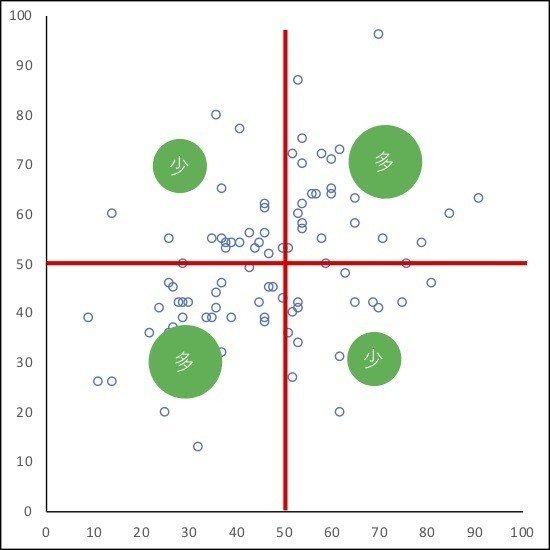
関連の言い換え
たまに,すでに関連を示しているにもかかわらず,「それで,この得点が高い人の方が平均値が高いのですか?」と尋ねてくる人がいるのです。しかし,ここで示した3つの図を見れば分かる通り,いずれも関連です。
◎Aが高く(低く)なるほどBも高く(低く)なる
=Aが高い人は低い人よりもBの平均値が高い(低い)
=AもBも高い人は,Aが高くBが低い人よりも多い(少ない)(ただし他の組み合わせもありますが)
こういった言い換えができると良いと思います。
問題は関連の大きさ
「Aが高い人と低い人を比べると,Bの平均値に違いが見られる」は「AとBとの間に関連がある」と同じことを示しているという話でした。
ここでの問題は,「どれくらいの関連があるか」ということです。「どれくらい違いがあるか」でも構いません。この関連や違いの程度を,効果量という数値で表します。一般的な相関係数は効果量ですし,平均値の差であれば d や h やgといった記号で表されます。関連や差が「ある」「ない」だけではなく,これらの大きさを問題にしましょう。
面白い関連
もしも卒論などで関連や差を問題にするのであれば,「面白い関連」を探すのがよいでしょう。それは簡単な問題ではありません。
「外向性と社交性に関連があるかどうかを検討します」と言われれば,「関連があって当たり前でしょう」という答えになります。「男女で身長の平均値に差があるかどうかを検討します」と言うのも同じです。それも「差があって当たり前」です。
それから,面白そうな関連については,たいていすでに研究が行われています。それはそうですよね。誰もが思いつきそうな「面白そうな関連」であれば,当然研究者はそこに目をつけていると考えられるからです。
誰も気づいていないような関連を探そうとすると,重箱の隅をつつくようなとても小さな関連を探す方向に行くかもしれません。でもそのような小さな関連を検証するのは簡単ではありません。小さな関連は大きなサンプルでより確実に確認されます。偶然関連が生じたのではない,ということを言うのも簡単ではありません。
まだ誰にも気づかれていない,「ここにこんな関連があったのか!」という研究ができると理想的です。ぜひ,探してみてください。
ここから先は

日々是好日・心理学ノート
【最初の月は無料です】毎日更新予定の有料記事を全て読むことができます。このマガジン購入者を対象に順次,過去の有料記事を読むことができるよう…
この記事が気に入ったらサポートをしてみませんか?
