
チューリング理論で解く『魚の模様』の秘密
こんにちは、ANGLERSのエンジニアのリッキーです。今回は、魚の模様の秘密に迫り、数学とシミュレーションを使ってその謎を解明していきます。
私がこのテーマに興味を持ったのは、日々、ANGLERSユーザーのみなさんから寄せられる釣果データの中で、魚の模様が持つ美しさと不思議さに心を惹かれたからです。

このブログを通して、魚の模様の背後にある科学的なメカニズムを知ることで、釣りや魚に対する興味をさらに深めていただければ幸いです。
また、エンジニアとして特に感銘を受けたのは、これらの模様がコンピュータの父と称されるアラン・チューリングの理論に基づいていると知ったことです。チューリングが計算理論だけでなく、生物学にも深い洞察を持っていたことに驚きました。
それでは、さっそく魚の模様の探求を始めましょう。
魚の模様の美しさとその秘密
魚の模様は、まるで自然が描いたアートのような美しさを持っています。例えば、鯖の青と銀の縞模様や、イワナの斑点模様など、見る者を魅了する多様なパターンがあります。


魚の模様が生態系や魚の行動にどのような影響を与えるかについても、興味深い点が多くあります。例えば、メバル属の黒い斑点模様はカモフラージュの役割を果たし、岩場や海藻の中で捕食者から身を守るのに役立ちます。

一方で、イシダイの縞模様は非常に目を引くものですが、その模様の具体的な機能や理由はまだ完全には解明されていません。こうした未解明の模様も多く、魚の模様の研究にはまだ数多くの謎が残されています。

一見すると魚の模様はDNAによって決まると考えがちです。実際、私自身もこのテーマを調べるまではそう思っていました。確かに、遺伝子は模様の基礎を提供しますが、実際にはそれ以上に興味深いメカニズムが関与しています。
模様の形成には、「反応拡散系」と呼ばれる数学的なモデルが重要な役割を果たしています。このモデルでは、一見複雑な模様を、シンプルなルールの組み合わせによって説明することができます。それでは、これについて詳しく見ていきましょう。
模様形成の仕組み
「波」によって数学的に決まる模様
魚の模様がどのようにして形成されるのか、その答えは「波」にあります。ただ、魚をテーマにした話の中で「波」と聞くと、海の波を連想しがちですが、ここで言う「波」とは、物理的な波ではなく、数学的なモデルで生じる現象を指しています。
反応拡散系と呼ばれる数学モデルは、化学物質がどのように空間内で反応し、拡散するかを説明するモデルです。このモデルでは、二つの物質が互いに反応し、一方が他方を抑制しながら、一定のパターンを作り出すことができます。
この現象は「波」のように見えることから、数学的な波と呼ばれています。
反応拡散モデルの基本概念は、二つの主要な要素に基づいています。一つは活性因子(アクティベーター / Activator)であり、もう一つは抑制因子(インヒビター / Inhibitor)です。
活性因子は自己増殖する性質を持ち、抑制因子は活性因子の増殖を抑制する役割を果たします。この二つの物質が互いに反応し合いながら、空間内で拡散することで、特定の模様が形成されます。
例えば、鯖の青と銀の縞模様やトラウトの斑点模様も、この反応拡散モデルの結果として生じます。特定の化学物質が細胞内で生成され、それが周囲に拡散する過程で、模様が形作られます。
アラン・チューリングの理論
この反応拡散モデルを最初に提唱したのは、アラン・チューリングです。チューリングは1952年に「The Chemical Basis of Morphogenesis(形態形成の化学的原理)」という論文で、この理論を提唱しました。
彼の理論は、自然界に見られる様々なパターン(例えば、シマウマの縞模様やヒョウの斑点模様)が化学物質の反応と拡散によって説明できることを示しています。
<チューリングについて>
少し脱線しますが、アラン・チューリングは、コンピュータ科学の基礎を築いた人物として知られています。彼は、1936年の論文で抽象的な計算モデルであるチューリングマシンを提唱しました。これが現代のコンピュータの基本的な設計思想の基礎となりました。
また、第二次世界大戦中には、ナチス・ドイツのエニグマ暗号を解読するための機械を開発し、連合国の勝利に貢献しました。(この時のチューリングの活躍は、映画「イミテーション・ゲーム」でも描かれています)
さて、本題に戻ると、チューリングの理論は、二つの物質がどのように反応し拡散するかを以下のような数式で表現します。
$$
\frac{\partial u}{\partial t} = D_u \nabla^2 u + f(u, v)
$$
$$
\frac{\partial v}{\partial t} = D_v \nabla^2 v + g(u, v)
$$
ここで、$${u}$$は活性因子、$${v}$$は抑制因子、$${D_u}$$と $${D_v}$$はそれぞれの拡散係数、$${f}$$と$${g}$$ は反応の非線形項を表しています。この方程式は、二つの異なる化学物質が時間とともにどのように変化し、空間内でどのように分布するかを示しています。
近距離の排除効果と遠距離の生存効果
チューリングの理論は、二つの基本的なロジック、「近距離の排除効果」と「遠距離の生存効果」に基づいています。
近距離の排除効果: 活性因子が自己増殖する性質を持ち、近距離で急速に増殖しますが、抑制因子の存在によってその増殖が抑制されます。これにより、近くの領域での過剰な活性因子の増殖が防がれます。
遠距離の生存効果: 抑制因子は活性因子の増殖を抑制する一方で、遠距離に拡散して影響を及ぼします。このため、遠距離では活性因子の増殖が抑制されず、特定のパターンが形成されます。
このように、活性因子と抑制因子のせめぎ合いが化学反応の「波」を生み出し、それが動物の模様を作るというのがチューリングが発表した仮説でした。
近藤滋教授による証明
上述のように、1952年にアラン・チューリングは、二つの仮想的な化学物質が特定の条件下で互いの増殖や抑制をコントロールし合うことで、空間にパターン(波)を作り出すことを数学的に証明しました。
これにより、シマウマの縞模様やキリンの網目模様などが生成される理論が生まれました。しかし、当時のコンピュータ技術の限界や生物学者の関心の薄さから、この理論は長い間、証明されずにいました。
その後、1970年代にコンピュータ技術の発展もあり、シミュレーションによってチューリングの理論が再評価され、さまざまな動物の模様がシミュレートされ実際に模様を再現することが出来ました。
しかし、結局それだけでは「動物の模様が反応拡散波である」という証明にはならず、この理論はその後さらに20年以上もの間、確定的な証拠がないまま放置されていました。
時を経て、チューリングの理論を実際に証明したのは、日本の近藤滋(Shigeru Kondo)教授でした。近藤教授は、スイス留学中にチューリングの理論と出会い、その理論を証明するために多くの動物を観察しました。最終的に、タテジマキンチャクダイの縞模様が成長に伴い変化することを発見し、これがチューリングの反応拡散モデルと一致することを示しました。
タテジマキンチャクダイの生きた反応拡散波を発見したことにより、いままで理論でしかなかったものを、実験による検証可能とした近藤教授のこの研究「A reaction–diffusion wave on the skin of the marine angelfish Pomacanthus」は大変好評を博し、科学誌「Nature」の表紙を飾りました 。
その後も、近藤教授はこの分野のパイオニアとして、研究を通じて動物の模様形成のメカニズムを次々に解明しています。(私自身も、このブログを書くにあたって近藤教授の著書を読み、多くを学びました)
下記は近藤教授の研究室(大阪大学大学院生命機能研究科 パターン形成研究室)のHPですのでぜひご覧ください。
オセロを用いた模様形成シミュレーション
さて、ここまで魚の模様を形成する仕組みについて解説してきましたが、ここからは実践編として、実際に手を動かして確かめてみましょう。今回は、オセロを使った実験を行います。
チューリングの理論を理解するには、オセロが非常に効果的です。「動物の色素細胞」を「オセロの石」に置き換えて考えることで、盤面上で白と黒の石が領域を取り合うように、2つの色素細胞(活性因子と抑制因子)が表皮上で領域を取り合う結果、模様が生まれるというイメージです。
なお、このオセロを使った再現アイデアは、上述の近藤教授の著書から参考にさせていただきました。
オセロのルール
チューリングの理論を再現するために、以下の2つのルールを使ってオセロをプレイします。
ルール1: 近距離の排除効果
隣接するマスにある他の色の石によって石がひっくり返される、通常のオセロのルールです。例えば、黒の石が白の石に囲まれると、黒の石が白にひっくり返されます。今回は「周囲4つ以上を敵の色に囲まれた場合、その石は反転する」というルールを適用します。
ルール2: 遠距離の生存効果
チューリング理論の「遠距離の生存効果」を再現するため、特別ルールを追加します。具体的には「2マス以内がすべて自分と同じ色だった場合、その石は反転する」というルールです。これにより、近距離では抑制されるものの、ある程度の距離がある場合は模様が維持される効果を再現します。
Step1. 「オセロ石」の初期配置
それでは実際にオセロを始めていきます。今回はGoogle Spreadsheetを使用して、縦横30マス、合計900マスの領域を用意し、手動でシミュレーションを行いました。まず、この900個のマスにランダムに石を配置します。SpreadsheetのRAND関数を使い、0と1を振り分け、条件付き書式機能で、0を青色、1をグレーに色付けしました。

Step 2. 「ルール①:近距離の排除効果」の適用
次に、ランダムに配置された石に対して「周りを4つ以上、敵の色に囲まれた場合、その石は反転する」というルール①を適用します。下図では、影響を受けた部分が分かりやすいように、青からグレーに反転したものを薄いグレー(数字は2)、グレーから青に反転したものを薄いブルー(数字は-1)で表しています。

Step 3. 「ルール②:遠距離の生存効果」の適用
続いて、ルール②「2マス以内がすべて自分と同じ色だった場合、その石は反転する」を適用します。ルール①と同様に、影響を受けた部分を薄いグレー(数字は2)と薄いブルー(数字は-1)で表しています。
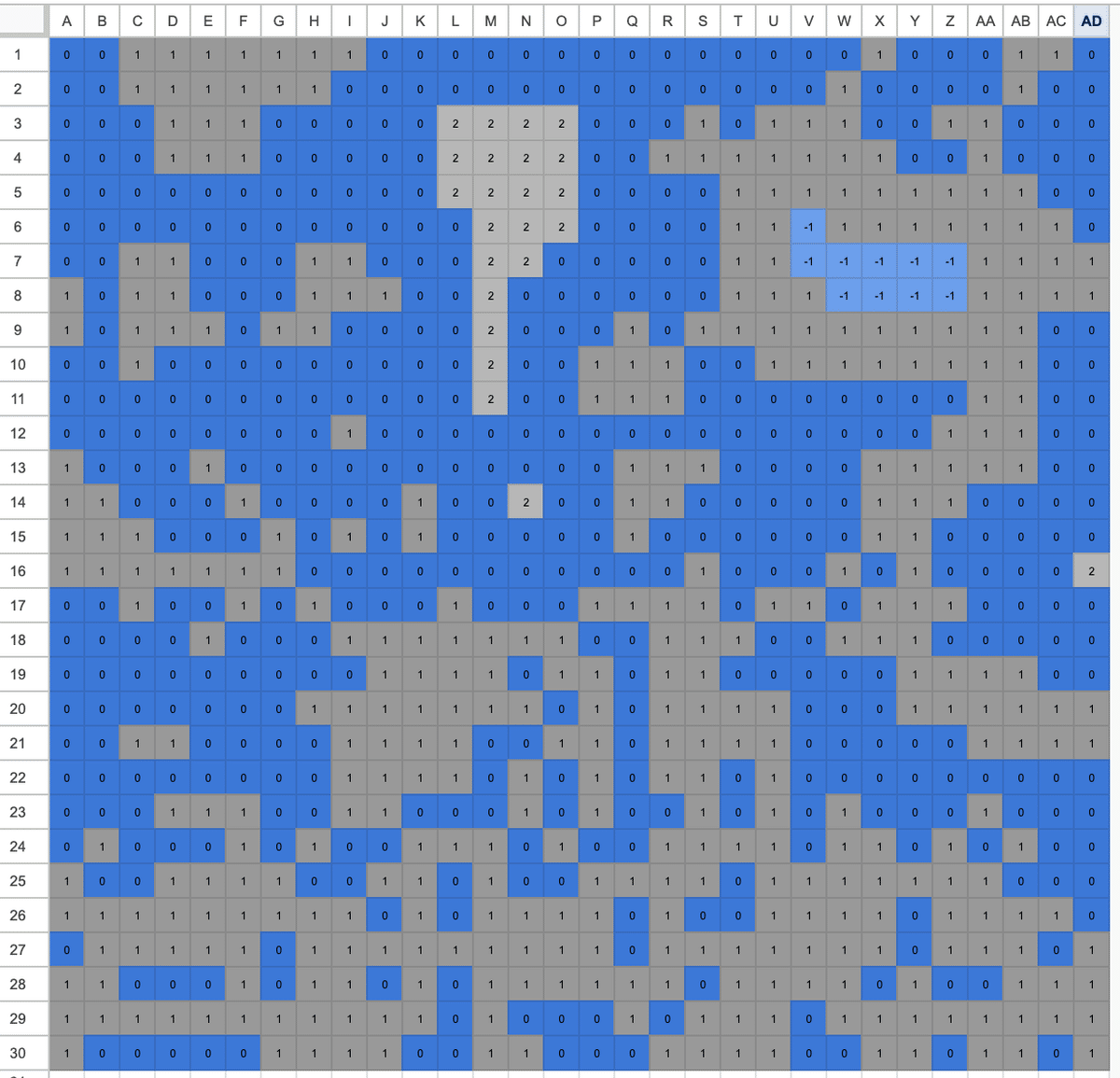
上図からも分かるように、ここまでで既に初期状態と比較すると、模様らしき状態が形成されていることがわかります。
Step 4. 「ルール①、②」の適用を繰り返す
次に、Step2~3で行ったルール①およびルール②の適用を繰り返します。
2周目のルール適用の結果

3周目のルール適用の結果

初期状態から3ループ目までの変化をまとめた図は以下の通りです。

図からも分かるように、今回のような単純なルールを3回適用するだけで、動物(蛇のような模様)に似たパターンが生成できることが確認できました。
このように、数式で見ると一見難解に思える理論も、手動の実験で再現できるほどシンプルな原理に基づいていることがわかります。
コンピュータによるシミュレーション
前章では、手動のシミュレーションでチューリング理論の概要を掴みました。次に、コンピュータを用いて、より本格的なシミュレーションに挑戦します。今回は、代表的なチューリングパターンである鯖の模様形成をシミュレートしてみます。
Gray-Scottモデル
今回のシミュレーションでは、Gray-Scottモデルという数理モデルを使用します。Gray-Scottモデルは、反応拡散系の一種で、以下のような反応のルールに基づいて計算が行われます。
活性因子は、自己増殖する性質を持ち、特定の速度で増殖しようとします。
抑制因子は、活性因子の増殖を抑制し、その濃度を減少させる役割を果たします。
拡散項は、両方の因子が空間内で広がるプロセスを示し、活性因子は遅い速度で、抑制因子は速い速度で拡散します。
反応項は、活性因子と抑制因子の間の相互作用を示し、活性因子が抑制因子によって消費され、抑制因子が活性因子によって生成されます。
供給項は、外部から活性因子が供給される速度を示し、システム内の全体的なバランスを保ちます。
Gray-Scottモデルの方程式は以下のようになります。それぞれの式において、左から、拡散項、反応項、供給項になっています。
$$
\frac{\partial u}{\partial t} = D_u \nabla^2 u - uv^2 + F(1 - u)
$$
$$
\frac{\partial v}{\partial t} = D_v \nabla^2 v + uv^2 - (F + k)v
$$
$${u}$$:活性因子の数
$${v}$$:抑制因子の数
$${D_u}$$:活性因子の拡散係数
$${D_u}$$:抑制因子の拡散係数
$${\nabla^2 u}$$:活性因子のラプラシアンフィルタ
$${\nabla^2 v}$$:抑制因子のラプラシアンフィルタ
$${F}$$:活性因子の増殖係数
$${k}$$:抑制因子の減少係数
ラプラシアンフィルタ
上記の方程式に含まれるラプラシアンフィルタ($${\nabla^2 u}$$ や$${\nabla^2 v}$$)は、画像処理やシミュレーションにおいてエッジ検出や空間的な変化を強調するための手法です。
ラプラシアンフィルタは、周囲のピクセルの値を用いて中心ピクセルの値の変化を計算します。これにより、今回の場合は、化学物質の拡散を数値的にシミュレートすることが可能になります。
具体的には、各ピクセルの周囲のピクセルとの差を計算し、その結果を新しい値として設定します。この操作により、画像のエッジ部分が強調されると同時に、シミュレーションにおいて化学物質の濃度変化が表現されます。
2次元の場合、ラプラシアンフィルタは次のように表現されます。
$$
\nabla^2 u = \frac{\partial^2 u}{\partial x^2} + \frac{\partial^2 u}{\partial y^2}
$$
ラプラシアンフィルタは、Gray-Scottモデルのシミュレーションにおいて、拡散を効率的に計算するための手段となっています。
Houdiniによる実装
シミュレーションツールとして、今回はHoudiniという3DCGソフトを使います。
Houdini上での実装をブログ形式で詳細に解説するのは難しいため、ここでは主なポイントだけを紹介します。
Houdiniのblurノードを利用して、ラプラシアンフィルタに相当する効果を計算
HoudiniのSolverノードを利用して、タイムステップごとに反応拡散方程式を計算
まず、球体上にチューリング模様を生成するシミュレーションを行いました。Houdiniで実装したノードエディターの画面は以下の通りです。


シミュレーション結果
球体上にチューリング模様を生成したシミュレーション結果は、以下の動画のようになりました。
次に、球体ではなく、鯖を意識した魚の形状を持つオブジェクトに対して、同様のチューリング模様をシミュレートしました。
動画からも分かるように、理論に基づいた実装を行うことで、3DCG上でもチューリング模様を生成することができました。(ただし、私のCGスキルはまだ未熟でリアリティに欠ける部分があるため、今後は関連スキルを身につけて、リアルな魚体のCG生成にも取り組んでいきたいと思います。)
まとめ
今回は、魚の模様の形成に関する理論やシミュレーションについて探求しました。魚を含む動物の模様は、アラン・チューリングが1952年に発表した仮説により、数学的に説明可能となりました。
この仮説は、コンピュータの父とされるチューリングが生物学分野で執筆した唯一の論文であり、彼の天才ぶりと今回のテーマの神秘さを改めて感じさせます。
チューリングの「動物の模様は”波”によってできる」という仮説(反応拡散理論)は、その後、日本の近藤滋教授によって実証され、模様形成の研究に大きなブレイクスルーをもたらしました。
実践編ではチューリング理論を理解するために、オセロを使った手動のシミュレーションを行い、初期のランダムな状態から徐々に模様が生成される過程を観察しました。
また、Gray-Scottモデルを用いて、コンピュータ上で鯖の模様をシミュレートし、数学的理論によって自然界の美しいパターンを再現できることを確認しました。
今回の探求を通じて、私は魚の模様をただの美しさとしてだけでなく、その科学的背景を理解して楽しめるようになりました。読者のみなさんも、このブログを通じて少しでもその魅力を感じ取っていただけたら嬉しいです。
最後までお読みいただき、ありがとうございました。
一緒にはたらく仲間を積極採用中!!
アングラーズは現在、エンジニアやCS、コーポレートMGRなどさまざまなポジションを積極的に募集しています。リモートでのコミュニケーションが多い当社ですが、年4回(*うち2回オンライン)の決起会を通じて一体感を高めています。
⚫️ 釣りに、仕事に、熱量の高いメンバーと、当事者意識を持って仕事がしたい!
⚫️ 社会へのインパクトが大きい仕事に携わって、経験値を上げたい!
⚫️ まだ誰も見たことがないサービスを世の中につくりたい!
など、釣りや趣味領域での事業に興味のある方はぜひ、私たちと一緒に釣り業界を盛り上げましょう!
少しでも気になった方は、以下よりエントリーをお待ちしております!
その他、採用情報はこちらからご覧いただけます!
ご興味のある方はぜひお気軽にエントリーください。

参考文献:
https://www.dna.caltech.edu/courses/cs191/paperscs191/turing.pdf
https://www.fbs.osaka-u.ac.jp/labs/skondo/ozaki/what%20is%20RD%201%20by%20ozaki.htm
frankfurt.de/~gros/StudentProjects/Projects_2020/projekt_schulz_kaefer/
https://www.brh.co.jp/publication/journal/011/to_1
https://www.amazon.co.jp/dp/4044004595
https://www.amazon.co.jp/dp/4054067611
https://www.amazon.co.jp/dp/4802511027
https://ja.wikipedia.org/wiki/反応拡散系
https://ja.wikipedia.org/wiki/アラン・チューリング
この記事が気に入ったらサポートをしてみませんか?
