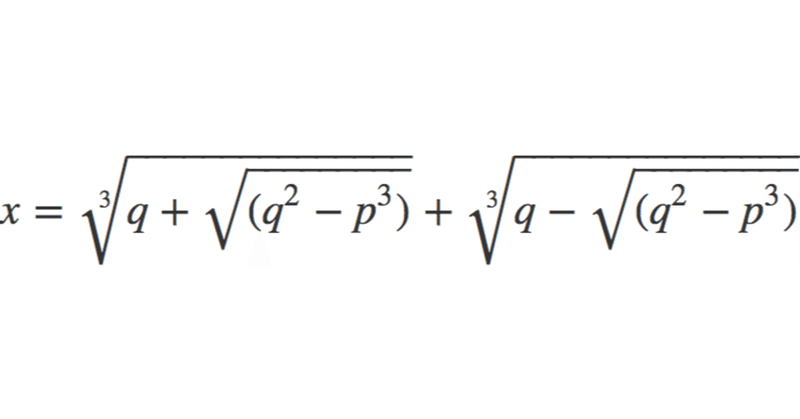
20010501　複素数(2)

　複素数$${^{*1}}$$の続き。複素数$${^{*2}}$$は$${x^2+1=0}$$のように実数解を持たない方程式にも解を持たせたい、というところから導入されたのではないらしい。

　三次方程式の解を求める公式を探っている中で、その実数解を表現するための公式の中に負数の平方根を用いなければならないところが出てきた。このように、普通に考えると矛盾して不都合に思える状況から複素数が生まれてきたようだ。

　三次元方程式の一つの解を表す公式としてカルダーノの公式$${^{*3}}$$がある。

$${x^3-3px-2q=0}$$　の時

ある実数解の一つは次の式によって表される。

$${x= \sqrt[3]{q+\sqrt{(q^2-p^3)}}+ \sqrt[3]{q-\sqrt{(q^2-p^3)}}}$$

　実数解を表しているのだが、$${q^2-p^3}$$が「負」になった場合はどうなるだろうか。

　例えば次の三次方程式の解を考える。

$${x^3-4x+3=0}$$ の場合、

$${p=4/3}$$、$${q=-3/2}$$ で $${q^2-p^3= {-13}/{108}}$$

となり根号の中が「負」になる。

　ところが$${x^3-4x+3=(x-1)(x^2+x-3)}$$なので解の一つは「$${1}$$」である。あと二つの解は$${x^2+x-3=0}$$を解けばよい。二次方程式の公式から

$${x=(-1±\sqrt{13})/2}$$

となり上記の三次方程式の三つの解はすべて実数である。カルダーノの公式では負数の平方根や立方根の意味を新しく与えない限り、この三つの実数解をいずれも得ることができなくなってしまった。

　そこで二次方程式の虚数解が$${a+b\sqrt{-1}}$$の形をしているところから、多くの人が任意の次数の方程式の解も同じ形になっていることを証明しようと試み、三次元方程式の解も同様に試みた。このようにして$${a+bi}$$という複素数の概念が芽を出した訳である。

*1　20010430　複素数(1)
*2　数学の試合と三次方程式の公式
*3　Scipione dal Ferro