
【とある本格派フェミニストの憂鬱10パス目】技術革新と認識革命①記述統計概念からロジスティック回帰概念を経て単純パーセプトロン概念へ
2023年最後の投稿では、積年の課題だった「ロジスティック回帰に至る数理に到達する」を何とか達成する事が出来ました。
これが出来ると何が嬉しいかって、多くの機械学習入門解説が「どうやって予測精度をロジスティック回帰より引き上げるか?」から出発するので機械学習理論登場以前の数理と、機械学習理論登場以降の数理を連続的に語る事が出来る様になるんですね。
そしてこの2024年最初の投稿では、昨年最後の投稿から数理だけを抽出する試みに挑戦したいと思います。
記述統計概念から線型回帰概念へ
以下の投稿でも述べている様に、私は2017年末まで完全に数学の門外漢であり「どうして記述統計学の自明の場合の延長線上としてニューロンコンピューティング概念が登場するか」すら説明出来ない様な有様だったのです。
こうして2017年末に「自分の考え方には徹底して数理が足りてない」と自覚して数学再勉強を誓う展開を迎えます。
やっとこの問題の解答を得たのは昨年、すなわち2023年末になってからでした。要するに、ある意味「相関係数が十分高い二次元評価軸(x,y)については、ニュートンラプソン法(最小二乗法)によって背景に一次方程式y=ax+bを想定し、傾きaと切片bを求める意味が生じる」というのが既存の記述統計学の到達点となります。

なお「ニュートンラプソン法(最小二乗法)によって傾きaと切片bを求める」辺りから計算が急激に煩雑となり、多くの人間が「面倒な計算はコンピューターに任せればいい」という結論に到達する。
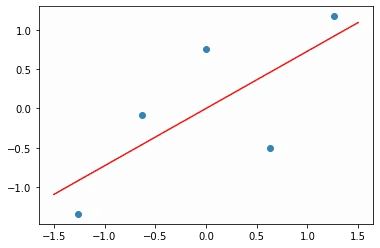
その一方で機械学習初心者は、このプロセスを例えば「自明の場合として身体サイズが大きいペンギンは体重も重い」などのデータセットを用いて学び、同時に「コンピューターに処理させるデータを下準備する苦労」などを実際に体験する。
しかしながら、こうやって抽出された相関関係は擬似相関(Spurious relationship,)かもしれません。
例えば実際には背後にさらに第三の評価軸zが存在し、評価軸xも評価軸yもこれと相関しているだけで、評価軸xと評価軸yの間には直接の相関が存在しない可能性について検討してみよう。
より具体的には二次元評価軸xzとyzそれぞれの残差(residual)、すなわち背景に仮定された一次方程式ax+bの理論値と実測値の差を求め、その相関係数を取り直す事によってこれを調べる。
ここで使われる第三の相関係数を偏相関係数(Partial Correlation Coefficient)といいます。
こういうケースの最も著名な例は「計測すると各県の映画館数と病院数の間に高い相関係数が出るが、実際には両者は人口と相関しており、この部分を除いた偏相関係数を求めるとそれほど高くない(よって擬似相関である)」というもの。
この様に背景に変数が一個しか存在しない一次方程式y=ax+bを想定する場合を単回帰分析(Simple Regression Analysis)、考え方を拡張して複数の変数$${x_n}$$を想定する場合を重回帰分析(Multiple Regression Analysis)といいます。重回帰分析では、背景に想定する式も線型多項式$${y=a_0+a_1x_1+a_2x_2+…+a_nx_n}$$へと拡張される事に。こうして抽出される切片$${x_0}$$と傾き$${a_n}$$の集合を偏回帰係数(Partial Regression Coefficient)といいます。
この問題を解いてそれぞれの傾き$${a_n}$$と切片$${x_0}$$の集合を得るには連鎖律(Chain Rule)を駆使した偏微分の繰り返しが必要であり、ますます多くの人間が「面倒な計算はコンピューターに任せればいい」という結論に到達する事になる。何せデータ項目を1個やし($${x_1,x_2}$$)としただけでこの有様なので…
$$
S_e=\sum_{n=1}^{n}(y_i-(a_0+a_1x_{i1}+a_2x_{i2})^2)
$$
これを丁寧に偏微分していく。
$$
S_{11}=\sum_{n=1}^{n}(x_{i1}-\bar{x_1})^2
$$
$$
S_{12}=\sum_{n=1}^{n}(x_{i1}-\bar{x_1})(x_{i2}-\bar{x_2})
$$
$$
S_{22}=\sum_{n=1}^{n}(x_{i2}-\bar{x_2})^2
$$
$$
S_{y1}=\sum_{n=1}^{n}(x_{i1}-\bar{x_1})(y_i-\bar{y})
$$
$$
S_{y2}=\sum_{n=1}^{n}(x_{i2}-\bar{x_2})(y_i-\bar{y})
$$
最終的に得られるのは…
$$
a_1=\frac{s_{22}s_{1y}-s_{12}s_{2y}}{s_{11}s_{22}-s_{12}^2}
$$
$$
a_2=\frac{-s_{12}s_{1y}+s_{11}s_{2y}}{s_{11}s_{22}-s_{12}^2}
$$
$$
a_0=\bar{y}-a_1\bar{x_1}-a_2\bar{x_2}
$$
なお、各項目の単位が「身長 (cm)」や「体重(kg)」と異なったままでは比例尺度的比較が出来ないので、自明の場合として同時に「正規化」が遂行される。
変数ごとの粒度を揃えるためのデータに対して行われる前処理が正規化(normalization)です。例えば平均と分散を使って、平均値が0、分散が1になるように標準化します(より具体的には、各データを標準偏差で割る)。何故正規化が必要かというと、入力変数の単位(m, mm)や比べる対象(温度、密度)が異なり、そのままの数字を使うと、影響度合いをうまく評価できないからです。
要するに正規化とはそれぞれの評価軸の「増分1」を揃える作業。なお、以降の記述ではネイピア数(2.71828182…)を根とする自然指数関数$${y=e^x}$$概念や自然対数関数$${y=log(x)}$$概念が当然の様に登場してきますが、そもそもネイピア数とは「正規化」概念の大源流、すなわち加法群$${a_n=(a_{-∞}=-∞,…,a_{-1}=a_{0}-1=-1,a_{0}=0,a_{0}+1=+1,…,a_{+∞}=+∞)}$$と乗法群$${a^n=(a^{-∞}=0,…,a^{-1}=\frac{1}{a},a^{0}=1,a^{1}=a,…,a^{+∞}=+∞)}$$の「増分を揃える」魔法の様な係数。これによって元来は-∞と+∞の間に任意に置ける加法単位元(加減算nの基点)0と、同様に-∞と+∞の間に任意に任意に置ける乗法単位元(乗除算の基点)1の間における「増分が1となる関係」が特定され、それぞれの評価次元上の比例関係が射影可能となるのです。
とはいえ、人類が普通にそう考える様になった歴史は浅く、概ね16世紀における常用対数表の刊行までしか遡れなかったりします。契機となったのは、大航海時代欧州における地図や海図の測量や、天体観測における計算の手間の爆発的増大。そして、それを支える科学諸表の作成(およびその校正)があまりにも面倒臭いのでコンピューターが開発される事になったのです。
記述統計の世界から推測統計の世界へ
ここから先話はいよいよ推測統計の世界へと踏み込む事になります。
①ある現象が起こる確率($${0≦P_i≦1}$$)と、その条件($${(x_{i1},x_{i2},…,x_{in}),-∞≦x_{in}≦+∞}$$)のi個の集合からなるデータセットが存在するものとする。

脱線気味の解説を以下に分離。
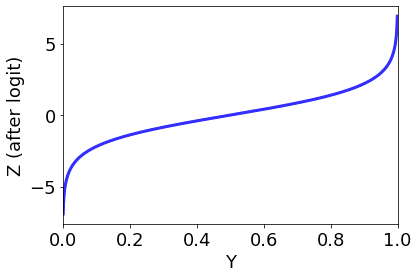
②偏回帰係数$${(a_1,a_2,…,a_n),-∞≦a_n≦+∞}$$を明かにする為に、目的変数Pを確率からオッズ比$${y=log(\frac{P}{1-P}),-∞≦y≦+∞}$$に変換し(ロジット変換)重回帰分析を遂行する。
脱線気味の解説を以下に分離。
③ロジット変換の逆関数たるロジステック変換$${P=\frac{1}{1+exp(a_0+a_1x_1+a_2x_2+…+a_nx_n)}}$$によって出力を確率に戻す。

そう、実はある意味、上掲の「常用対数表を使って面倒な掛け算/割り算を比較的簡単な足し算/引き算に変換し、計算後戻す」考え方の応用に他ならないのである。
この計算方法をロジスティック回帰分析(Logistic Regression Analysis)と呼ぶ訳です。
機械学習概念へのパラダイムシフト
上掲の様に偏回帰係数を重回帰分析によって算出するロジスティック回帰分析は、まだまだあくまで観測データの線形性を当てにした線型予測の一種。
しかしもう一度、その計算過程の全体像を振り返ってみましょう。
ある現象が起こる確率($${0≦P_i≦1}$$)と、その条件集合($${(x_{i1},x_{i2},…,x_{in}),-∞≦x_{in}≦+∞}$$)で構成されるi個のデータを使って偏回帰係数$${(a_1,a_2,…,a_n)を求める=「学習する」。
新たな説明変数$${x_1,x_2,…,x_n}$$を与えられると、目的変数yとして確率Pを返す=「学習結果に従って推測する」。
人間の目にはこういう「教師あり学習」としても映る訳で、まさにこのインターフェイスこそが「機械学習」概念の出発点となったのでした。
そして新たに現れたニューラルネット・コンピューティング概念の観点から遡って線型回帰分析は「線形関数$${y=a_0+a_1x_1+a_2x_2+…+a_nx_n}$$を活性化関数に使った単純パーセプトロン」、ロジスティック回帰分析は「シグモイド関数$${y=\frac{1}{1+exp(a_0+a_1x_1+a_2x_2+…+a_nx_n)}}$$を活性化関数に使った単純パーセプトロン」と規定されその仲間に加えられる展開を迎えたのです。
簡単に要約すると、ロジスティック回帰の返す目的変数は確率P。それが(あらかじめ設定しておいた?)閾値を超えているかいないかで判別してTrue(1)かFalse(0)のニ値を返すのが単純パーセプトロンという認識。
しかも興味深い事に、上掲で扱った「経済学における効用概念」もまた、このフォーマットに落とし込めそうだったりする。

考えてみれば、上掲の図にも現れておる様に「財の消費量が増大するにつれ、得られる満足感は次第に減少する」なる限界効用逓減の法則を文字通り解釈すれば、その真逆たる「財の入手可能性が下がれば下がるほど、その財についての渇望感は急激に、文字通り幾何級数的に増大する(筈)」なる「逆(?)限界効用逓減の法則」も想定可能なのが自明の場合。これについて、少なくとも人口爆発問題については「適正値1への収束」が観測可能としたのが以前の投稿で触れたロジスティック方程式の概念であり、ここからさらに分岐したのが「シグモイド曲線を描く識別関数を活性化関数に採用したロジスティック回帰分析」となる。
だがこのパラダイムシフト、色々な既存概念を大胆に切り捨てる事で成立した様な気がしてなりません。反進歩主義的? そもそも進歩主義と反進歩主義的の関係は? この辺りの話が今年の投稿の課題となる事が明らかとなった辺りで以下続報…
この記事が気に入ったらサポートをしてみませんか?
