
天才の条件とは何か?(中編)
前回、天才の条件とは何か?(前編)で、天才の条件について考察してきたが、今回の中編では、前回定義づけた三条件を基準に踏まえ、真の天才を探っていく事にする。
まず始めに、第一条件を確認しよう。
天才の第一条件:英才教育や身を置く環境など、外的な要因のみでは予想しえない顕著な能力を有する者
世界の歴史上、数々の超人的な能力を持つ者が地球に存在してきた。
しかし、その中からあえて選ぶとすれば、この第一条件の筆頭候補として、私はジョン・フォン・ノイマンを挙げたい。
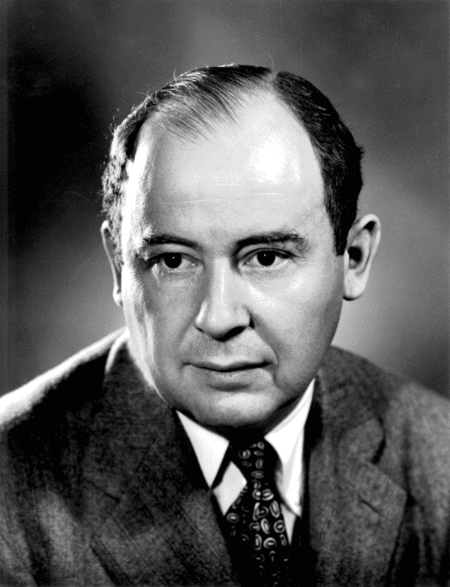
ジョン・フォン・ノイマン
(画像出典:Wikipedia)
ノイマンはハンガリー出身の数学者であり、現在のパソコンの基本構造「ノイマン型コンピューター」を考案し、経済学では「ゲーム理論」を提唱した人物として名高い。
彼のあまりに突出している能力とは、そのあまりに異質な先天的頭脳であり、子供の頃は遊び半分で分厚い電話帳を丸暗記、8歳の頃には微積分法をマスターし、12歳の頃には関数論(大学で習う数学教材)を読破、さらにノイマンは、ブダペスト大学・スイス工科大学・ベルリン大学の三つの大学に在学し、数学の学位だけでなく科学の学位まで取ってしまうという離れ業をやってのけている。
その後ノイマンは、数学者としての道を歩む事になるのだが、彼の功績は数学だけに留まらず、物理・経済・生物・気象・政治学などにも影響を与え、その計り知れない功績と頭の良さに火星人、悪魔の頭脳の持ち主、という名称まで付けられた。
ノイマンの天才性を表す有名なエピソードとしてこんな話がある。
ノイマンがマンハッタン計画に携わっていたとき、物理学者のエンリコ・フェルミとリチャード・P・ファインマン(両方ノーベル賞受賞者)と3人で水爆の効率概算を競った。ファインマンは手回し式計算機を使い、フェルミは計算尺を使い、ノイマンは暗算で挑んだが、その結果、ノイマンの答えが最も早く正確だった。
また、自身が開発したコンピューターと計算勝負をして打ち負かし、数学者が3ヶ月の苦闘の末に解いた問題を数分で解いたりと、その伝説は数知れない。

ノイマンの推定IQは300と言われている
画像出典:math.info
世界の歴史上、先天的素養の持ち主は数多存在してきたが、これほどまでに異質な能力を持ち得ている者は、私の知る限りではまずいない。よって、天才の第一条件に該当する第一人物は、ジョン・フォン・ノイマンとする。
天才の第一条件に該当する人物:ジョン・フォン・ノイマン
次に第二条件を確認しよう。
天才の第二条件: 努力の中に狂気を宿した者
第二条件のポイントは、ある対象に対してどれだけ取り憑かれたかのような努力と行動をしてきたかという点であるが、その人物として私はエヴァリスト・ガロアを推薦したい。ガロアは1811年フランス生まれの数学者で、群論を用いて5次以上の方程式に普遍的な解の公式は存在しない事を発見した人物として有名である。

エヴァリスト・ガロア
(画像出典:Wikipedia)
ガロアは16歳の頃にルジャンドルの書いた数学教材『幾何学の基礎』に影響を受け数学を勉強し始めたが、読破するまで2年かかるとされるこの本をたった2日で読破し、17歳の頃には『ジュルゴンヌ年報』という数学の一流専門誌に論文(循環連分数についてのある定理の証明)が掲載されるようになった。ガロアの解法はあまりにも革新的で洗練されており、多くの計算を論証プロセスを踏む事なく暗算ですました為、担任講師は以下のような評価をしている。
「彼は数学の狂気に取り憑かれてしまっている。したがって私の意見では彼がその全エネルギーを数学に注ぎ込むよう、彼の両親を説得するのが良いと思う。彼はこの学校で時間を浪費している。彼のする事といったら、教師たちをいらつかせ、絶えず処罰しなければならないよう仕向けるばかりである。」
実際にガロアの数学的才能はあまりに時代を先駆けており、フランスの名門校エコール・ド・パリ入学試験時には、試験官がガロアの飛躍した回答についていけなかった為、ガロアが試験管に黒板消しを投げつけ不合格になったという逸話があるほどである。
※これについては試験数日前にガロアの父が亡くなった影響で動揺し、試験に落第したとの説が現在有力である。
そんな天賦の才に恵まれたガロアであるが、彼の人生は至って不遇の連続で、アカデミーへ3度も論文を提出したにも関わらず、査読者の突然死によって論文が紛失し、さらに再度提出された論文もその証明が理解されずリジェクトされている。また、フランス革命後という動乱の最中に生まれた事もあり、ガロア自身も政治活動にのめり込み、その結果退学処分を受け、20歳の頃には恋愛関係のもつれから決闘を挑まれ命を落としている。
ガロアは決闘前夜、証明式を完成させる為に筆を走らせ、こんな遺書を友人に向け最後に書き残している。
~共和主義の同志たち~
愛国者たち、友人たちよ、国のためでない理由で死にゆくことを非難しないでほしい。
僕は破廉恥な娼婦(coquette)と、その女に欺かれた二人の人の犠牲者として死ぬのだ。惨めな影口の中で私は命を落とすのだ。
ああ!なぜそんなつまらないことのために、そんな卑劣なことのために死ななければならないのだろう!
あらゆる手段を講じて避けんとした挑発に屈することを強いられたと天は証言するだろう。冷静には聴いていられないような破滅的な事実を君たちに知らせることを申し訳なく思う。しかしついに僕は真実を語ったのだ。虚妄と、そして愛国の地に対するはっきりした意識を持って僕は墓に入ろう。
さらば!僕は公益のために良い人生を送ってきた。
僕を殺す者を許し給え、彼らは誠実な人たちなのだ
パリ、1832年5月29日
(p.268-269)
-加藤文元『ガロア-天才数学者の生涯』-
~オーギュスト・シュヴァリエへ~
親愛なる友よ、
僕は解析学においていくつか新しいことをやった。
そのいくつかは方程式論に関するもので、他のいくつかは積分で表される函数に関するものだ。
方程式論においては、僕はどの方程式がべき根で解けるのかを研究した。これによってこの理論を深める機会を得、べき根では解けない場合も含めて、方程式に作用する可能なすべての変換を書き出すことができた。
これらすべてを三つの論文にまとめることができる。
(中略)
親愛なるオーギュスト君、君も知っているように、これらが僕の探求したすべての題目ではない。僕の思索の中心は、最近は超越解析の曖昧の理論への応用に向けられている
(中略)
しかし僕には時間がない。僕のアイデアはこの広大な分野において十分に発展されたとは言えないのだ。
この手紙を百科全書詩に体裁してほしい。
僕は人生の中で自分が十分に確信の持てない命題を提示するという危険をしばしば冒してきた。しかしここに書いたことはすべて僕の頭にあってもうすぐ一年になる。それに僕が完全には証明しきれてない定理を公言していると疑われるのは僕の望むところではない。
ヤコビかガウスに、これらの定理の正しさではなく重要性について、公の場で意見を求めてほしい。
その暁には、この乱雑な記述を読み解いて利になることを見出す人々も出てくるものと期待している。
ほとばしる心を込めて君を抱きつつ。
(p.270-272)
-加藤文元『ガロア-天才数学者の生涯』-

決闘の前日に書いたとされる数式
翌朝、ガロアは挙銃を手に恋敵と対峙する事になるが、腹部を打たれ病院へ搬送されたが腹膜炎を起こし、最後に弟のアルフレッド・ガロアにこのような言葉を残し亡くなっている。
「泣くな。二十歳で死ぬ為にはあらん限りの勇気が必要なのだ」
不遇の人生に巻き込まれながらも数学に対する信念を貫き、明日自分が決闘で死ぬとわかりながらもその前夜に筆を懸命に走らせ証明式を書き上げる心境とは一体如何ほどのものだろうか。ガロアの担任教諭がいったように、まさに数学に対する狂気こそがガロアを突き動かし、その狂気と才能によって現代数学の礎となるガロア理論を打ち立てたといっても過言ではないだろう。よって、ここでは天才の第二条件に当てはまる人物をエヴァリスト・ガロアと定めたい。
天才の第二条件に該当する人物:エヴァリスト・ガロア
次回後編では、天才の第三条件に当てはまる人物を選定し、これら三条件に最も近しい人物を真の天才と位置付ける事にする。
参考文献
参考リンク
この記事が参加している募集
この記事が気に入ったらサポートをしてみませんか?
