CADで幾何学

CADで円弧を書くことを覚えるのに、こういう算数の問題はどうだろう。

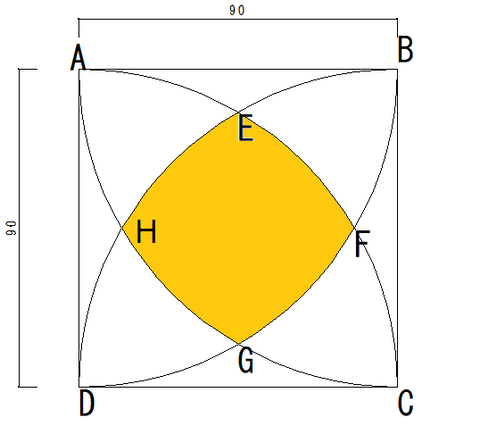
単位はCADなのでｍｍではあるが、この黄色の図形の周囲の長さを求めよというのが小学生の知識で解けるそうだ。
円周率を「3.14」として必要ならば使って解いてよいということだ。

まずCADでこの図形を描く。
一辺9㎝（90㎜）の正方形は命令があるので難なく描ける。
問題は円弧（4分の1円）である。
円の命令はあるが、その横に「円弧」の命令もあった。
これは使うのにコツがあって、まず中心を指定する。
最初はAの点を指定し、反時計回りに円弧の支点Dを指定し、次に終点のBを指定するのである。
これで弧DBが描ける。
必ず反時計回り指定していくところがCADソフトの決まりのようだ。

で、この問題は小学生にとっては難問らしく、有名中学を目指す子なら、模擬試験で何度も出会っているはずで、私も塾に備えてある問題集から取った。
私はCADの練習のために、おもしろい図形を探していたのだ。
これを解くには補助線を引くのだが…
そのために、弧の長さは円周の長さの公式から導かれるということを知識として必要である。
円周＝２×半径×円周率　…①
解析的に言えば、円周を半径R距離から円の中心まで積分したものが円の面積Sであり、
S＝πR²　…②
これを微分すれば、円周Lが出る。
L＝２πR　…③
と、これは小学生には難しすぎるので、公式を暗記させるほかない。
そして弧の長さは扇形の弧の長さのことであり、それは同じ半径の円の中心角を円の部分と考え、360度分の何度という比を円周に掛けたものが弧の長さとなる。
ラジアンを学べば、もっと理解が深まると思うが、まあそれは小学生には早い。
図面屋はラジアン表記も使うので、慣れておかねばならないが。

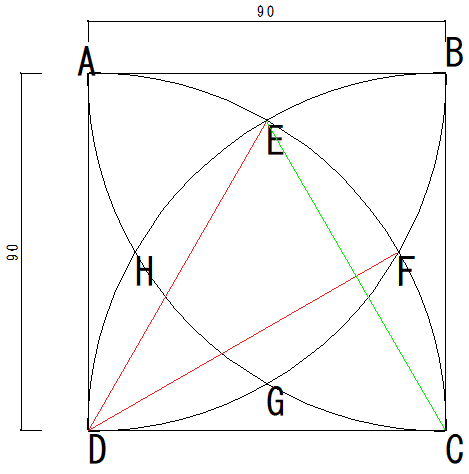
ここまで図に描けば、もう明らかだろう。
△DECは各辺が半径9cmと同じで正三角形となる。
ゆえに∠EDC＝60°である。
すると∠ADEは30°だ。
DからFに引いた線分は、△DECを二等分し、∠FDC＝30°である。
とうぜん、∠EDF＝30°である。
弧EFの長さは
EF=２×π×9×30／360＝540π／360＝3π／2＝1.5π＝4.71
それが四つあるから、
4.71×4＝18.84（㎝）となる。
中学生なら6πで答えとしてもよい

さて、黄色の図形の周の長さを求めたが、それならこの黄色の図形の面積はいくらなんだ？という疑問が当然湧いてくるはずだ。
それには、まず、以下の黄緑色の部分の面積を求めるという、教科書に必ずと言っていいほど載っている問題を解く必要がある。

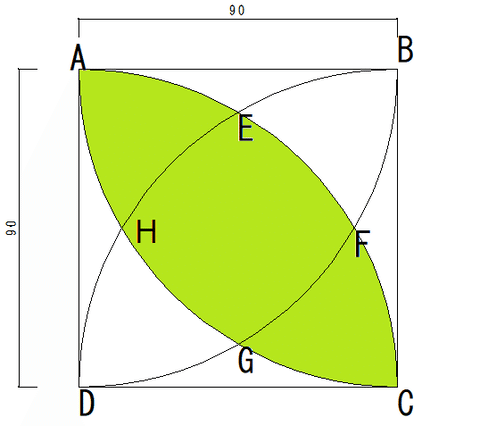
この場合、直接この黄緑色の図形の面積を求めることが気づきにくい子は、正方形から以下のピンク色の面積を求めて二倍した面積を引く（取り除く）と目的の面積が得られるという方法だろう。

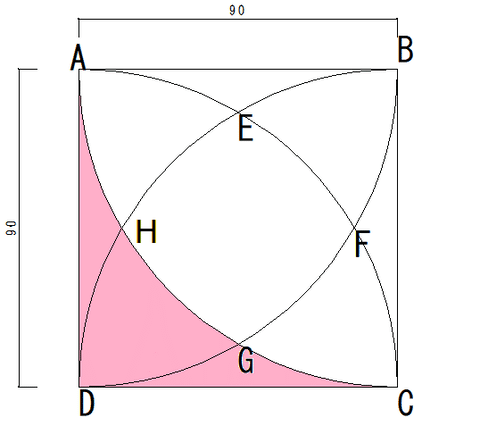
勘のいい子は、扇形ADCの面積から△ADC(直角二等辺三角形）の面積を引いて、二倍するというエレガントな方法で解くだろう。
扇形ADCの面積Pは
P=3.14×9×9÷4=63.59（㎠）
△ADCの面積Qは
Q=9×9÷2＝40.5(㎠)
図形AEFCGH（黄緑色の部分）の面積Rは
R＝2×(63.59-40.5)=46.18(㎠)
言うまでもないが、この黄緑色の図形の周の長さは半径9㎝の円の半周分であり2×3.14×9÷2＝28.26(cm)である。

さて、本題の黄色の図形の面積であるが、これを求めるには「勘の悪い子」が求めたピンク色の図形の面積が必要になってくる。
まず以下の茶色の部分の図形の面積が知りたいのだが、

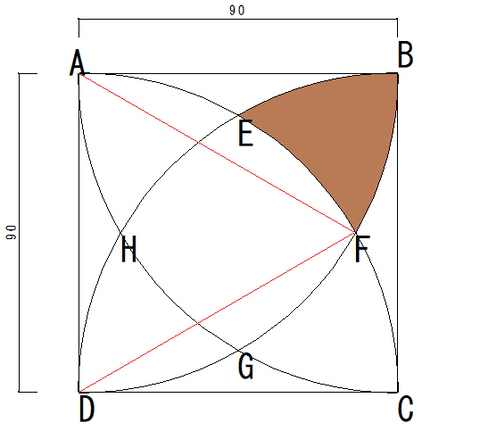
そのためには、先に灰色の部分の面積を知る必要がある。

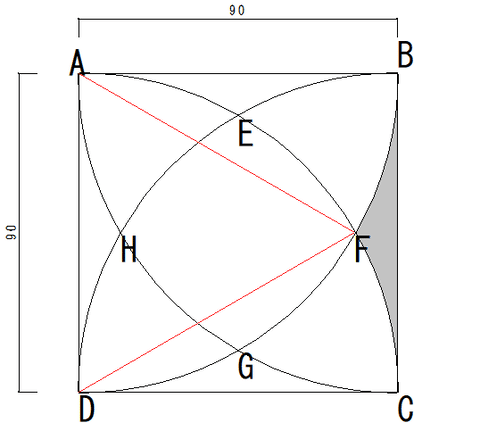
灰色の部分、図形BFCの面積は、9×9の正方形から扇形ABFとそれに合同な扇形DFC、そして1辺の長さが9の△AFD（正三角形）を除いたものだ。
扇形ABF（扇形DFC）の面積Tは∠BAFが30°である（∠FADは正三角形の角で60°ゆえ）から、
T＝3.14×9×9×30°／360°＝21.2(㎠）
△AFDの面積は、点Fと点Hを結んだ直線の延長と辺ADの交点をJとすると、線FJは辺ADの直角二等分線でありかつ、△AFDの高さとなり、直角三角形△AJFは底辺：高さ：斜辺＝１：√３：２である。
すると△AFDの高さｈは
√３：２＝ｈ：９よりｈ＝9√３/２
△AFDの面積をUとすると
U＝9×9√３/２÷２＝81√3/４＝35.03(㎠）
図形BFCの面積Vは
V＝9×9－35.03－21.2×２＝3.57（㎠）
ゆえに茶色の面積は、ピンク色の面積から灰色の面積の倍を引いたものだ。
ピンク色の部分の面積をMとすると
M＝9×9－3.14×9×9÷4＝81－63.59＝17.41（㎠）
茶色の部分の面積をNとすると
N＝M－2×V＝10.27（㎠）

すると、次の水色の部分の面積から茶色の部分を引いてやれば、最初の黄色の部分の面積がでるはずだ。
※いや、黄緑色の部分から茶色の部分の面積の二倍を引くだけでいいんちゃう？とは、和多田塾頭のご意見でした。なるほど…

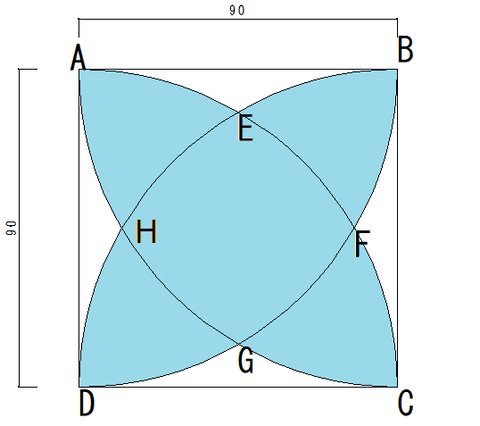
水色の部分の面積Kは正方形ABCDから灰色の部分の4倍を引いたものだ。
K＝81－4×3.57＝66.72(㎠）
ここからさらに茶色の部分の面積の4倍を引くと黄色の部分の面積が出る。
66.72－4×10.27＝25.64(㎠）
計算間違いがなければ、合っていると思う。

途中どうしても√３が出現するので、中学生以上でないとこの問題は解けないことになる。
昔から、この正方形内の扇形が作る、不定形の面積やその周の長さを求めさせる出題は多く、受験界では「手垢のついた問題」とされている。