ストロークの球速・ポジションとショット到達時間の関係

TOMOHITO

2023年10月16日 23:09

こんにちは、トモヒトです。

今回は、ストロークの球速・ポジションがショット到達時間にどのような影響を及ぼすかをみてみます。

検証方法

定数（物理定数、用具）

重力加速度=9.81m/s^2
空気密度=1.21kg/m^3
反発係数=0.75
摩擦係数=0.72

ボール半径=0.033m
ボールの質量=0.0577kg

変数

球速：90km/h～160km/hの範囲で5km/h刻み
ショットの打ち出し角度：1～19.8度の範囲で0.2度刻み
回転量：900～2550回転の範囲で50回転刻み
座標：アドサイドのシングルスサイドラインとベースラインの交点を、(0, 0)として、xに関してはデュースサイド方向を正、yに関してはネット方向を正とする
打点の高さ=1m

ショット到達時間に関しては、ベースライン後方2mのラインを越えるか、2バウンドしたときの時間とし、球速ごとに最短の到達時間を算出します。

import pandas as pd
import numpy as np

def search_shot(sv, swing_angle, spin, net_height, shot_distance):
    ball_radius = 0.033  # ボールの半径 (メートル)
    A = np.pi * (ball_radius**2)  # ボールの断面積 (m^2)
    m = 0.0577  # ボールの質量 (kg)

    shot_v = sv / 3.6

    w = spin * (np.pi / 30)

    net_length = shot_distance[0]
    net_height += ball_radius

    shot_length = shot_distance[1]
    bound_length = shot_distance[2]
    hitting_point_distance = shot_length + bound_length

    # 物理定数
    g = 9.81  # 重力加速度 (m/s^2)
    rho = 1.21  # 空気密度 (kg/m^3)
    e = 0.75  # 反発係数
    myu = 0.72  # 摩擦係数

    v0 = np.zeros(4)
    v0[1] = 1
    v0[2] = shot_v * math.cos(math.radians(swing_angle))
    v0[3] = shot_v * math.sin(math.radians(swing_angle))

    t_min = 0
    t_max = 5
    dt = 0.001
    t = np.arange(t_min, t_max, dt)
    t_span = (t_min,t_max)

    solved_data = solve_ivp(f, t_span, v0, t_eval=t, args=(ball_radius, w, rho, m, g, A))

    flag = True

    for i in range(len(solved_data.t)):
        if solved_data.y[0, i] >= net_length - 0.02 and solved_data.y[0, i] <= net_length + 0.02 and solved_data.y[1, i] <= net_height:
            return np.nan, np.nan, np.nan
        if solved_data.y[1, i] <= ball_radius:
            if solved_data.y[0, i] <= net_length:
                return np.nan, np.nan, np.nan
            elif solved_data.y[0, i] <= shot_length:
                shot_time = solved_data.t[i]
                reach_time = solved_data.t[i]
                y2 = np.zeros(4)
                y2[0] = solved_data.y[0, i]
                y2[1] = solved_data.y[1, i]
                y2[2] = solved_data.y[2, i] * e - myu * g
                y2[3] = - solved_data.y[3, i] * e
                if solved_data.y[2, i] - w > 0:
                    w = w - myu * g
                elif solved_data.y[2, i] - w < 0:
                    w = w + myu * g
                break
            else:
                return np.nan, np.nan, np.nan

    solved_data = solve_ivp(f, t_span, y2, t_eval=t, args=(ball_radius, w, rho, m, g, A))

    flag = False
    for i in range(len(solved_data.t)):
        if len(solved_data.t) == i - 1:
            break
        if solved_data.y[1, i+1] - solved_data.y[1, i]:
            flag = True
        if solved_data.y[0, i] >= hitting_point_distance or (flag and solved_data.y[1, i] <= ball_radius):
            bound_time = solved_data.t[i] + 0.004
            reach_time += solved_data.t[i] + 0.004
            return shot_time, bound_time, reach_time


def f(t, y, ball_radius, w, rho, m, g, A):
    u, udot = y[:2], y[2:]
    v = np.sqrt(udot[0]**2 + udot[1]**2)

    # 抗力係数
    Cd = 0.508 + (1 / ((22.503 + 4.196 * (v / (ball_radius * w)) ** 2.5) ** 0.4) )
    # 揚力係数
    Cl = 1 / (2.02 + 0.981 * (v / (ball_radius * w)))

    udotdot_x = ((A * rho * v) / (2 * m)) * (- Cd * udot[0] + Cl * udot[1])
    udotdot_y =  ((A * rho * v) / (2 * m)) * (- Cd * udot[1] - Cl * udot[0]) - g
    dydt = np.hstack([udot, udotdot_x, udotdot_y])
    return dydt

import itertools

columns = ["shot velocity", "shot angle", "spin rate"]
df = pd.DataFrame(columns=columns)
v = [x for x in range(90, 165, 5)]
a = [x for x in np.arange(1, 20, 0.2)]
s = [x for x in range(900, 2600, 50)]

for i, comb in enumerate(itertools.product(v, a, s)):
    df.loc[i, columns] = list(comb)

x = 0  "左右の位置"
y = 0  "前後の位置"

for i, l in enumerate([23.77/2+6.4, 23.77/2+6.4+((23.77/2-6.4)/2), 23.77]):
    print(l)
    # Near Side
    if x == 0:
        bound_l = l - y
        net_l = 23.77/2 - y
        shot_l = 23.77 - y + 2
        net_height = 1.042
    else:
        bound_l = np.sqrt((l - y) ** 2 + x ** 2)
        net_l = bound_l * (((23.77/2) - y) / (l - y))
        shot_l = bound_l * ((23.77 - y + 2) / (l - y))
        net_height = min(1.07, 0.914 + (0.156 * (((8.23 / 2) - x + (np.sqrt((net_l ** 2 - ((23.77/2) - y) ** 2)))) / 5.029)))

    result_columns = [f"shot time near{i}", f"bound time near{i}", f"reach time near{i}"]

    df[result_columns] = df[columns].apply(
        lambda x: search_shot(x[0], x[1], x[2], net_height, [net_l, bound_l, (shot_l - bound_l)]),
        axis=1,
        result_type="expand"
    )

    # Far Side
    bound_l = np.sqrt((l - y) ** 2 + (8.23 - x) ** 2)
    net_l = bound_l * (((23.77/2) - y) / (l - y))
    shot_l = bound_l * ((23.77 - y + 2) / (l - y))
    net_height = min(1.07, 0.914 + (0.156 * (abs(((np.sqrt((net_l ** 2 - ((23.77 / 2) - y) ** 2) + x)) - (8.23 / 2))) / 5.029)))

    print(bound_l, net_l, shot_l, net_height)

    result_columns = [f"shot time far{i}", f"bound time far{i}", f"reach time far{i}"]

    df[result_columns] = df[columns].apply(
        lambda x: search_shot(x[0], x[1], x[2], net_height, [net_l, bound_l, (shot_l - bound_l)]),
        axis=1,
        result_type="expand"
    )

今回は、以下の図の4方向のショットで球速・ポジションを比較します。
比較対象のポジションは、ベースライン後方0.5m、ベースライン上、ベースライン前方0.5mの3点からです。

結果

結果に関しては、コースごとの傾向は同じであったため、near2を例にみていきます。

ストレート方向のショット（near2）

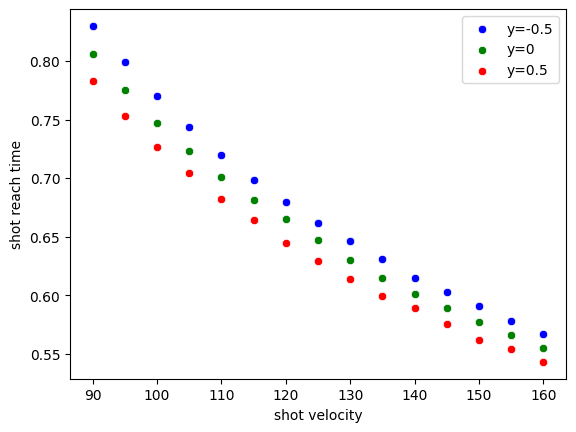
y（コートの前後）のポジション別に、球速ごとのショット到達時間をグラフに表すと、下の図になります。

ポイントとしては、以下の2点です。

グラフは右肩下がりになっているが、傾きは右にいくほど小さくなっている
→ショットスピードが上がるほど、+5km/hでの到達時間の短縮幅が小さくなる
右にいくほど、同じショットスピードでのポイント間の幅が小さくなっている
→ショットスピードが上がるほど、ポジションの前後による到達時間の変化が小さくなる

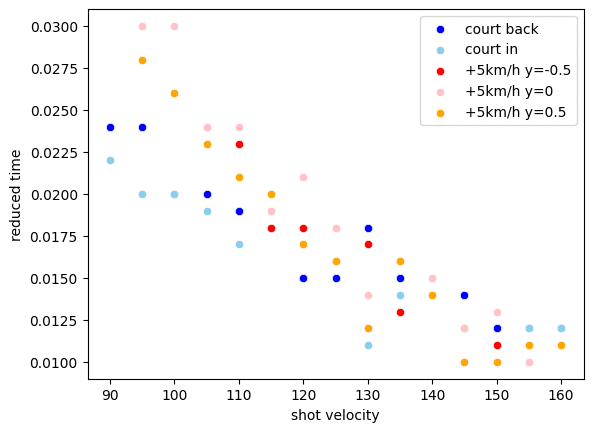
条件ごとの到達時間短縮幅は、以下のグラフのとおりです。
court back => y=-0.5とy=0の間での到達時間の差分
court in => y=0とy=0.5の間での到達時間の差分
+5km/h y=* => ショットスピード-5km/hとの到達時間の差分