素数螺旋に関する予想4 対数関数を用いてフォームチェンジされる素数螺旋が、強敵レピュニットナンバーズに再戦を挑む……っ! 勝て、今一度螺旋の力を見せるのだっ!
色んな数列と比較しようと思い、レピュニット数と比較することにした。
但し、レピュニット数は幾何級数的に増大するので対数化することにした。

これが、螺旋の力なのか……。
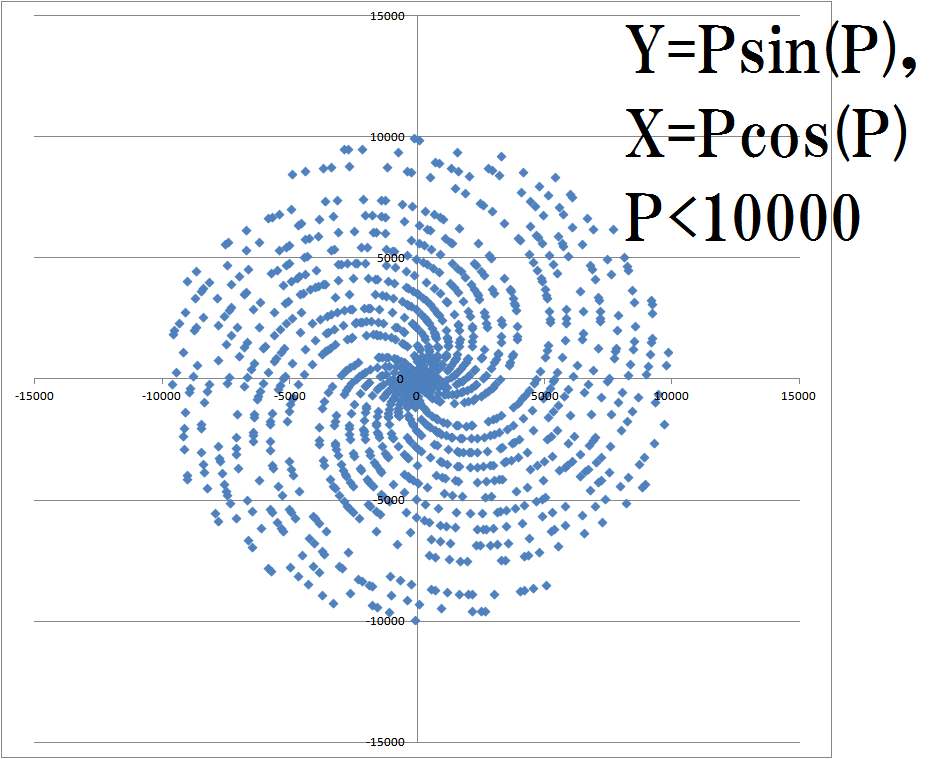
比較対象としての素数螺旋。

尚、無限遠方において、これはほぼ連続的な曲線とみなせることになるだろう。
対数化されしレピュニット数螺旋について、この螺旋が上手く潜り抜け続けるのなら、レピュニット素数は有限であることになる。
大体、フィボナッチ数にしても、N^2型数についても、
この、”素数螺旋の密なエリア”(何と定義したらいいだろう?)と、重なる確率が高くなれば、その数列に素数が存在することになるので、素数螺旋の面積についての話は、ある数列に素数が含まれているかどうかという話とリンクしているのかも知れない。
……たとえば”素数螺旋の密なエリア”に対して、充分多くの点が、ある程度以上ランダムに打たれるのなら、素数が存在する確率が高くなる。
問題は、”素数螺旋の密なエリア”に対して、”ある数列の密なエリア”が重なる部分が無限に存在するかどうかだろう。……そうして、どういった風に重なるのか?
観察してみたい。
