宮城県｜公立高校入試確率問題2018

　右の図のように円周上に４点Ａ，Ｂ，Ｃ，Ｄがあります。点Ｐは円周上を動く点で，はじめ点Ａの位置にあります。１枚のコインと，１個のさいころを同時に１回投げたとき，点Ｐは，次の［　］に示したとおりに，円周上の４点を，Ａの位置からＢ，Ｃ，Ｄ，Ａ，Ｂ，…の順に動くものとします。

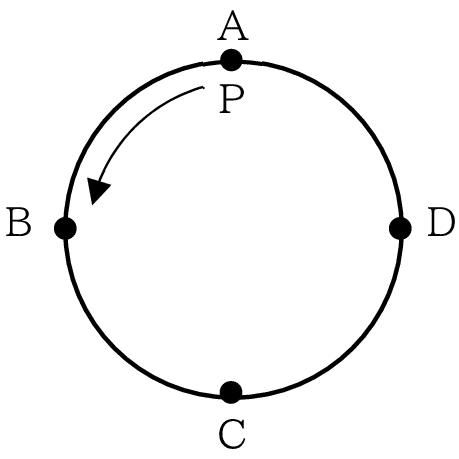
・コインの表が出たとき，点Ｐは，さいころの出た目の数だけ動く。
・コインの裏が出たとき，点Ｐは，さいころの出た目の数を２倍した数だけ動く。

　たとえば，コインの表が出て，さいころの出た目の数が１のとき，点Ｐは点Ｂまで動きます。
　この，１枚のコインと１個のさいころを同時に１回投げるとき，次の（１），（２）の問いに答えなさい。
　ただし，コインは，表と裏のどちらが出ることも同様に確からしいものとし，さいころは，１から６までのどの目が出ることも同様に確からしいものとします。
（１）　コインの表と裏の出方とさいころの目の出方の組み合わせは，全部で何通りありますか。
（２）　点Ｐはどの点まで動く確率がもっとも大きいか答えなさい。また，その確率を求めなさい。

分類：応用〈２〉　動かす②　循環型

問題を解く前に

（１）

　コインとさいころという、２つの別々の偶然発生装置を使うパターンです（基礎編１７）。表はこんな感じになりますね。

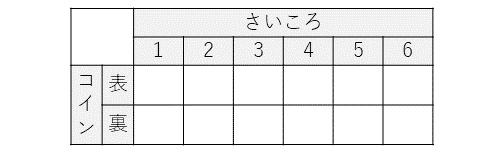
　マス目を数えて１２通り。

（２）

　問題に書いてあるルールに従って、いくつ動くかを計算すると、

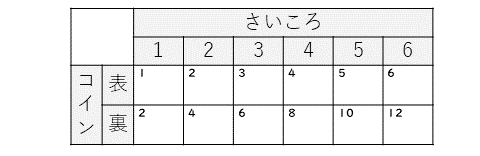
それだけ動いた跡に、どこにいるかを書くと、

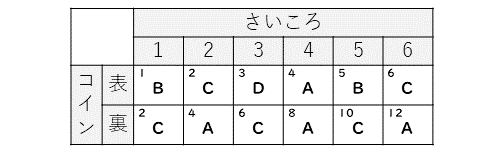
いちばんどこの点に動く確率が高いかというと、Ｃですね。

確率は、$${\bm{\dfrac{5}{12}}}$$

（１）　１２通り　　　（２）　点Ｃで、その確率は　$${\bm{\dfrac{5}{12}}}$$

※応用編〈２〉の採録例題から，こちらに変更。