基礎編６＊　「分子判定の基礎①」並べて２けたの整数をつくる

　　大小２つのさいころを同時に１回投げ，大きいさいころの出る目の数を十の位の数，小さいさいころの出る目の数を一の位の数としてできる２けたの数を$${m}$$とするとき，$${m}$$が素数である確率を求めなさい。
　ただし，さいころの目の出方は１，２，３，４，５，６の６通りであり，どの目が出ることも同様に確からしいものとする。（三重県2020）

問題を解く前に・・・

　ここからは、分子の出し方に焦点を当ててみようと思います。

　そのためには、分母は「さいころ２個／２回」の問題（分母は３６になる、基礎編３・４・５）だけにして、分子の求め方、分子はいくつになる？に集中して解説したいと思います。

　実は，ここまでは２つの偶然の結果を直接比べたりする問題でした。しかし多くの確率の問題は「いったん判断材料を作って、それを判定する」というタイプの問題です。

　分子も、やはりいくつかのパターンに分けて、見ていくことにしましょう。まずは「２けたの数をつくる」問題。

分母は・・・

　基礎編３でやったように、３６通りですね。

分子は・・・

①判定材料をつくる
　　↓
②それを判定して、数える
というやり方で進みます。（ここまで採り上げてきた問題は，実は判定材料をつくるところが省略できる問題を選んできていた、というわけです。）

①判定材料を作る

　これまでの問題と違うのはいったん判定材料を作る、ということです。

　この問題の判定材料は、問題文にあるとおり大きいさいころの出る目の数を十の位の数，小さいさいころの出る目の数を一の位の数としてできる２けたの数 $${\bm{m}}$$です。

　さっきの表にそれぞれつくった２けたの数を埋めていきましょう。

分子②・・・判定して数える

　さて、材料ができましたので「素数かどうか」を判定して、数えましょう。素数かどうか？　２でわれるかな、３でわれるかな、５でわれるかな、７でわれるかな・・・とやっていけばいいのですが、カンのいい人は気づいたかも知れません。一の位が２・４・６のときは偶数になるので、素数ではありません。（２は素数ですが、ここでは２けたの整数を考えているので、こう言っても大丈夫）

　それから、一の位が５のときも５の倍数になるので、素数ではありません。（５は素数ですが、ここでは２けたの整数を考えているので、こう言っても大丈夫）

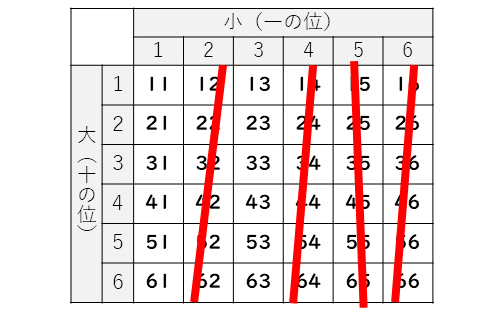
　残っているのは、一の位が１か３の数。この中で３とか７とか１３とか・・・でわれない数を探せばよいのです。数え漏らしがないように、いらないものはどんどん消していく方法の方が、この場合はよさそうですね。

　というわけで、素数は次の８つ。分子は８

　ちなみに５１は３でわり切れるので、注意してね。

答えは・・・

$${\dfrac{8}{36}}$$ = $${\bm{\dfrac{2}{9}}}$$

答　　$${\bm{\dfrac{２}{９}}}$$

問題を解いた後に・・・

　「２けたの数をつくる」問題の中には、

★偶数や５や１０の倍数など一の位だけで判断できる問題
★３の倍数を判断する問題

のように、いちいち２けたの数を列挙するよりも早く解くショートカットがあります。それは後ほど【研究】として取り上げることにします。

　とりあえず，ここではいろんなパターンに触れるために先を急ぎます。

－－－－－－－－－－－－－－－－－－－－－－－
＜前の問題　　　　　次の問題＞
問題一覧

類題　　滋賀県2021、佐賀県2021