
基礎編12* 「分子判定の基礎⑥」代入その2
1から6までの目が出るさいころを2回投げて,最初に出た目の数を$${x}$$,2回目に出た目の数を$${y}$$とする。このとき,$${2x-y-5=0}$$が成り立つ確率を求めなさい。
ただし,さいころはどの目が出ることも同様に確からしいものとする。(徳島県2020)
問題を解く前に・・・
「うっ 文字式・・・方程式・・・」と思う人もいるかもしれませんが、確率の出し方はいっしょ。淡々と「分母はいくつ?」「分子はいくつ?」と考えていきます。
分母は・・・
「さいころを2回」なので、表はこうなります・・・で大丈夫でしょうか? ダメだったら基礎編4を。

なので、分母は 36
分子は・・・
分子はいろいろ考え方があると思いますが、とりあえず $${2x-y-5}$$ を計算して、これが0になるかどうか、ということでやってみましょう。
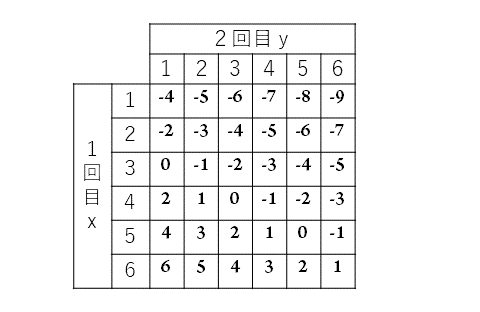

というわけで、条件に合う場合は3つなので、分子は 3
答えは・・・
$${\dfrac{3}{36} = \bm{\dfrac{1}{12}}}$$
$${\bm{\dfrac{1}{12}}}$$
問題を解いた後に・・・
とりあえずこのnoteの目的は、まずは素朴に確率の問題を解く方法をお伝えする、そのうえで、早く解く方法がないか研究をする、ということなので、上の解き方はちょっとまどろっこしく感じた人もいるかも知れません。
判断材料について、$${2x-y-5=0}$$を変形して$${2x-y=5}$$にしておいて、$${2x-y}$$を計算すると5になるかどうか、という方が速かったかも知れませんね。問題をたくさん解いて慣れてくれば、そういう楽の仕方、近道も思いやすくなるでしょう。
-----------------------
<前の問題 次の問題>
問題一覧
この記事が気に入ったらサポートをしてみませんか?
