神奈川県｜公立高校入試確率問題2016

　右の図１のように，円Ｏの周上に，円周を１２等分する点Ａ，Ｂ，Ｃ，Ｄ，Ｅ，Ｆ，Ｇ，Ｈ，Ｉ，Ｊ，Ｋ，Ｌがある。
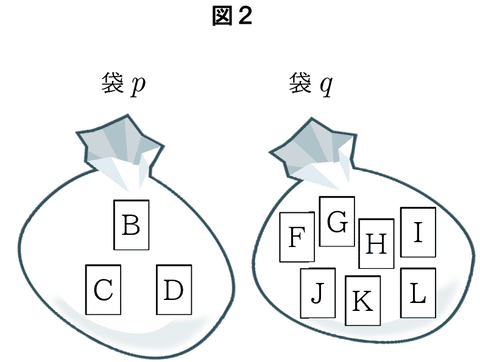
　また，図２のように，２つの袋$${p}$$，$${q}$$があり，袋$${p}$$の中にはＢ，Ｃ，
Ｄの文字が１つずつ書かれた同じ大きさの３枚のカードが入っており，袋$${q}$$の中にはＦ，Ｇ，Ｈ，Ｉ，Ｊ，Ｋ，Ｌの文字が１つずつ書かれた同じ大きさの７枚のカードが入っている。
　袋$${p}$$の中からカードを１枚取り出し，そのカードに書かれた文字と同じ文字の図１の点の位置に点Ｐをとり，袋$${q}$$の中からカードを１枚取り出し，そのカードに書かれた文字と同じ文字の図１の点の位置に点Ｑをとる。
　いま，２つの袋$${p}$$，$${q}$$の中からカードをそれぞれ１枚ずつ取り出すとき，次の問いに答えなさい。ただし，それぞれの袋の中から，どのカードが取り出されることも同様に確からしいものとする。
（ア）　線分ＰＱが円Ｏの中心を通る確率を求めなさい。
（イ）　∠ＡＰＱの大きさが60°以上となる確率を求めなさい。
（ウ）　三角形ＡＰＱが二等辺三角形となる確率を求めなさい。

分類：《Ｂ２》円周角

（ア）起こりうるすべての場合は・・・？

　まずは、２つの偶然が起こりますから、表をかいて考えましょう。袋ｐから取り出す偶然と、袋ｑから取り出す偶然とは、お互いに影響はしませんので、表は下のようになります。

　起こりうるすべての場合は２１通りで、そのいずれが起こることも同様に確からしいです。そのうち、線分ＰＱが円Ｏの中心を通るのは、ＢＨ・ＣＩ・ＤＪの３通りです。

　したがって確率は$${\dfrac{3}{21}=\bm{\dfrac{1}{7}}}$$と求めることができます。

（イ）円周角→中心角で考えると

　ここでは∠ＡＰＱが円周角であることに、まず気がつきましょう。すると、円周角が６０度以上ですから、対応する中心角∠ＡＯＱが１２０°以上であればいいわけです。つまり、Ｐは関係なく、Ｑのことだけ考えればよいので、∠ＡＯＱが１２０°以上になるＱはＦ・Ｇ・Ｈ・Ｉの４通り（Ｉのときに１２０°）となります。ですから求める確率は$${\dfrac{4}{7}}$$です。

（ウ）二等辺三角形ということは

△ＡＰＱが二等辺三角形になるには
①　ＡＰ＝ＡＱ
②　ＡＰ＝ＰＱ
③　ＡＱ＝ＰＱ
のどれか１つがあてはまればよいわけです。もう一度表をかいて考えましょう。

というわけで、求める確率は$${\bm{\dfrac{5}{21}}}$$です。

答

（ア）$${\bm{\dfrac{1}{7}}}$$　　（イ）$${\bm{\dfrac{4}{7}}}$$　　（ウ）$${\bm{\dfrac{5}{21}}}$$