
基礎編15* 「2つ取り出すの分母③」同時に2個取り出す
数の書いてある5枚のカード1,2,3,4,5が箱に入っている。この箱から2枚のカードを同時に取り出すとき,取り出した2枚のカードに書いてある数がともに奇数である確率はいくらですか。どのカードが取り出されることも同様に確からしいものとして答えなさい。 (大阪府2012前期)
問題を解く前に・・・
前回の基礎編6・7と違うところを見てみましょう。
○取り出して、戻してもう一度(基礎編13)
○取り出して、戻さずもう一度(基礎編14)
○2枚同時に取り出す(←いまここ)
2つの偶然を起こすので、AさんとBさんの2人で分担してもらいましょう。
分母は・・・
AさんとBさんが2人で分担します







だけど、


同じカードを取り出す,ということはできませんね。

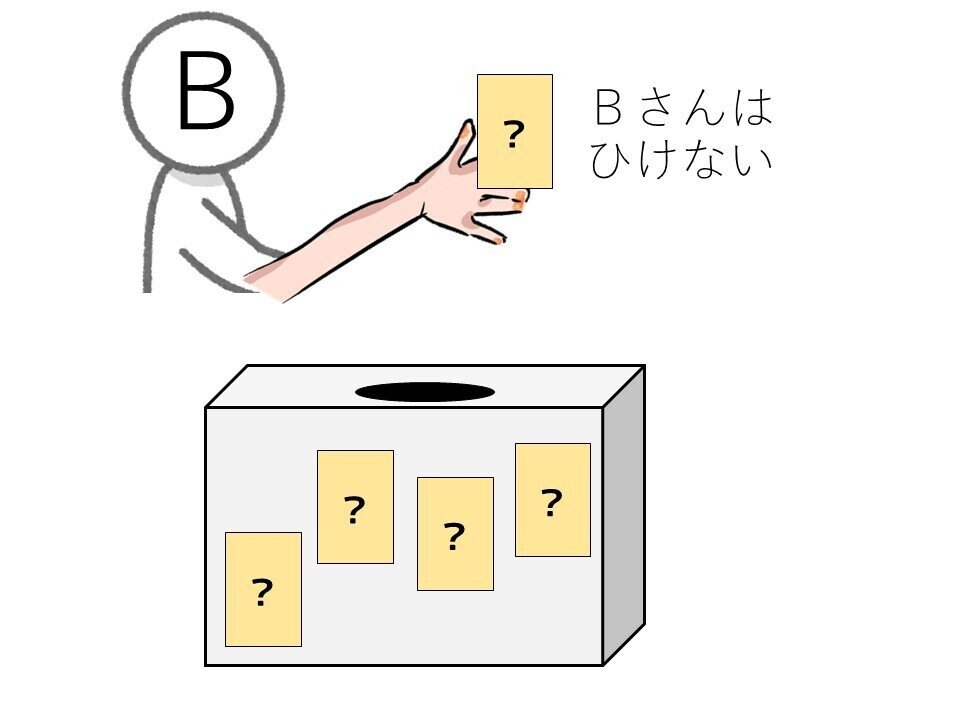


でも・・・さらに,こんなこと気になりませんでしたか?

もともと同時に2枚取り出すのを、無理やり2人で分担する、と考えているわけです。
が、ここに、ちょっと楽をするヒントもあります。2人は別々のカードを取り出さないといけないのですが、2人の順番は関係ありません。なので、この2つの場合は
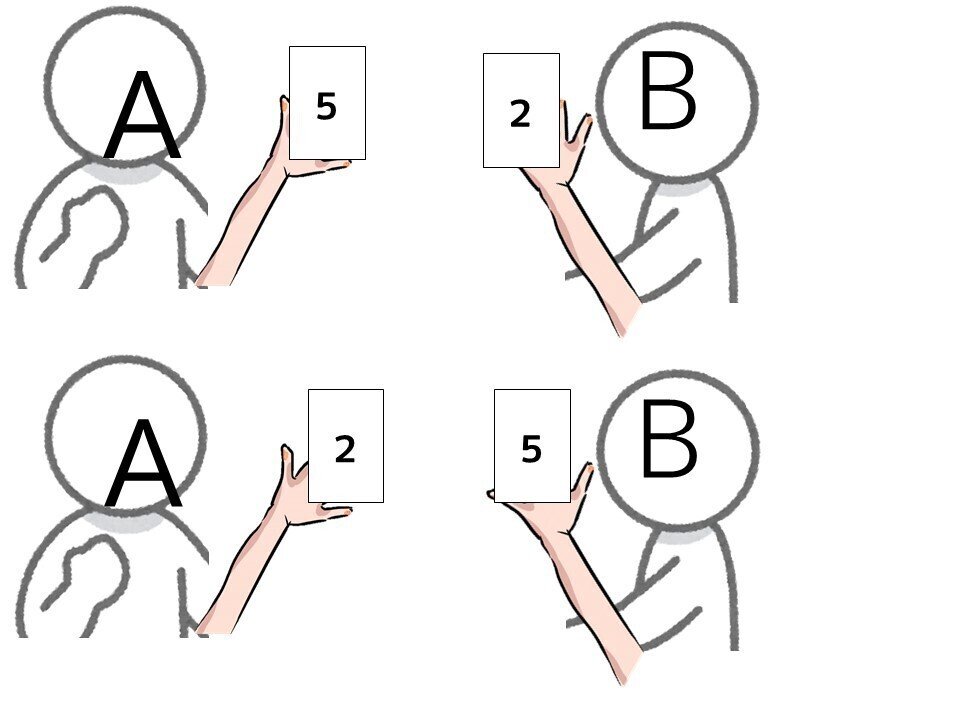
いっしょのこと、と考えていいのです。
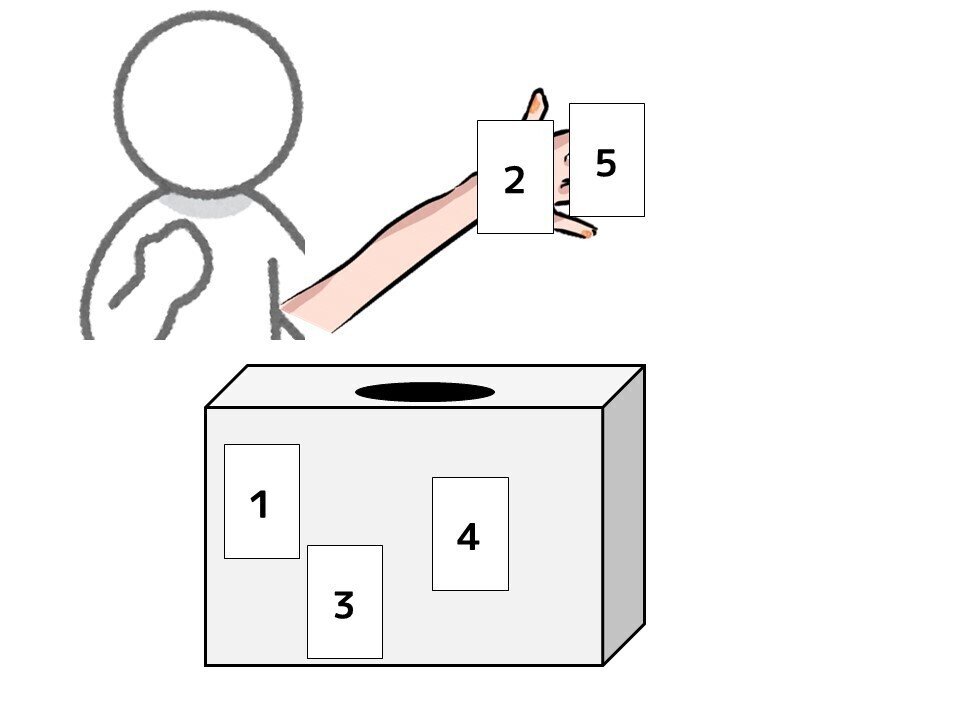
表に戻ると、同じ色を塗ったところは、結局同じこととしてまとめることができます。

たとえば[1-2]と[2-1]はおんなじ、・・・のように2つ1組と考えてまとめてしまうと、2つのうち1つに代表してまとめてしまうことができます。ここではたとえば[1-2][2-1]のうち、Aさんが小さい方を引いた方[1-2]を残しておくことにしましょう。(どっちを残すか、のルールを決めておくのは、重要ですよ)
すると、表でみると、右上だけが残ります。

できる起こるすべての場合は、半分の10と考えることができますね。分母は10です。
分子は・・・
さあ,分母のマス目が決まったところで,この中で「当たり」の印をつけていきましょう。この分母の中であたりの印をつけることが重要です。今回の当たりは,2つともが「奇数になる」場合でしたね。表に印をつけた〔1-3〕〔1-5〕〔3-5〕の3つの場合になります。

答えは・・・
3/10
問題を解いた後に・・・
2個同時にとり出す,という問題もよく出ます。「Aさんが2,Bさんが5」と「Aさんが5,Bさんが2」の場合を同じ1つのセットにまとめて考えるということになります。
重要なのは,すべての場合において2つの場合を1セットにしてまとめることができる、ということです。こっちは3つを1つ、こっちは4つを1つのセットに・・・というのではなくて、必ず2つを1セットにする、と言うことができる、と言うことです。だから、全部をセットにしてしまって、2つの場合を1つのセットにまとめたものの方で考えよう! そんな発想です。だから、この問題では「すべての場合」を半分にして考えることができる、というわけです。
同様に確からしいものを並べる発想を忘れないように。
そして、間違えないようにするポイントが、表を左下を消して半分にしてで数えるか、消さない形で数えるか、です。消さない形で考えてみると

6/20=3/10 約分すれば求められる確率はいっしょです。
とりあえず偶然2つのときは「楽をするかしないか?」ぐらいで済みますが、高校以降の「組合せ」の考え方を頭に置くと、(2,5)の取り出し方と(5,2)の取り出し方、順番に意味があるか無視していいか、という考え方は、ふまえておいた方がいいのでは? と思います。
問題を解いた後に その2
このように、ドッチがどっちを引いたかは関係ない、順序が関係ない取り出し方を考えるとき、高校の数学では組合せといいます。英語ではcombination(コンビネーション)。頭文字はCですね。
なので、ここでも、AさんBさんの順序が関係ない取り出し方のことをC型と読んでおきましょう。2つ取り出す表の場合は、2つの場合が1セットになり、すべての場合の数は順番が関係するとき(P型)の半分になります。
-----------------------
<前の問題 次の問題>
問題一覧
類題 千葉県2023 山梨県2023 静岡県2022 滋賀県2022 福岡県2022 山形県2021 大阪府B2021 静岡県2020 愛媛県2020
この記事が気に入ったらサポートをしてみませんか?
