
電力システムの同期現象を数理科学する〜数学の削ぎ落とす哲学
本稿では、電力システムで発電機集団の周波数が同期するという現象を「数理科学の視点」で解説します。微分方程式という小難しい概念が登場しますが、高校数学で習う微積分の知識が少しあれば理解できるように工夫しました。記事の最後に「数理科学でエネルギー問題を考えること」への私の信条も書き添えています。ダ・ヴィンチの『シンプルさは究極の洗練である』やファン・デル・ローエの『Less is More』、アップルの『Think Simple』などの言葉に心惹かれる方はそこだけでもご一読ください。
■ はじめに
これまでの記事では「数学と物理で考える」と謳っているにも関わらず数式なしで電力システムの性質を解説してきました。文章の説明だけでは物足らないという特異点近傍の読者に向けて、今回は少しだけ数学してみようと思います。
メイントピックは、非線形科学から生まれた「蔵本モデル」と呼ばれる微分方程式系の紹介です。蔵本モデルは「周波数が自動的に同期する現象」を表現する有名な数理モデルです。微分方程式系と聞いて身構える必要はありません。基本的には高校数学で習う微積分の知識が少しあれば理解できるように私なりに解説してみたいと思います。
蔵本モデルを紹介した後で、簡単に発電機の同期現象との関係を説明します。発電機の同期現象って何? と気になった方は、こちらの解説も気が向いたときに読んでみてもらえると嬉しいです。
■ 有名なメトロノームの同期現象
非線形科学という分野で研究されている同期現象でわかりやすいものはメトロノームの同期です。バラバラに揺れていたメトロノームたちが、台座を経由して相互に影響し合うことで、次第に「シンクロ」します。
注意深く見てみると、揺らした直後のメトロノームの周期(音楽的に言えばBPM)はそれぞれバラバラです。にもかかわらず、時間が経つと同じ周期に一致して、左右に揺れるタイミングもほぼ一致します。不思議ですね。
■ メトロノーム単体の数学的表現
では、このような同期現象を数式で表現することを考えてみましょう。何らかの現象や対象の挙動を数学的に表現したものは「数理モデル」と呼ばれます。準備として、まずは1つのメトロノームが一定の周期で揺れている状況を表現してみます。カチカチカチ...と一定の周期で揺れるような周期現象は「円周上を一定の速度でクルクル回る点」を考えるとスッキリと表せます。
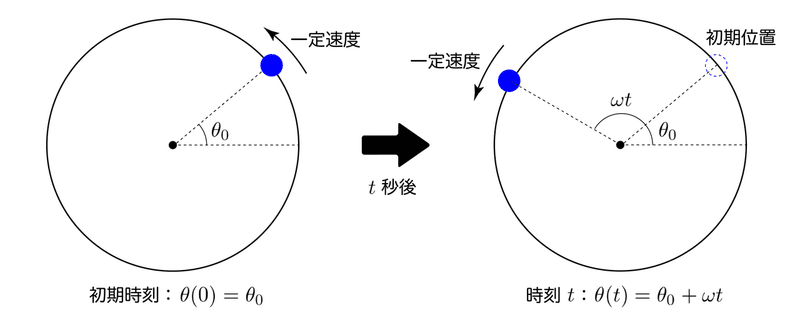
この図のように、青の点が一定の角速度$${\omega}$$で円周上を周回しているとき、1周にかかる時間である周期は一定になります。メトロノームの例で言えば、針が左右に振れることは、青の点が時計でいう3時と9時の方向を行き来していることのように考えられます。ちなみに「角速度」は角度$${\theta}$$が増加する速度を意味します。この例では、角速度$${\omega}$$が一定なので、角度$${\theta}$$は$${t}$$秒間に$${\omega t}$$だけ増えます。以下では、数学用語を使って角度$${\theta}$$のことを「位相」と呼びます。
■ メトロノーム単体の微分方程式表現
青の点の動きを「微分方程式」で表現してみましょう。難しそうですが身構える必要はありません。単純に、時刻$${\boldsymbol t}$$の関数として表されている位相$${\boldsymbol \theta}$$を時間微分すれば、$${\boldsymbol{ \theta(t)}}$$の挙動を表現する微分方程式が得られます。
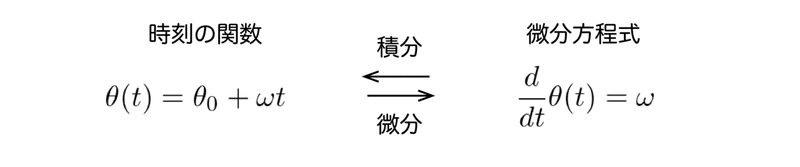
やっていることは1次関数の微分です。高校数学の微積分で一番最初に習うやつです。左側の表現では位相$${\boldsymbol \theta}$$の挙動を時刻$${\boldsymbol t}$$の関数として「直接的」に表現しているのに対して、右側の表現では「時間に関する変化率は定数$${\boldsymbol \omega}$$である」と指定することによって「間接的」に位相$${\boldsymbol \theta}$$の挙動を表現しています。
このように「時間微分=時間に関する変化率」が満たすべき関係を方程式として与えたものが「微分方程式」です。時間に関する変化率を指定することによって、現象や対象の時間変化を間接的に表現することができます。あえて間接的に表現する理由は、その方が多くのモノを簡潔に表せるからです。具体的には以下で説明していきます。
■ 蔵本モデルによるメトロノーム集団の数学的表現
メトロノーム1つの挙動を微分方程式で表せたので、それを3つ集めて来ましょう。動画のように5つの場合も同様です。各メトロノームは互いに影響しない場合にはそれぞれ異なる角速度(BPM)で揺れるものとします。動画のように揺れが互いに影響する動く台座ではなく、堅い床などに並べる場合はメトロノーム間の相互作用はありません。その場合には、下図の左側のように各々の位相(針の位置)は一定で異なる固有角速度で動き続けます。
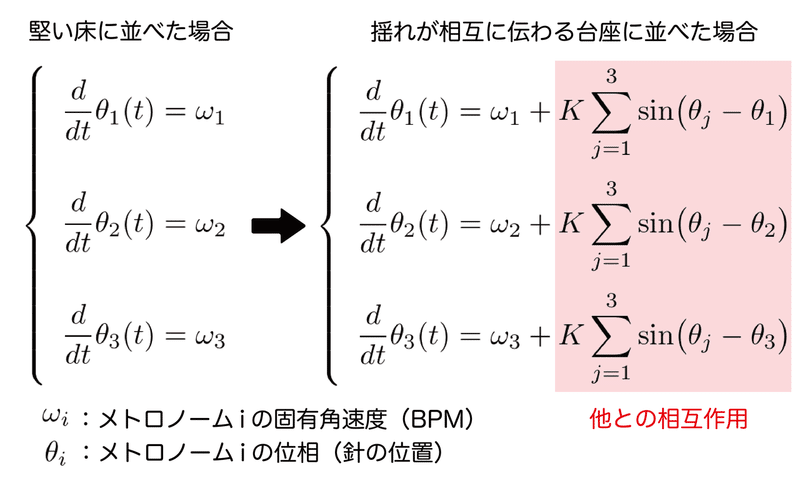
一方で、揺れが伝わる台座に並べた場合には、メトロノームの位相が他のメトロノームの位相と互いに影響します。その相互作用を表したのが画像の右側で赤く示した部分です。ここで$${K}$$は相互作用の大きさを表す定数です。一般に、複数の微分方程式が連立されたものを「微分方程式系」と呼びます。
理解を深めるため、1つ目のメトロノームに注目してみましょう。メトロノーム1はBPMに相当する固有角速度$${\omega_1}$$で針を動かしていますが、針の位置に相当する位相$${\theta_1}$$が他のメトロノームの位相$${\theta_1, \theta_2}$$とズレている場合は、固有角速度$${\omega_1}$$を微調整するような作用を受けます。具体的には、位相$${\boldsymbol{\theta_1}}$$が$${\boldsymbol{\theta_2}}$$や$${\boldsymbol{\theta_3}}$$よりも進んでいる場合には、角速度を下げるような作用が働きます。このようにして、すべてのメトロノームが同じ角速度に「同期」しようとするのです。
この同期現象を表現する数理モデルは、物理学者の蔵本先生によって提唱されたものであり「蔵本モデル」と呼ばれています。下記のインタビューにはどのような思いで研究をされていたのかがわかるので興味深いです。
■ 微分方程式系で表現することの意義
さて、複数のメトロノームが同期することを模式化する数理モデルが得られましたが、各々の位相$${ \boldsymbol{\theta_1}, \boldsymbol{\theta_2}, \boldsymbol{\theta_3}}$$は具体的に時刻$${\boldsymbol t}$$のどのような関数となるのでしょうか? その答えは
テストの解答のように具体的な関数の形を明示することは一般にできません
です。裏を返すと「関数形が明示できない」というところが、微分方程式系という表現形式を使うことのポイントにもなります。
メトロノーム単体の挙動は、位相$${\theta(t)}$$が時刻$${t}$$の単純な1次関数として表現できるので、あえて微分方程式で表現する必要はありません。しかし、複数のメトロノームが相互作用する場合には、各々の位相$${\theta_1(t),\theta_2(t),\theta_3(t)}$$は時刻$${t}$$の単純な関数では表現できません。にもかかわらず「微分方程式系」という形式では、蔵本モデルのように簡潔に表現することが可能なのです。
このように、時刻の単純な関数では表せない現象や対象も「微分方程式系で数理モデル化する」ことによって数学的に明確に表現することができます。メトロノーム集団の挙動も数学的に議論できるようになります。
ちなみに、数学用語では「微分方程式系を満たす解となる時刻の関数」を手計算で理論的に求められないことを「解析的に解けない」と言います。世の中の微分方程式系の大半は解析的には解けないので、具体的に微分方程式系の解を知りたい場合にはパソコンで数値計算します。いわゆる数値シミュレーションというやつです。

数値計算によって、$${x(t)}$$という時刻の関数について、時刻 0 での値、時刻 0.01 での値、時刻 0.02 での値...というように、時刻に紐付いた数値解がデジタルデータとして得られます。得られたデータをえいやと線でつなぐと微分方程式の解となる$${x(t)}$$の「近似的な関数形」がプロットできます。どうやって $${x(0.01)}$$などの数値を計算するのか?については説明は長くなるので省略します。有名な方法はオイラー法やルンゲ=クッタ法です。
■ 同期現象の数学的解析
解析的に解けない微分方程式系についても「微分方程式系を数学的に解析する」ことによって特徴的な性質を見いだせる場合があります。実は、各々の位相$${\boldsymbol{\theta_1(t), \theta_2(t), \theta_3(t)} }$$の関数形は不明ですが、同期する角速度の値は微分方程式系の構造から理論的にわかります。
ポイントはサイン関数が奇関数であることです。要するに
$$
\sin\bigl( \theta_1(t) - \theta_2(t) \bigr) = -\sin\bigl( \theta_2(t) - \theta_1(t) \bigr)
$$
という関係が成り立ちます。この関係により、3本ある微分方程式をすべて足し上げると、サイン関数が含まれる項はすべて打ち消されて
$$
\frac{d}{dt} \theta_1(t) +
\frac{d}{dt} \theta_2(t) +
\frac{d}{dt} \theta_3(t) = \omega_1 + \omega_2 + \omega_3
$$
という方程式が得られます。ここで、位相$${\theta_1(t),\theta_2(t),\theta_3(t)}$$の時間微分である角速度が、ある値$${\omega_{\rm sync}}$$ に十分な時間の経過後に同期すること、すなわち
$$
\displaystyle
\lim_{t \rightarrow \infty} \frac{d}{dt} \theta_1(t)
= \lim_{t \rightarrow \infty} \frac{d}{dt} \theta_2(t)
= \lim_{t \rightarrow \infty} \frac{d}{dt} \theta_3(t) = \omega_{\rm sync}
$$
を仮定しましょう。これを上の方程式に代入すれば、同期する角速度が
$$
\omega_{\rm sync} = \frac{\omega_1 + \omega_2 + \omega_3}{3}
$$
であることがわかります。要するに、相互作用がない場合にバラバラのBPMで動いていたメトロノームは、時間が十分に経過して同期した場合には、固有BPMの平均値に収束することがわかります。これは数学的な解析の結果として得られる帰結です。
■ 電力システムとの関係
だいぶ長くなって疲れてきました。さいごに、電力システムとの関係を簡単に紹介して終わりにしたいと思います。電力システムにおける発電機の原初的な数理モデルはつぎのように書けます。

この2本の微分方程式が単体の発電機を表しているという点に注意してください。例えば、発電機が3台の場合には、2本の微分方程式を3組まとめた計6本の微分方程式が、発電機集団の挙動を表す微分方程式系となります。
蔵本モデルとの大きな違いは、振動子(青の点に相当)の挙動が1本の微分方程式ではなく、2本の微分方程式で表現されている点です。この違いにより、発電機の回転子偏角(位相に相当)の挙動に慣性が現れます。引っ張って動きを止めようとしても惰性ですぐには速度を落とせないため、発電機の周波数は振動的な挙動を示します。
一方で、発電機間の相互作用は蔵本モデルと同様にサイン関数によって表現されています。この数理構造のおかげで発電機の周波数偏差(角速度に相当)が同期します。同期する周波数偏差の値を具体的に計算すると
$$
\omega_{\rm sync} = \frac{P_{{\rm mech}1} + \cdots + P_{{\rm mech}N} }{D_1+\cdots+D_N}
$$
となります。すべてのダンパ係数$${D_i}$$を 1 として、機械的トルク$${P_{{\rm mech}i}}$$を固有角速度$${\omega_i}$$に当てはめれば、蔵本モデルの結果と一致します。ちなみに、発電機の機械的トルクは発電電力の指令値であり、指令値が大きすぎると正の周波数偏差が生じることになります。
■ おわりに〜削ぎ落としの哲学
誤解のないように、本稿で考えた数理モデルの妥当性についてコメントしておこうと思います。メトロノーム集団と発電機集団のどちらの例にも当てはまりますが、紹介した数理モデルが「現象や対象の挙動を完璧に表現するわけではない」という点に注意してください。え?と狐につままれたような感じかもしれません。
動画のメトロノームの同期現象では、よく見るとメトロノーム集団と一緒に台座も動いています。したがって、厳密には台座の挙動を表す微分方程式も必要です。また、すべてのメトロノームは同じ大きさの定数$${K}$$で相互作用するように蔵本モデルでは定式化されていますが、実際には多少なりともバラツキがあるはずです。このように、数理モデルによって現象や対象を完全に表現することは一般にできません。
発電機の例でも同様です。本稿で紹介した数理モデルは、あくまでも周波数偏差の同期現象を数理科学で説明するだけのものです。実際の発電機集団の挙動はもっと複雑です。ちなみに上の数理モデルでは
一部の発電機が電力消費を行うモーターのような想定になっている
消費者による電力消費が含まれていない
内部電圧が定数となっている
送電線における電力損失が考慮されていない
など、実システムの解析で含めるべき要素の大半が考慮されていません。もちろん実用性を重視した研究ではそれらの要素も考慮しています。
では、要素を削ぎ落として考察する数理科学には意味はないのでしょうか? 実際、電力システム関連で数学よりの研究をしていると、実応用に近いエンジニアからは「数理学なんて非現実的で無意味だ」と頭ごなしに否定されることが少なくありません。私としては価値観が合わないなと思います。
でも上の例で言えば「サイン関数による相互作用の構造が発電機の同期現象を原理を説明する」という知見は、数理科学の力で見いだすことができます。このようにして見いだされた数理学的な構造や原理が、新たな技術として応用できる可能性も十分にあります。
このような要素を削ぎ落として本質に迫る考え方は、私が大切にしている信条の1つです。レオナルド・ダ・ヴィンチの言葉を借りれば
『Simplicity is the ultimate sophistication』(シンプルさは究極の洗練である)
です。有名な建築家のミース・ファン・デル・ローエは
『Less is More』(少ない方が豊かである)
とも残しています。Appleの
『Think Simple』(シンプルに考えよ)
にも同じ哲学が感じられます。
これらの考え方に共感をもつ方は、数理科学の世界を楽しめると思います。
以上、長文におつき合いいただきどうもありがとうございました!
▼引き続き関連記事をマガジンに投稿予定です
この記事が気に入ったらサポートをしてみませんか?
