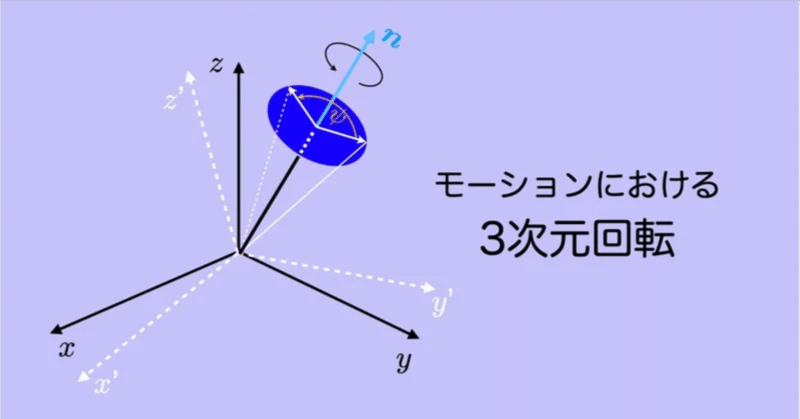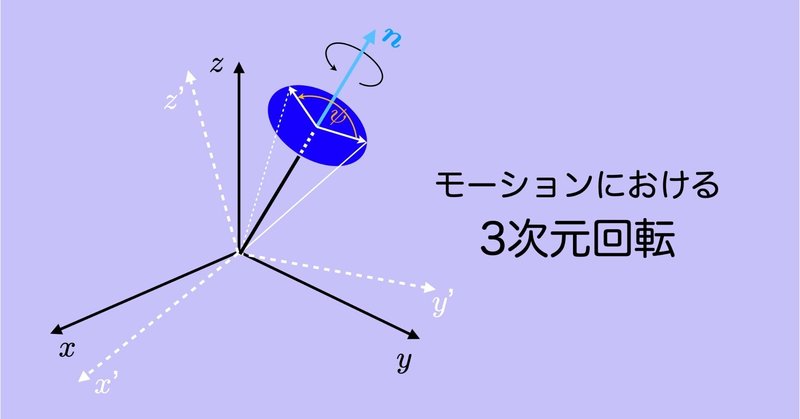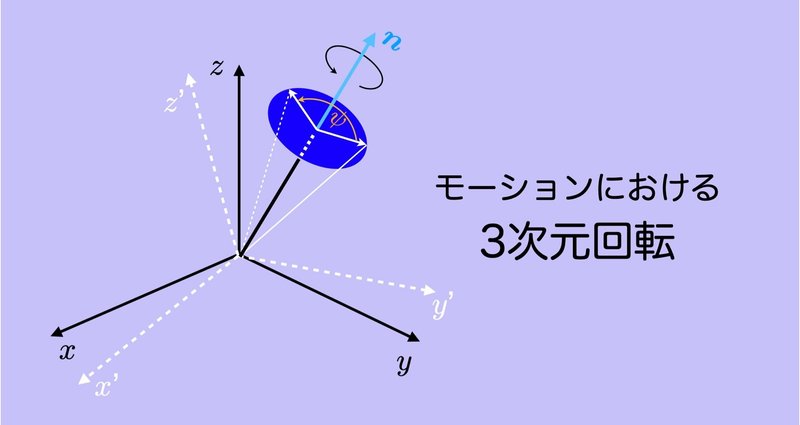
運動計測では,3次元回転に関する数学的理解が不可欠です.しかし,バイオメカニクスの教科書には詳しい解説は見当たりません.単位クォータニオンを中心に他の分野でも書かれていないことも…
- 運営しているクリエイター
#オイラーの公式
モーションにおける3次元回転 #5 〜ロドリゲスの式の幾何学的意味〜
前章「モーションにおける3次元回転 #4 」で,3次元回転を表すロドリゲスの式について述べたが,これは2次元平面の回転を複素数で表すオイラーの公式から単位クォータニオンへの橋渡しと位置づけていたが,もう少し補足する.
復習
図1のように,複素平面で虚数$${i}$$をかけることは,複素平面上の原点まわりの回転を意味する.
例えば,図1の実数軸上の一番右の点である$${1}$$に「虚数 $${i
モーションにおける3次元回転 #3 〜複素数による2次元平面の回転〜
複雑な3次元の回転について説明する前に,複素数を利用した平面内の回転運動について説明する.クォータニオンとは,この複素数を利用した回転表現の3次元空間への拡張であるので,この理解を避けてとおることはできないし,この理解が3次元空間の回転をより深く理解することにつながるはずである.
複素数とオイラーの公式複素数と回転が関係すると言っても,なかなかピンとこないかもしれないが,ここでは,まず,一直線を