
ファイナンス(企業財務)の基本⑯:「リスクの定量化」について、まとめてみた その2
前回から、「事業(企業)価値評価」の「割引率」に関連するところで「リスクの定量化」について、まとめています。今回も、前回の続きで「統計学的な観点」も少し交えて、書いていきたいと思います。
まずは、前回のおさらいです。
ハイリスク・ハイリターンの原則(前回のおさらい)
これまでにも出てきましたが、「ファイナンス(投資)におけるリスク」という言葉を「将来のリターンのばらつきの大きさ」という意味で使うと、下図は、次のように解釈できます。
平均の期待リターンは低いが、リスクの小さいA社
平均の期待リターンは高いが、リスクの大きいB社
この状況は、「投資家にとっては、どちらをより好むかという傾向はあっても、どちらかが一方的に得であるとは言えない状況」です。
株式だけではなく、債券、投資信託など、あらゆる金融資産への投資について、投資家は、リスクの高い投資にはより高いリターンを期待し、逆に、リスクの低い投資では低いリターンで満足します。
これを「ハイリスク・ハイリターンの原則」といいます。
リスクをとることに対する対価を「リスク・プレミアム」といい、リスクの高い投資機会には、より大きなリスク・プレミアムを求めることとなります。

ここから先、「期待リターンとリスク・プレミアムが、どういう関係にあるか?」ということを見ていきます。こちらについて「ポートフォリオ理論」と呼ばれる投資理論がベースになってきます。
ただし、いきなり「ポートフォリオ理論」の話に入ると「よくわからないな・・・」となってしまう可能性が高いです。
そこで、「統計学的な知識」にも少しだけ触れておくことで、後の「ポートフォリオ理論」をスムーズにご理解いただければと思います。
リスク尺度の基本的な考え方
期待値、偏差、分散、標準偏差
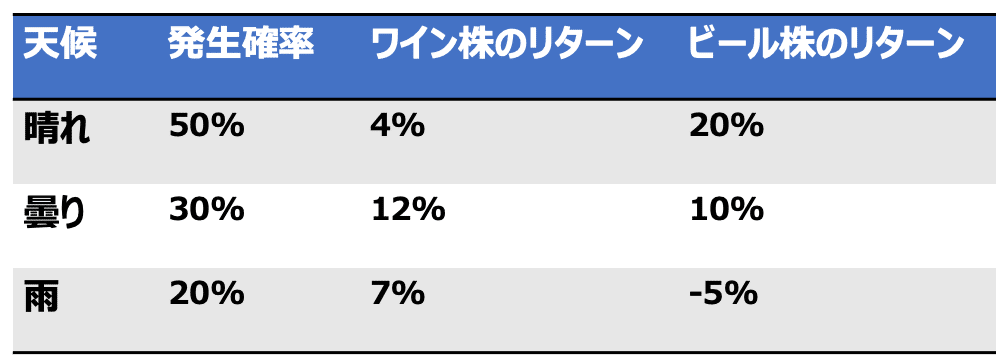
ワイン事業の株式と、ビール事業の株式について考えてみます。
ワイン事業の株式のパフォーマン スは、天候の影響を受けることが予想されます。晴天が多ければ、ビールと競合して売り上げが伸び悩みますが、その他の場合は、概ね堅調です。ただし、雨が多いと消費が落ちるので、その影響を受けます。
過去の株式のリターンを調べたころ、次のような結果を得ました。消費者に大きな変化がなければ、このデータは将来のシナリオとしても有効であるとします。

リターンの期待値
条件に応じて異なるリターンの可能性が考えられる場合、リターンの期待値を求めることで、投資からどの程度のリターンを期待できるかを定量化できます。
期待値とは、将来起こり得るケースのリターンを、起こる確率で加重平均して求めたものです。期待値はEという記号を用いて表現します。期待値という概念自体は、中学校の確率の授業(サイコロの目の問題など)でも、さらっと触れた記憶があります。
E(ワイン)= (晴れの確率 × 晴れのときのリターン)+
(曇りの確率 × 曇りのときのリターン)+
(雨の確率 × 雨のときのリターン)
= (50% × 4%)+(30% × 12%)+(20% × 7%)
= 7%
偏差、分散、標準偏差(リスク = リターンのばらつき度合い)
ワイン株のリスクは「リスク = ばらつき度合い」を定量化することで、測定することができます。ばらつき度合いは、それぞれの状況のリターンと期待値との差をとることから求めます。その差のことを偏差といいます。
偏差 = 各状況におけるリターン - リターンの期待値(平均値)
上式に基づいて、各状況での偏差を計算すると、次のようになります。
晴れの時の偏差 = 晴れのときのリターン - リターンの期待値 = 4% - 7%
曇りの時の偏差 = 曇りのときのリターン - リターンの期待値 = 12% - 7%
雨の時の偏差 = 雨のときのリターン - リターンの期待値 = 7% - 7%
ワイン株の「ばらつき度合い」の平均値を知るためには、偏差にそれぞれの場合の確率をかけあわせ、合計(加重平均)を計算します。
偏差の平均値 =(晴れのときの偏差)× 晴れの確率 +(曇りのときの偏差)×
曇りの確率 +(雨のときの偏差)× 雨の確率
=(4% - 7%) × 50% +(12% - 7%)× 30% +(7% - 7%)× 20% = 0
上に示したように各状況の偏差はリターンの平均値から見てプラスのものもマイナスのものもあるため、偏差の平均を出そうとしても偏差のプラス、マイナスが打ち消しあい、平均値 は「常にゼロ」になってしまいます。
(個人的な解釈としては、上記は、統計学の教科書的な説明の茶番となります)
このため、プラス、マイナスが打ち消しあうことをなくすために、偏差の2乗の期待値を計算します。偏差の2乗のことを分散といいます。
分散 = 偏差の2乗の期待値
分散 =(晴れのときのリターン - リターンの期待値)^2 × 晴れの確率
+(曇りのときのリターン - リターンの期待値)^2 × 曇りの確率
+(雨のときのリターン - リターンの期待値)^2 × 雨の確率
= (4% - 7%)^2 × 0.5 +(12% - 7%)^2 × 0.3 +(7% - 7%)^2 × 0.2
= 12[%^2]
ここで、分散の単位を見ると「%^2」 となっており、他の数値の単位と比較がしにくいため、単位を%にするために、分散の平方根(ルート)をとることにします。これを標準偏差といいます。
標準偏差 = 分散の平方根 = 3.46[%]
共分散と相関係数
今度は、ワイン株に加えて、ビール事業の株も一緒に考えます。
また、ワイン株、ビール株リターンの期待値、偏差、偏差の2乗をまとめると、下表のようになります。

ワインとビールの2つの株を組み合わせて考える場合、この2つの株式のリターンが状況(ここでは天候)の変化に対して、それぞれどういう方向に、どのぐらいの幅で動くのかが、非常に重要です。
上の例で、天候が雨の場合、ワイン株はプラスに動く一方で、ビール株はマイナスに動くというように、ある状況で2つが反対方向に動くと、全体ではぶれ幅が小さい形に収まります。
また、仮に、ある状況で2つが同じ方向に動けば、全体ではぶれ幅が広がるはずです。
このように、ある状況変化に対する各銘柄の動き方は、全体としてのリスクに大きな影響を与えます。
そして、2つ以上の株がどのような関係にあるのかを示す指標が、共分散と相関係数です。
共分散を求めるためには、2つの株のリターンの偏差を掛け合わせ、さらにその確率をかけ合わせて合計します。
共分散 = 晴れのときのワイン株の偏差 × 晴れのときのビールの偏差 ×
晴れの確率 + 曇りのときのワイン株の偏差 × 曇りのときのビールの
偏差 × 曇りの確率 + 雨のときのワイン株の偏差 × 雨のときのビールの
偏差 × 雨の確率
=(-3)× 8 × 0.5 + 5 ×(-2)× 0.3 + 0 ×(-17)× 0.2
=(-12)+(-3)
= -15
共分散を計算すると、プラスまたはマイナスの値をとります。
プラスになった場合には、2つの期待値が同じ方向に動く傾向があることを示しています。
プラスになった場合には、2つの期待値が同じ方向に動く傾向があることを示しています
マイナスの場合には、2つの期待値が逆の方向に動く傾向があることを示しています。
また、共分散の数値(絶対値)は、動く幅を示しています。
共分散の数値(絶対値)が大きい場合には、動く幅が大きいです。
共分散の数値(絶対値)が小さい場合には、動く幅が小さいです。
すなわち、共分散とは動きの大きさと方向の両方を示す指標となります。
なお、動く方向だけを知りたい場合は、相関係数を使うことが多いです。
相関係数は、 次の式で表します。(実際には、excelの関数などでさくっと計算することが多いと思います)
相関係数
= (2つの株式の共分散) /
(ワインのリターンの標準偏差 x ビールのリターンの標準偏差)
相関係数は、共分散と同様にプラスとマイナスの符号を持つことになります。
数値としては-1から+1の間の数値を必ず取ります。
相関のイメージを図で示すと、以下のようになります。

今回は、ここまでにします。
次回は、「リスクの定量化」のメインディッシュである「ポートフォリオ理論」に入っていきます。
