
【初心者向け】音楽で学ぶ、はじめての音声解析
こんにちは。Nishikaデータサイエンティストの中山です。Nishikaでは2020年12月2日より「クラシック音楽の作曲家分類」というコンペティションを開催しております。メタデータなしの純粋な音源のみでクラシックの作曲家を当てることができるか?というタスクになります。
Nishikaでははじめて音声解析がテーマのコンペティションを開催するのですが、画像処理やテーブルデータのに関しては実装したことあるけど音声解析は初めてという方も多いのではないでしょうか。そのような人のためにこの記事ではニューラルネットワークで音声を学習するために必要な処理について解説していきます。対象としている人は「ニューラルネットワークの概要は理解しているが、音声解析は行ったことがないよ」という人です。MNISTやCIFAR10のチュートリアルを動かしたことある方であれば十分に理解できる内容だと思います。
この記事では音声解析の前処理の方法について紹介するだけで、実際に学習するところまでは言及しておりませんが、Nishikaのコンペティションのサイト上では、実際に音源をCNNを使って分類するコードをチュートリアルとして公開しております。また参加者の方からは、音声解析で有効な学習済みモデルの情報提供も頂いており音声解析について学ぶのにうってつけの場であるかと思います。コンペティションは2021年2月10日まで開催しており、まだまだ時間はたっぷりありますのでぜひご参加ください。
前置きが長くなりましたが、以下の手順で機械学習で音声を扱う方法について説明していきます。
1. そもそもニューラルネットワークではどのような形式のデータで学習しているか?
2. 音声データとは?
3. ニューラルネットワークで音声データを扱うためのアプローチ
そもそもニューラルネットワークではどのような形式のデータで学習しているか?
CNNで画像分類を行うといった処理を例にとって説明します。CNNを使って画像分類を行うときは、pngやjpegなどの画像情報をtensor型に変換すればそれをそのままinputとして学習を行うことが可能です。以下に、MNISTとCIFAR10を例にとってCNNにinputする際のデータの形をみていきます。
* MNISTの場合のinput情報
* 色 (白黒の濃淡) 1
* 縦のピクセル数 28
* 横のピクセル数 28
* CIFAR10の場合のinput情報
* 色 (Red, Green, Blue) 3
* 縦 32
* 横 32
このように、画像は色、縦、横の情報を持っておりカラーか白黒か、ピクセルの大きさによってデータのサイズが決まります。
つづいて音声のデータをニューラルネットワークにinputする方法について確認していきたいと思いますが、ここで音声データがどのような形式になっているか確認してみましょう。
音声データとは?
画像データは、白黒もしくはRGBのチャネルに輝度がデータとして格納されているようなデータ形式でしたが、音声データは時間と波の情報を持っております。ファイルフォーマットは.wavもしくは.mp3となっているのをよく見かけます。ちなみに、Nishikaのコンペでは訓練用データをmp3形式で配布しております。
音声データを可視化するとどうなるのか、訓練用音源であるモーツァルトの『きらきら星変奏曲, K. 265』 529.mp3を確認してみましょう。
librosaというライブラリを使用して可視化を行います。このライブラリは音声の読み込み、再生などの基本的な操作から前処理まで便利なメソッドが充実しているため非常に便利です。
import os
import numpy as np
import pandas as pd
import librosa
import librosa.display
import matplotlib.pyplot as plt
import glob
import IPython.display
from IPython.display import display
chrd_path = glob.glob('./data/chord/*')
piano_path = glob.glob('./data/piano/*')
violin_path = glob.glob('./data/violin/*')
data, sr = librosa.load("./data/529.mp3", sr=44100)
librosa.display.waveplot(data, sr=sr)
横軸 : 時間
縦軸 : 振幅
横軸の大きさは音源の長さと、サンプリングレートによって決まります。
サンプリングレートとは1秒間に何回、アナログ音源をデジタルに変換したかを表す数であり、CDの場合は44,100Hzとなります。この数字が大きいほうがもとのアナログ音源からの情報を損なわずにすみ、近年のハイレゾ音源にもなるとサンプリングレートが192000Hzのものもあります。
画像データは(チャネル、 縦、 横)という箱の中に輝度が格納されているというデータ形式でしたが、音声では(サンプリング数)の箱の中に振幅が格納されているというデータ形式になります。
ここで、『きらきら星変奏曲, K. 265』のデータの大きさを確認してみます。確認は以下のコードで行い、サンプリングレートと音源の長さがサンプリング数に依存するという関係性も合わせて確認してみます。
duration = librosa.get_duration(y=data, sr=sr)
print(f'サンプリングレート :{sr}' )
print(f'読み込む音源の長さ :{duration}秒')
print(f'データの大きさ :{data.shape}')
print(f'【検算】 データの大きさ=サンプリングレート x 読み込む音源の長さ {duration*sr}' )ニューラルネットワークで音声データを扱うためのアプローチ
音声データの中身がどのようになっているか確認できましたが、上記例の音源データを加工せずそのままニューラルネットワークのinputにしようとすると、shapeが非常に大きくなってしまいます。ここまで大きいデータをそのまま計算するのは高機能のマシンでないと厳しく、Google Colab(無償版)で実際に演算を行ってみるとRAMを使い果たしてセッションがクラッシュします。ですのでなるべくinputさせるデータを小さくする工夫が必要になり尚且、なるべく元のデータの特徴を損なわないような手段を取る必要があります。今回の作曲家を分類するというタスクに関して言うと、曲長やテンポといった音楽としての特徴を損なわないようにダウンサンプリングします。
音楽としての特徴を損なわずに情報をカットする手段として、高周波数をカットするという手法があります。これは人間の耳は高周波数になると音の高さの違いを区別できない性質があるため音楽としては必要ない情報であるためです。
ここからは説明簡略化のために、ピアノで「ド」の鍵盤を叩いたとき音源を例にとって解説していきます。
「ピアノのド」の音源を聞きたい人はここをクリックしてください
path = piano_path[0]
data, sr = librosa.load(path, sr=44100)
display(IPython.display.Audio(data, rate=sr))
librosa.display.waveplot(data, sr=sr)
高周波数をカットする
音楽としての特徴を損なわないようにダウンサンプリングする方法として、人間には聞き取れない高周波数領域をカットするという方針を取ります。ただ音源を読み込んだだけですと、周波数ごとの振幅の強さを得ることができず、高周波数のみをカットするのは困難です。ですので波形を周波数ごとに分解できるフーリエ変換を行っていきます。
音源1曲を丸ごとそのままフーリエ変換にかけると周波数分化能が小さくなるという性質があるため、細かい時間で区切ってフーリエ変換を繰り返すSTFT(Short time Fourier transform)を行って周波数毎に分解します。 STFTのイメージは以下の画像がわかりやすいです。
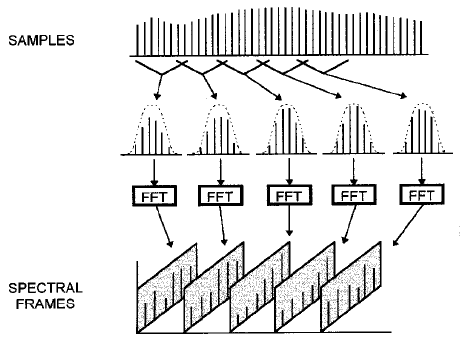
引用 : RAJMIL FISCHMAN 『The phase vocoder: theory and practice』
上記で読み込んだドの波形をlibrosaライブラリのstftメソッドを用いて、STFTにかけてみます。
以下の処理ではSTFTをかけた後に二乗をして、パワースペクトルというものを得てその後に、dB変換を行っております。
パワースペクトルは周波数ごとの振幅の強さを表しており、dB変換は振幅の強さのスケールを変換する処理です。振幅は通常10倍、100倍といったレベルで変化するため、常用対数で変換すると扱いやすくなります。常用対数で変換を行った尺度をdB(デシベル)といいます。STFTにかけた図をスペクトログラムといいます
D = librosa.stft(data)
D_2 = np.abs(D)**2
Sdb = librosa.power_to_db(D_2)
librosa.display.specshow(Sdb, sr=sr, x_axis='time', y_axis='log')
横軸 : 時間
縦軸 : 周波数
奥行き(色の濃さ) : 信号成分の強さ
基音と倍音
ドの周波数は261.6Hzであり、ピアノのドの音はこの周波数が色濃くなっていることが上のスペクトログラムからわかります。しかしそれ以外にも色濃くなっている周波数が複数存在することが上記のスペクトログラムから確認できます。
これは倍音といい、色が濃くなっている場所は261.6の整数倍である523.2, 784.8, 1046.4といった周波数です。261.6Hzは基音といい人間が感じる音の高さの周波数です。
ピアノだけでなくギターやフルートなどの他の楽器でドの音を奏でたときも同様に倍音が現れます。楽器としての音色は、この倍音の強弱によって決まるらしいです。逆に倍音を一切カットして、261.6Hzだけのsin波の音はラジオの時報のような機械的な音になります。
ヴァイオリンのドの音もスペクトログラムを確認してみると以下のようになります。
基音と倍音に対応する周波数が強く現れていることはピアノと一致しておりますが、ヴァイオリンのほうがより高周波数の倍音が強く出ているように見えます。楽器による音の違いは基音と倍音のバランスに現れるということが確認できましたね。
「バイオリンのド」の音源を聞きたい人はここをクリックしてください

スペクトログラムのイメージをもっと深めてもらうために、ド・レ・ミ・ファ・ソ・ラ・シをそれぞれ確認してみます。基音となる周波数は以下のとおりでありそこに対応した箇所が最も色濃くなっていることがわかります。
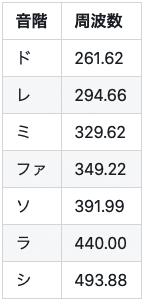

これらのスペクトログラムを得るためのコードは以下になります。
for i in range(len(piano_path)):
path = piano_path[i]
data, sr = librosa.load(path, sr=44100)
#display(IPython.display.Audio(data, rate=sr))
mpl_collection = librosa.display.waveplot(data, sr=sr)
D = librosa.stft(data)
D_2 = np.abs(D)**2
Sdb = librosa.power_to_db(D_2)
librosa.display.specshow(Sdb, y_axis='log', x_axis='time', sr=sr)
plt.show()続いて複数の鍵盤を同時に叩いた音源のスペクトログラムを確認してみます。色が濃くなっている周波数が複数にまたがっていることが確認できます。

このスペクトログラムを得るためのコードです。
for i in range(len(chrd_path)):
data, sr = librosa.load(chrd_path[i], sr=44100)
#display(IPython.display.Audio(data, rate=sr))
mpl_collection = librosa.display.waveplot(data, sr=sr)
D = librosa.stft(data)
D_2 = np.abs(D)**2
Sdb = librosa.power_to_db(D_2)
librosa.display.specshow(Sdb, y_axis='log', x_axis='time', sr=sr)
plt.show()メル周波数
人間の音高知覚についてはわかっていないところも多いそうですが、可聴域の下限に近い音は高め上限に近い音は低めに聞こえるという特性を持っております。例を上げると、1000Hzの音は500Hzの2倍の高さに感じますが、2000Hzの音は1000Hzの2倍の高さには感じないという特性です。実際には約3500Hzになると、1000Hzの音の2倍の高さに感じるようになります。このように下限に近い音のほうが周波数の変化に対し敏感に知覚できるので、上限に近い高周波数に対してスケール変換を行う必要があります。
スペクトログラムをメル尺度変換したものをメルスペクトログラムといい、librosaライブラリにはメルスペクトログラムを得るためのメソッドが用意されております。※振幅のdB変換はなされていないためdBスケールに変換する必要があります。
「ピアノのド」のメルスペクトログラムを得るためのコードです。
data, sr = librosa.load(piano_path[0], sr=44100)
mel = librosa.feature.melspectrogram(y=data, sr=sr)
log_mel = librosa.power_to_db(mel)
librosa.display.specshow(log_mel, y_axis='mel', x_axis='time', sr=sr)
スペクトログラムをメル尺度に変換することによって、周波数分解能が小さくなりshapeも小さくなります。
スペクトログラムとメルスペクトログラムのshapeの違いを確認するためのコードです。
D = librosa.stft(data)
D_2 = np.abs(D)**2
Sdb = librosa.power_to_db(D_2)
data, sr = librosa.load(piano_path[0], sr=44100)
mel = librosa.feature.melspectrogram(y=data, sr=sr)
log_mel = librosa.power_to_db(mel)
print(Sdb.shape)
print(log_mel.shape)ここまでは、例として1秒程度の単純な音源を可視化しておりましたが、もともと解析を行いたかったクラシック音源『きらきら星変奏曲, K. 265』のメルスペクトログラムを以下のコードで可視化してみます。
data, sr = librosa.load("./data/529.mp3", sr=44100)
print(data.shape)
librosa.display.waveplot(data, sr=sr)
plt.show()
mel = librosa.feature.melspectrogram(y=data, sr=sr)
log_mel = librosa.power_to_db(mel)
librosa.display.specshow(log_mel, y_axis='mel', x_axis='time', sr=sr)
print(log_mel.shape)
もともとは、音楽の特徴を損なわないようにしつつデータを小さくするというモチベーションでしたので、もとの音源とメルスペクトログラムに変換したときとのデータのサイズ(shape)を確認してみます。
生音源shape (16122240,)
・16122240はサンプリング数であり振幅値が格納されている
メルスペクトログラムshape (128, 31489) = 4030592
・縦軸 128 : 周波数分解能
・横軸 31489 : サンプリング数
もとの生音源データから約1/4程度に下がっていることが確認できました。しかしまだNNにinputするにはサイズが大きいので、ここからサンプリングレートを下げたり、stftを行うステップ数を変更することによってさらにサイズを小さくしていきます。
これらを変更するためのパラメータは以下のlibrosaの公式ドキュメントをご確認ください。
librosaのドキュメントはここをクリックして確認してください
ためしに以下のコードで、サンプリングレートを16000、stftを行うステップ数を2048(※デフォルトでは512)に変更したときのshapeを確認してみますと(128, 2857)までサイズを落とすことができました。しかしサンプリング数を小さくしているということは単純に情報量を小さくしているだけですので、機械学習の精度を下げる可能性もあることに注意が必要です。
data, sr = librosa.load("./data/529.mp3", sr=16000)
mel = librosa.feature.melspectrogram(y=data, sr=sr , hop_length=2048)
log_mel = librosa.power_to_db(mel)
print(log_mel.shape)
librosa.display.specshow(log_mel, y_axis='mel', x_axis='time', sr=sr)
上記の手順でメルスペクトログラムを得ましたが、これは見方によっては画像として捉えることも可能です。画像は縦横に輝度が格納されておりましたが、音声では縦横に振幅の強さが格納されているといった度合いです。ですのでメルスペクトログラムは画像と同じようにニューラルネットワークで学習することが可能となります。非常に長くなってしましましたが、機械学習で音声を扱う方法についてはこれで解説を終わりたいと思います。
さいごに
音声解析の勉強を実際に手を動かしながら学習しようととすると訓練用のデータを集めて、上記の前処理を行って、学習モデルを作ってトレーニングして、いいモデルが出来上がったか確認するためにテストする。といった非常に長い道のりになります。
クラシック音楽の作曲家分類のコンペティションページでは音源を無料でダウンロードすることができさらに前処理、トレーニングに関するコードが公開されております。作曲家の特徴を見つけ出すというタスクは非常に興味深いテーマですので飽きずに音声解析について学べるコンテンツなのではないかと思ってます。Nishikaはコンペティションの場を提供しておりますが、勉強がてらにもお気軽にご参加いただければと思います。
この記事が気に入ったらサポートをしてみませんか?

