
ビンゴゲームと信頼性のあるプログラムの書き方
この記事はpaiza Advent Calendar 2021の17日目及びPython Advent Calendar 2021の15日目(空いてたので)の記事になります。
ネタに迷いましたが、ビンゴゲームのシミュレータプログラムがなぜか手元にあったので、これを整理して投稿することにしました。
記事の目的
ビンゴゲームの当選確率分布を求めます
最短でビンゴに当選することがどれくらいあり得ないでしょうか?
プログラムを楽に書く方法を考えます
楽なプログラムは信頼性が高いです
楽なプログラムは拡張しやすいです
楽なプログラムはユニットテストに使えます
このシミュレータは信頼できるのかを詰めます
ビンゴとは
おそらくビンゴを知らない人はいないんじゃないかと思いますが改めてビンゴとは何かを定義してみます。
ビンゴ参加者は5行5列計25マスからなる(ビンゴ)カードが配られる
カードの中央マスにはfreeと書かれていてビンゴ参加者は最初にこれを「開ける」
カードの中央マス以外には(普通は1~75の)数字が書かれている
ビンゴ主催者は(普通は1~75の)数字を読み上げる
ビンゴ参加者は読み上げられた数字がカードにあるか探し、あればその数字の場所を「開ける」
ビンゴ参加者はカードを見て、「ビンゴ」が成立していないかを確認する
「ビンゴ」とは、縦または横またはななめの連続する5つの数字を「開けた」ことと定義します。ビンゴを成立させるためのラインは縦5本横5本ななめ2本計12本存在します。
4から6をゲームが終わるまで繰り返す
参加者は一人でも(たぶん)ビンゴとしては成立しますし、2回ビンゴしても意味があったり、連続する4つの数字を「開けた」ことを「リーチ」と呼ぶなどいろいろルールはありますが、だいたい1-7で示した手順がビンゴの重要な部分でしょう。
ビンゴ確率シミュレータ
今回はビンゴが成立するまでの読み上げ回数の確率分布を求めるプログラムを書きました。所要時間は2~3時間ぐらいです。
paizaランクでいうとランクB〜Aの間ぐらいの難易度ではないかなと思います。上述のルールをもとに正確なシミュレータがラクに書ける人はpaizaでBランク(かAランク)が取れると思いますので、ぜひスキルチェックで力試ししてみましょう。
まずは全体のソースコードをベタ貼りして、後で解説を加えていきます。
import math
import random
from collections import Counter
MAX_NUMBER_OF_BINGO = 75
NUMBERS = range(1, MAX_NUMBER_OF_BINGO+1) # 1~75までの数字
def formula_accum_prob(n): # 累積確率分布を数式で計算
a = math.perm(n, 5) / math.perm(MAX_NUMBER_OF_BINGO, 5)
b = math.perm(n, 4) / math.perm(MAX_NUMBER_OF_BINGO, 4)
return 1-(1-a) ** 8 * (1-b) ** 4
def formula_prob(n): # 確率分布を数式で計算
return formula_accum_prob(n) - formula_accum_prob(n-1)
def generate_board(): # 5x5のビンゴボード生成、真ん中はfree(0で表現)
numbers_on_board = random.sample(NUMBERS, k=24)
board_1d = [*numbers_on_board[:12], 0, *numbers_on_board[12:]]
return [board_1d[5*i:5*(i+1)] for i in range(5)]
def bingo_patterns(board): # ビンゴが成立する5つの数字の組 (全部で12組)
return frozenset([
*[frozenset(board[i]) for i in range(5)], # 横方向5列
*[frozenset([board[i][j] for i in range(5)]) for j in range(5)], # 縦方向5列
frozenset(board[i][i] for i in range(5)), # 右下ななめ
frozenset(board[i][4-i] for i in range(5)) # 左下ななめ
])
def select(): # 最初はfreeが開く、その後は1~75までをランダムに抽出
return [0, *random.sample(NUMBERS, k=MAX_NUMBER_OF_BINGO)]
def picks_to_bingo(): # ビンゴが成立するまでの読み上げ回数
board = generate_board() # ビンゴカード作成
patterns = bingo_patterns(board) # ビンゴパターン構築
selected_numbers = select() # 主催者が読み上げた数字の列
for i in range(0, MAX_NUMBER_OF_BINGO+1): # i回目までに読み上げられた数の組
choice = set(selected_numbers[:i+1]) #
lines = [pat.intersection(choice) for pat in patterns]
max_lines = max([len(line) for line in lines])
if max_lines == 5:
return i
return MAX_NUMBER_OF_BINGO
def sample_probs(number_of_trial): # 読み上げ回数の確率分布
counts = [picks_to_bingo() for _ in range(number_of_trial)]
counter = Counter(counts)
return {k: v/number_of_trial for k, v in sorted(list(counter.items()))}
def plot_to_png(by_formula, by_sample1, by_sample2): # グラフ描く
import matplotlib.pyplot as plt
(xs_formula, ys_formula) = zip(*by_formula.items())
(xs_sample1, ys_sample1) = zip(*by_sample1.items())
(xs_sample2, ys_sample2) = zip(*by_sample2.items())
plt.plot(xs_formula, ys_formula, label="formula")
plt.plot(xs_sample1, ys_sample1, label="sample10000")
plt.plot(xs_sample2, ys_sample2, label="sample1000000")
plt.legend()
plt.savefig(f"bingo_{MAX_NUMBER_OF_BINGO}.png")
if __name__ == "__main__":
by_formula = {k: formula_prob(k) for k in range(4, MAX_NUMBER_OF_BINGO+1)} # 数式利用
by_sample_10000 = sample_probs(number_of_trial=10000) # 10000回ビンゴゲームする
by_sample_1000000 = sample_probs(number_of_trial=1000000) # 1000000回ビンゴゲームする
print(by_formula)
print(by_sample_10000)
print(by_sample_1000000)
plot_to_png(by_formula, by_sample_10000, by_sample_1000000)paiza.ioでの実行結果(時間制限などがあるので縮小版です)
参考文献としてビンゴの確率の数式を提示しているサイトがありましたので、こちらの数式を拝借しformula_probとして実装しています。
実行結果をプロットしたのが以下のグラフです。

横軸は読み上げた数字の数、縦軸はビンゴになる確率です。例えば主催者が40個数字を読み上げたタイミングで、ビンゴになる確率がだいたい0.04 = 4%ということになります。
最短でビンゴに到達するのは主催者が4個数字を読み上げた時ですが、数式に基づくと100万回ビンゴゲームをやって3回起きる程度です。実際にシミュレータを動かすとその感覚は正しく、標本での確率が0になってしまうこともあります。誰もが最短でビンゴすることに憧れますが、その確率は宝くじと結構いい勝負ができてしまうぐらい難しいようです。(宝くじの1等は1/2000万なので60倍簡単ではありますが)
このプログラムは信頼できるか?
さて上のシミュレータは正しい実装なのでしょうか?なにやら数式の結果と少しずれています。数式の結果だと4%を超えているところがあるのに、シミュレータの結果は4%を超えていません。数式が正しいのか、シミュレータが正しいのか。どっちが正しいかわからない、世の中そんなことばかりです。
他の人のシミュレーション結果をカンニングするとやはり4%を超えていないので、この実装は一旦は大丈夫そうに見えます。
https://techracho.bpsinc.jp/nozue/2016_12_13/30804
http://www.din.or.jp/~take_din/math/BINGO2.html
ボトムアッププログラミング
信頼できる大きなプログラムに書くための手法があります。信頼できる小さなプログラムピースをレゴのように組み立てて、より大きなプログラムを実装していく手法で、ボトムアッププログラミングと呼ばれています。この考え方を今回のビンゴシミュレータを用いて解説しましょう。
ビンゴゲームをシミュレーションするには、まずビンゴカードが絶対に必要です。ならビンゴカードを作る小さなプログラムを書きましょう。
MAX_NUMBER_OF_BINGO = 75
NUMBERS = range(1, MAX_NUMBER_OF_BINGO+1) # 1~75までの数字
def generate_board(): # 5x5のビンゴボード生成、真ん中はfree(0で表現)
numbers_on_board = random.sample(NUMBERS, k=24)
board_1d = [*numbers_on_board[:12], 0, *numbers_on_board[12:]]
return [board_1d[5*i:5*(i+1)] for i in range(5)]実装はややテクニカルですがやりたいことは簡単で、1~75の数字のうち24個の数字を選んで、ビンゴボードに割り当てています。(0はfreeを表します。)より細かい説明をすると、[12個の数字, free, 12個の数字]という数列(board_1d)をまず作り、それを5つの数字ごとに行を分ける処理をしているだけです。
プログラムが書けなくても下の実行リンクを押せば、「はいはいボードができてるね」とわかることでしょう。
ここから先は実装スタイルによりますが、ビンゴを成立させるための12本のラインを表現することにします。なぜこれに着目するかというとビンゴのラインそのものはカードが決まれば不変であるからです。
不変量あるいは不変な関係に着目するのはプログラムの柔軟性と信頼性を両立する上で重要なことだと思います。(物理とかでもエネルギーとか角速度とか運動量とか不変量に着目しますが、そういうものに立脚したルールは壊れにくいです。不変な仕様を見出せばコードを書き換える必要がないので、リファクタリングと呼ばれる書き換えの必要性そのものをなくします。
ルール実現に必ずしも必要でない人為的な可変状態を追加することで、高速化できたりいろんな機能を実現できますが、それを極力留保するのがボトムアッププログラマの技だと言えます。
def bingo_patterns(board): # ビンゴが成立する5つの数字の組 (全部で12組)
return frozenset([
*[frozenset(board[i]) for i in range(5)], # 横方向5行
*[frozenset([board[i][j] for i in range(5)]) for j in range(5)], # 縦方向5列
frozenset(board[i][i] for i in range(5)), # 右下ななめ
frozenset(board[i][4-i] for i in range(5)) # 左下ななめ
])これまた実装はややテクニカルですがやりたいことは簡単で、横5行、縦5列、ななめ2本計12本のラインにある数字の組を列挙した形になります。frozensetってなんだという感じですが、{12,44,60,65,75} みたいな組み合わせが12組存在して、組み合わせの中にある数字が全て読み上げられるとビンゴが成立するという状態になります。
ビンゴのパターンは明らかにどのようなビンゴカードが配られたかに依存します。だからboardが関数の入力として入ってくるのが自然だと言えます。
下の実行リンクを押せば、どういうものかわかります。frozensetを使っているせいで少し読み取りにくいですが、5つの数字が12組あり、5つの数字が全部読み上げられるとビンゴになるとわかります。
またルールを見ると主催者が数字を読み上げるとあります。これを表現する小さなプログラムを構築します。
def select(): # 最初はfreeが開く、その後は1~75までをランダムに抽出
return [0, *random.sample(NUMBERS, k=MAX_NUMBER_OF_BINGO)]主催者は一番最初に0(free)と読み上げることはないですが、そうした方が処理が楽になるため工夫しています。その後は75個の数字をランダムに読み上げるという想定で、読み上げた数字を数列として表現します。実際にはゲームが終わったら主催者は数字の読み上げをやめますが、リアルさは一旦棚上げしました。
ここまでで、ビンゴのルールに必要なものは大体用意できたので、後はビンゴゲームを実際に動かすプログラムを書くだけで終わります。
def picks_to_bingo(): # ビンゴが成立するまでの読み上げ回数
board = generate_board() # ビンゴカード作成
patterns = bingo_patterns(board) # ビンゴパターン構築
selected_numbers = select() # 主催者が読み上げた数字の列
for i in range(0, MAX_NUMBER_OF_BINGO+1): # 数字の読み上げ回数
choice = set(selected_numbers[:i+1]) # i回目までに読み上げられた数の組
lines = [pat.intersection(choice) for pat in patterns] # ビンゴパターンかつ「開いた」数字
max_lines = max([len(line) for line in lines])
if max_lines == 5:
return i
return MAX_NUMBER_OF_BINGOこれがビンゴのコアなので少し複雑ですが、ピースをうまく組み合わせているので10行にも満たないコードです。ビンゴカードをランダムに生成し、そのカードのビンゴパターンを構築し、主催が読み上げた数字列を生成してセットアップします。
後は主催が読み上げを開始したと想定します。例えばi=5なら、0(free)とランダムな数字を5つ読み上げた状態だと考えます。この状態で12個のビンゴパターンのそれぞれについて、何個の数字が「開いた」かを調べ、その最大の数が5の場合はビンゴが成立しているので、ビンゴが成立した時の読み上げ回数を返しています。75個の数字を全部読み上げれば必ずビンゴは成立しているはずなので、その場合は75を返します。この数字を集めることで確率分布が得られます。
さてここまで読めばわかるかと思いますが、ボトムアッププログラミングにおけるピースは関数です。関数を責務分割のための基本ピースだと考えることが重要で、そう考えることで自然にプログラムをルールとその不変量に着目して書き下すことができます。関数を軸に考えることで可変状態の介入余地を最小化できます。(もちろん可変状態が必要ならば利用しましょう。)
また関数やコレクションは概ねどのような言語でもサポートしている機能なので移植も簡単です。
ルールを直接的に書き下す利点
今回の実装では、あまり複雑なトリックを使わずに、極力ビンゴのルール(仕様)に沿って処理を実現しました。この方法だと一回の読み上げごとに、12回の計算が走ったり、正直なところ無駄な処理が多いです。このように実装するメリットはあるのでしょうか?
一番のメリットはテストが簡単で手が抜けるということです。このシミュレータを書くのにせいぜい2時間程度でしたが、一つ一つのピースが検証しやすいのでそこそこ信頼できるコードになっています。
ルールを直接的に書き下したということは、ルールを書き換えても追従させることが簡単だということです。例えば
ビンゴではなくリーチの確率を求めたい→if max_lines == 5:を4に書き換える
ダブルビンゴの確率を求めたい→max_linesあたりを書き換えてビンゴの数を取れるように書き換える
複数人でプレイした場合にプレゼントをもらえる確率分布を求めたい→できるはずなので頑張ってください
期待値を求めるのは簡単ですが、分散や確率分布を求めるのはシミュレータがあると助かります。解析的に求められる人がいればこのようなシミュレータは不要でしょう。
ビンゴの最大数字を75から25に変えるとドラクエ8のカジノに出てくるビンゴがシミュレートできるので攻略が捗ります。
上記の実装だとカードサイズの変更には対応していないですが、そうした変更があってもピースを一つずつ修正していくことで信頼性を保ちつつプログラムを変更させることが簡単になります。
他のメリットはこれを叩き台としてより高速な実装へと移行できることです。不変量に基づくプログラムでは高速化の限界があり、より細やかな状態管理を必要とすることが多いですが、そうした複雑なプログラムの正しさを検証するのは簡単ではないです。そうしたものを作る時においても基準実装として利用し、例えばユニットテストに応用することができます。
ビンゴゲームのさらなる解析
ここまではボトムアッププログラミングについての話でした。ただ一つ心残りなことがあります。
なぜ数式とシミュレータの結果がずれるのだろう?本当にシミュレータは正確か?
正直ここら辺の厄介ごとからはトンズラしたかったですが、結論を出さないと寝るにも寝られない感じになりました。理論と現実の差を埋める継続的努力こそがおそらく工学(エンジニアリング)と呼ばれるものなのです。
正確な確率を求めるには?
│
├ 1.頑張って数学を勉強して解析式を導き出す。
│
│ [まちがい]
│ 確実な方法ではありますが、時間がかかるのが難点です。
│ それよりも別の手段を探してみませんか?
│ ちょっとした競プロ技術でなんとかなるかも?
│ ↑
│ ココがポイント!
│
└ 2.全探索を使う
[せいかい]まず解析式を立式をすることを考えましたが、数学弱者なのでそもそもそれが端的に表現可能かどうかすらわかりませんでした。
同様に確からしい組み合わせ(事象)を余さず列挙し、ビンゴのパターンを数える。それもまた確率の公理に根ざした数学と言えるでしょう。
5×5のカードを見ながらこの本質を捉えることは難しいので3×3のカードを考えます。本来であればカードに描かれる数字はランダムですが、数字を固定化しても対称性は失われないと考えられるので以下のようなカードのことを考えます。
| 1 | 2 | 3 |
| 4 | 0 | 5 |
| 6 | 7 | 8 |読み上げの最大数を8とすれば、読み上げの全パターンは8!=40320通り程度だと推察できます。(もしも5x5サイズを相手にすると24!パターンあるので計算量的に厳しい)
また2回読み上げた時のビンゴの確率だけは簡単に計算できて、4×2/8×1/7 = 1/7です。(3回も頑張れば立式できそう?)
これをもとにシミュレータ結果をプロットしました。
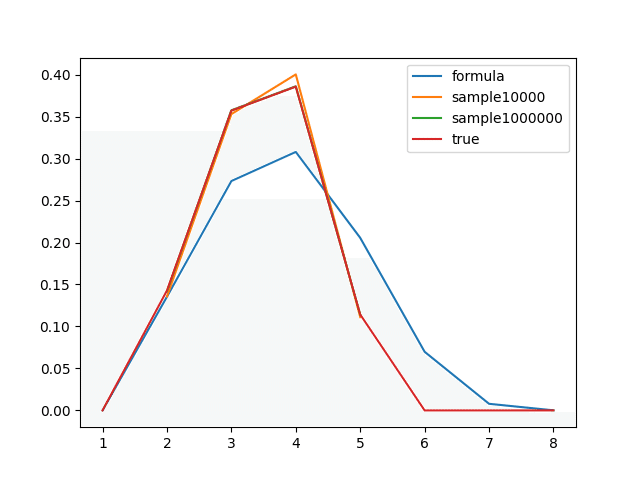
グラフから読み取りにくいですが、シミュレータと全探索結果が一致しています。3×3の場合においてシミュレータの方が正しいことがわかりました。5×5で検証できないですが、3x3の結果を通じて数式は近似式であることがわかりました。(というより「位置を考慮しない」と元記事に書いてあります、そしてその含意は私の数力では理解できていません。)
結論
当選確率分布が求まりました
どうやらシミュレータは正しそうです
ボトムアッププログラミングで信頼性の高いプログラムを書けます
シミュレータ書くより記事と考察書くのに時間がかかりました
この記事が気に入ったらサポートをしてみませんか?
