
国語の数学【1】 対立概念を因数分解する
自分は、大学時代は理系で工学部、そのあと、コピーライターになりました。
つい言葉を考えるときも、理系的に考えてしまうのですが、国語を数学的に考える、ということは、あまり行われてないのではないか、と思い、noteで思考の実験をしてみることにしました。
数学の用語もざっくりした感じで話で進めます。間違っているところがあったら、すいません。(ちゃんと調べれば、こういうことを研究している人もいるかもしれません。いたら、ぜひ教えてください。)
初回は、「対立概念を因数分解する」です。
ここでいう対立概念とは、「二律背反」と呼ばれるもの。一方を大事にすると、もう一方が犠牲になる、というものです。
ビジネスの世界でも、デザインの世界でも、対立概念はよく現れます。結果、折り合いをつける、双方痛み分け、バランスを取る、といったことが行われているわけです。
たとえば、こんな対立概念の因数分解を試みます。
シンプル←→複雑
とても多く現れる対立概念です。

シンプルなもの・・・要素の数と種類が少ない
複雑なもの・・・要素の数と種類が多い
この状態では、二律背反、両方を満たすことは不可能です。
次に、この両方を満たしているものはないか、と考えてみます。(この思考実験において大事なプロセスです)
シンプルなおかつ複雑なものの例

規則性があるものを、人はシンプルと感じます。
シンプルと複雑には、数や種類の量だけが絡んでいるわけではなく、規則性のありなし、も関係しています。
規則性があると、人は、なぜシンプルに感じるのか。
それは、「脳が楽、だから」ではないでしょうか。

ここで、シンプル←→複雑 は、以下の2つに因数分解できることがわかります。(もしかすると、もっと別の因数分解もあるかもしれませんが)
シンプル・・・脳への負担が少ない
複雑・・・脳への負担が多い
シンプル・・・数と種類が少ないもの
複雑・・・数と種類が多いもの
「シンプルなのに複雑な問題だ」・・・数と種類は少ないのに、脳への負担が大きい。

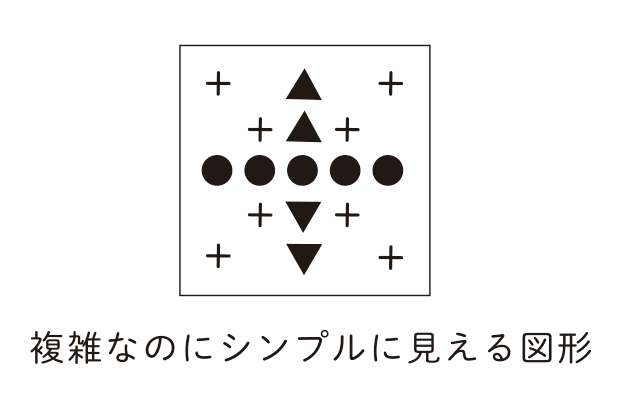
「複雑なのにシンプルに見える図形」・・・数と種類は多いのに、脳への負担が少ない。
シンプル←→複雑
を、
脳への負担小←→脳への負担大
数と種類小←→数と種類大
この2つの対立概念に因数分解すると、解決できることがありそうです。
これが、対立概念を因数分解する基本的な方法になります。
他にも、
優しい←→冷たい
を因数分解してみると、
反応が丁寧←→反応があまりない
相手のことを考えている←→相手のことを考えていない
に因数分解できそうです。
冷たそうなのに優しい人
=反応はあまりないのに、相手のことを考えている人
優しそうなのに冷たい人
=反応は丁寧なのに、相手のことを考えていない人
という風に。
対立概念の因数分解、やってみてください。
人生の謎がいくつか解けますように。
国語の数学、気が向いたら、また書きます。
※矛盾する2つの事柄を、さらに高い段階で解決する方法のことを、アウフヘーベンと呼びますが、今回の「因数分解」という方法がアウフヘーベンと呼べるのかは分かりません。
練習問題:
硬い←→柔らかい
を因数分解してください
第2回「言葉を引き算する」はこちら。
