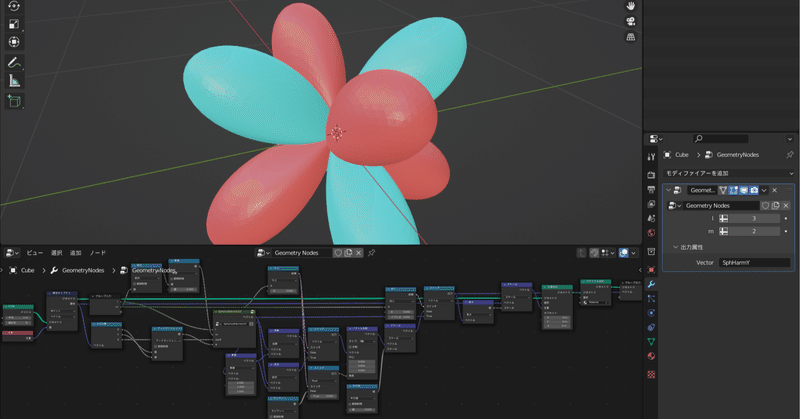
Blenderでお手軽に球面調和関数を描こう
球面調和関数を描いたこと、ありますか?
多分描いたことない人が多いと思います
私はこの記事を書くにあたって初めて描きました
球面調和関数はこういうやつです
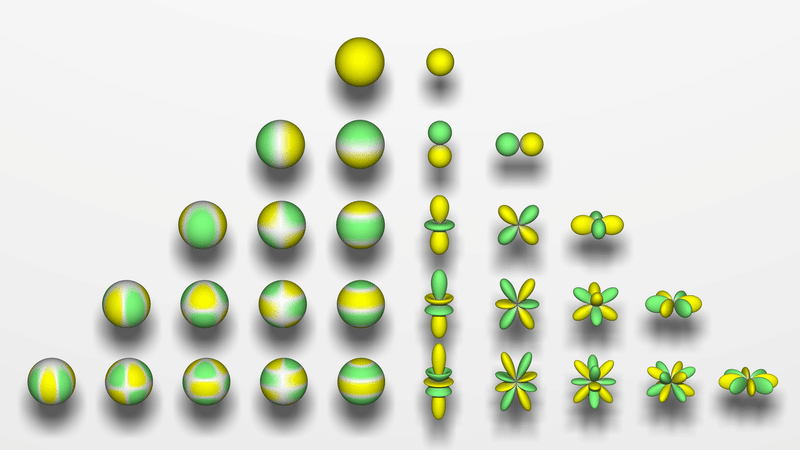
電子軌道と密接な関係があり、似たような形の図を化学の教科書などで見たことがある人もいると思います
電子軌道の模型は国立科学博物館にも展示されています
昔(2016年4月24日)に撮った国立科学博物館にある電子軌道の模型 pic.twitter.com/JFzR4FXSgS
— Melville (@MelvilleTw) February 6, 2022
おもしろい形ですよね
ところで最近、Blenderという3DCGソフトが流行っていまして、
なんとこれを使うとお手軽に球面調和関数が描けます!!
「球面調和関数は知ってるけどBlenderは触ったことない…」
「Blenderは触ってるけど球面調和関数はさっぱり…」
「球面調和関数もBlenderも知らんよ」
という人でも大丈夫、この記事を読めばあなたもBlenderで球面調和関数を描けるようになります!
追記 :
…という記事のつもりだったのですが、実際に書いてみたところ記事がめちゃくちゃ長くなってしまいました…
でもこの記事の縦幅の半分ぐらいは画像かGIFが占めていますし、一歩一歩はとても簡単です!本当です!
ぜひぜひBlenderをインストールして実際に操作しながら読み進めてもらえたらと思います
この記事の最後に、ノード全図を貼ったのでうまくいかなくて困っても、
それを見て作っていただければ完成できるようになっています
目標の確認
最初にこの記事の目標を確認しておきます
球面調和関数は $${Y_l^m(θ, ϕ)}$$ と表記される関数で、$${(l, m)}$$ の値によって様々な形をみせてくれます
この記事では $${Y_l^m(θ, ϕ)}$$ の形が下の図のような形になれば成功とします
原点から $${(θ, φ)}$$ 方向に $${| Y_l^m(θ, ϕ) |}$$ の長さだけ離れた点の集合として描かれています
この図では $${Y_l^m(θ, ϕ)}$$ の値が正のときは緑、負のときは青で描いているようですね
色までこの図の通りにすることは考えませんが、色分けも行います
それでは制作に取り掛かりましょう!
Blenderをインストールする
【重要!】バージョンは必ず3.0以降を選択してください
(3.0以降の機能を使用するため)
Blenderを起動する
起動すると次の画像のようになっていると思います
この記事では日本語設定で説明していきます
Blenderのデフォルトの視点操作は
「マウス中ボタンドラッグ」で回転
「Shift + マウス中ボタンドラッグ」で平行移動
「マウススクロール」でズームインアウト
です
Geometry Nodesを扱う
今回「Geometry Nodes」という機能を使って作図を行います
画面上部の「Geometry Nodes」のタブをクリックし、
「新規」ボタンを押して新しいGeometryNodesを作成します
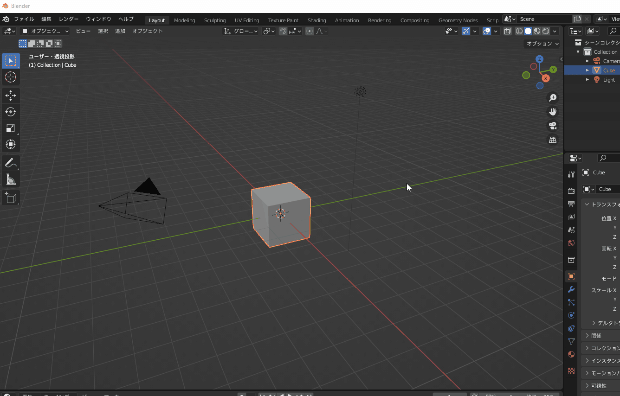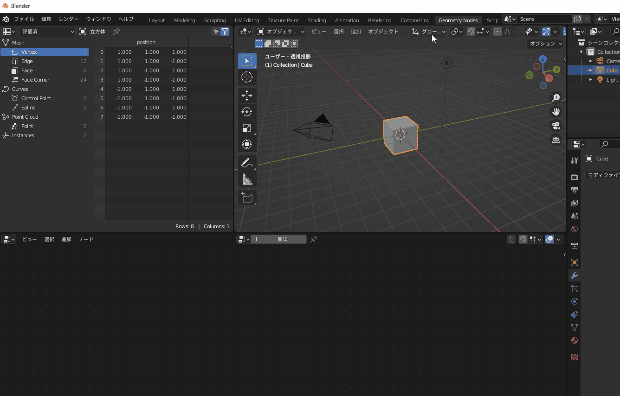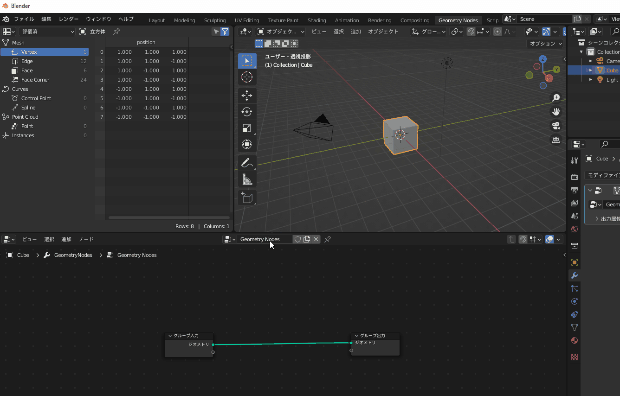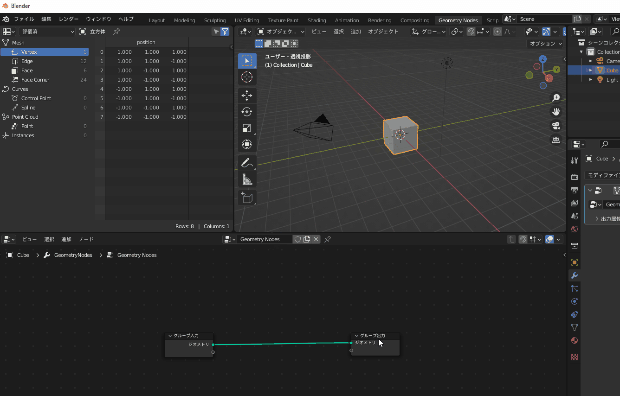

これが作られたGeometryNodesです
Geometry Nodes に触れたことがない人も多いかと思いますので、
例を見ながら理解を深めていきましょう
Geometry Nodesの作例
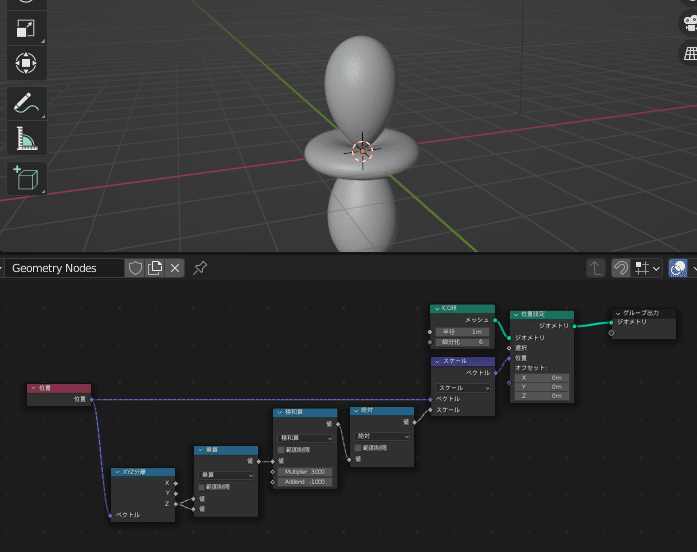
Geometry Nodesではノードと呼ばれる四角同士を適切につなぐことで3DCGの要素(頂点など)を操作することができます
例えば次の画像の例では、上のようにノードを繋げると、下のような3Dモデルが出来上がります
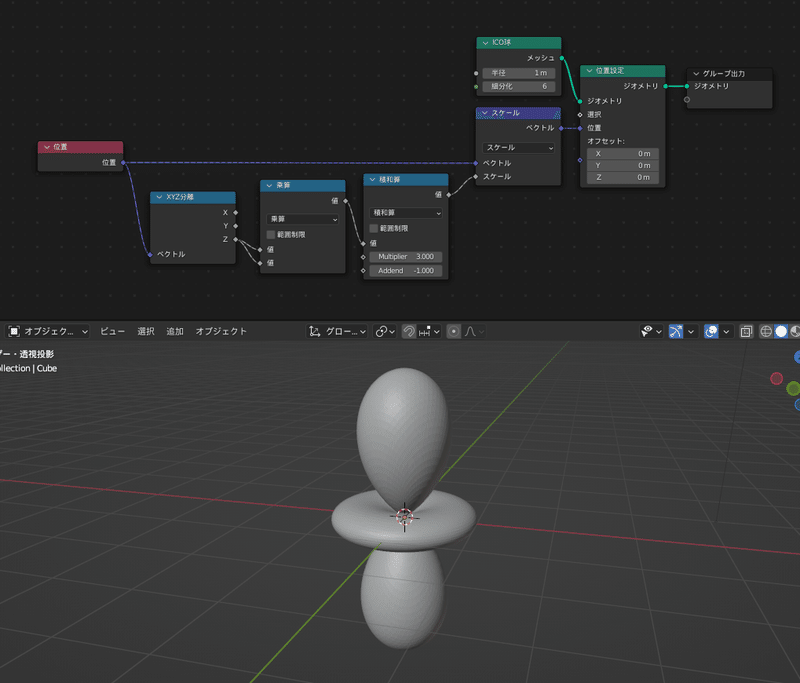
…あれ?
もう既にこれ球面調和関数 $${Y_2^0(θ, ϕ)}$$ の形ですね…?
そうです、たった8つのノードをつなげただけでこの形ができちゃうんです!
Geometry Nodesの基本
まず重要なポイントですが、Geometry Nodesは左から右へ情報が流れていきます
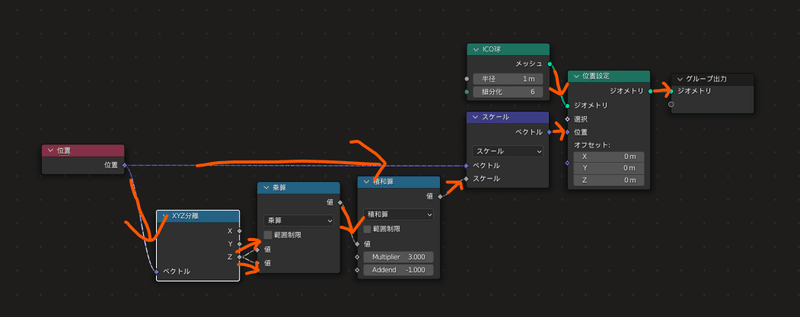
各処理を行うノードには左右に点がいくつかついていますが、
これをソケットと呼びます。
左側が入力のソケット、右側が出力のソケットになっています
よく見るとソケットはいろんな色がついていますが、これらは送られる情報の型を表しています
灰色 : 実数(float)
紫色 : ベクトル(float3つ)
暗めの緑 : 整数
ピンク : Boolean(TrueかFalseのいずれか)
鮮やかな緑 : ジオメトリ(メッシュなど)
(よく見るとソケットの形状にも丸とひし形がありますが、今は一旦気にしなくて大丈夫です。あとでまた説明します)
実際に作例を作ってみる
最低限の基本は抑えたので、さっそく作例を真似して作ってみましょう
操作説明は都度説明していきます
まず、当分先までグループ入力ノードは使わないので消します
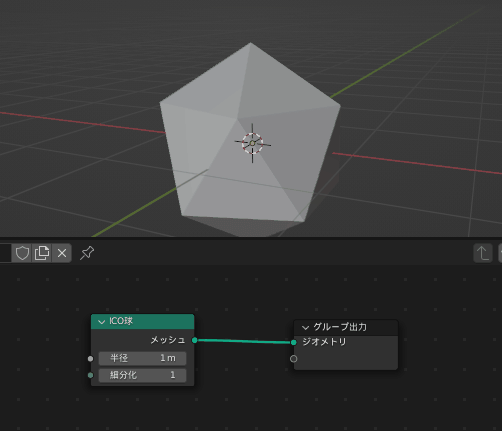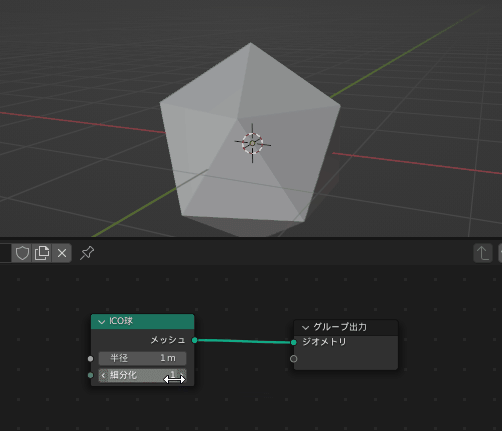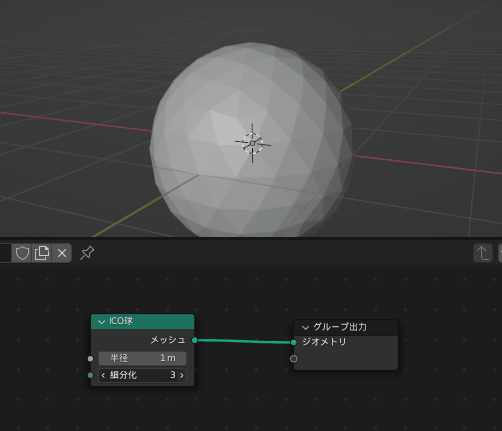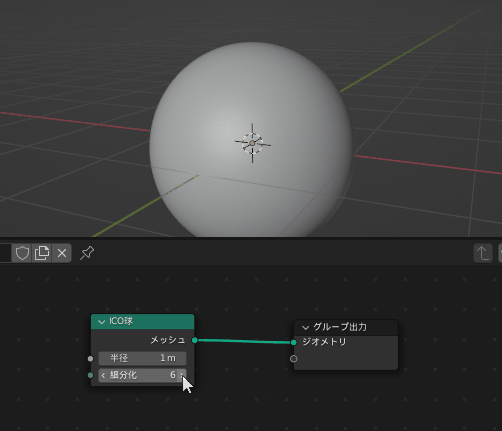
次に、「ICO球」ノードを作成してグループ出力ノードに繋ぎます。

出力ソケットから入力ソケットにドラッグ&ドロップで、線を繋ぐ
(ちなみに線を消したい場合は入力ソケットからドラッグして何もないところにドロップします)
ここまでで、画面に正二十面体が表示されていれば成功です
(なお、ICO球の「ICO」はIcosahedron(正二十面体)のことです)
ICO球ノードの「細分化」を6などに設定するとかなりなめらかな球に見えるようになります
(ところで $${Y_0^0(θ, ϕ)}$$ はただの球なので、既にひとつ球面調和関数の形が描けたとも言えますね!
ただし、実際には規格化のための定数(以後 $${N_l^m}$$ と書く)がつきます。
これは後で考慮しますが、現段階では一旦無視、すなわち $${N_l^m = 1}$$ であるものとみなして進むことにします)
次に、「位置設定」ノードを作成して、ICO球とグループ出力を繋いでいる線の上に置きます

このように、自動的にICO球とグループ出力を繋いでいる線が消え、代わりに位置設定ノードにそれぞれ繋がってくれます
位置設定ノードでは各頂点の位置を設定することができます
繋いだだけの状態では何も変化がありません
作成直後の位置設定ノードの「位置」ソケットに何も繋がってない場合は、現状の位置が入力されているのと同じことになります
つまり、次のように明示的に「位置」ノードを繋いでいる状態と全く同じです(位置ノードは、その頂点の現在の位置ベクトルを出力します)

ここでベクトルの操作をしてやると実際に頂点を動かせます
例えば「ベクトル演算」ノードを使ってスケールをかけてみましょう

「ベクトル演算」ノードによって球が拡縮されました!
このように、Geometry Nodesでは位置のベクトルをうまく処理して新しい位置を設定できるわけです
ICO球は半径が1mの球、つまり単位球ですので、ここから $${(θ, φ)}$$ を取り出して、球面調和関数 $${Y_l^m(θ, ϕ)}$$ の値をスケールに流し込んでやれば球面調和関数の可視化ができる、という算段です!
位置の三次元ベクトルから $${(x, y, z)}$$ のそれぞれの値を取り出すには、「XYZ分離」ノードを使います

これで $${x}$$ と $${y}$$ のそれぞれの二乗の和の平方根と $${z}$$ を使ってアークタンジェントとかを使えば $${θ}$$ が求まる…と思うわけですが、
よく考えるとそんな面倒なことをする必要がないことに気づきます
というのも、球面調和関数の中で $${θ}$$ は $${\cos θ}$$ か $${\sin θ}$$ の形でしか出てこず、その上 $${z =\cos θ}$$ だからです
特に、上の添字 $${m}$$ が0の場合に至っては $${\cos θ}$$ しか登場していません
つまり例えば $${Y_1^0(θ, ϕ) = N_1^0\cosθ}$$ の形をつくりたければ、取り出した $${z}$$ の値を直接スケールに流してやれば…

おっと!下半分が描画されていませんね、 $${z}$$ に絶対値をつけるのを忘れていました
(正確には描画されていないのではなく、上半分と重なっている)
絶対値をとるなどの大抵の数学的操作は「数式」ノードで取り扱うことができます(この記事で一番多く使うノードです)

無事に l=1, m=0 の球面調和関数の形が描画できた
ここまでくればあと少しで球面調和関数の形が描けます(いや、もう既に2パターン描いているのですが!)
$${Y_1^0(θ, ϕ) = N_1^0(3\cosθ^2+1)}$$ ですので、
数式ノードをもう一つ追加して、$${3z^2+1}$$ の形を作りましょう
「乗算」と「積和算」を利用します

ちなみに、積和算は乗算と加算を同時に行うノードで、
コンピュータ的には積和算も乗算も加算もコストは同じなので、
積極的に利用すると高速化できます
おめでとうございます!
これで球面調和関数 $${Y_2^0(θ, ϕ)}$$ の形が描けました!
と言いたいところですが、実は $${Y_1^0(θ, ϕ)}$$ のときと同じ誤ちをしています
今回は見た目には変化がありませんが、こだわるならちゃんと絶対値をつけましょう
色をつける
さて、ここで他の球面調和関数もやってもいいのですが、
せっかくですのでこの3Dモデルに色をつけたいと思います
色をつけるにあたって、「マテリアル」と「属性」というものを扱っていきます
マテリアルを設定する
まずマテリアルを扱うために「マテリアル設定」ノードを挟んでマテリアルを使用する宣言をします
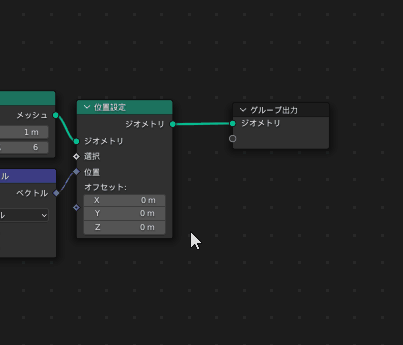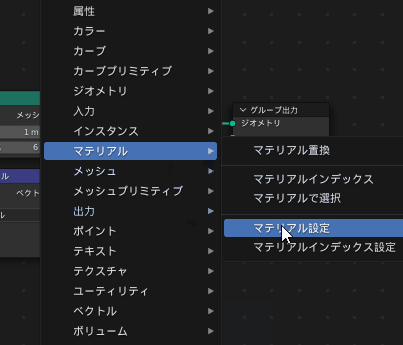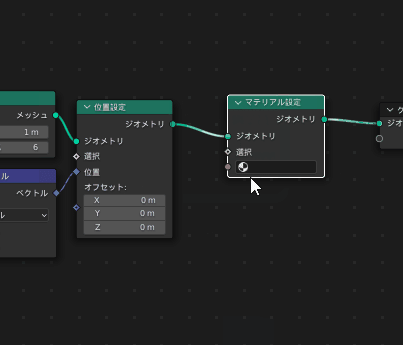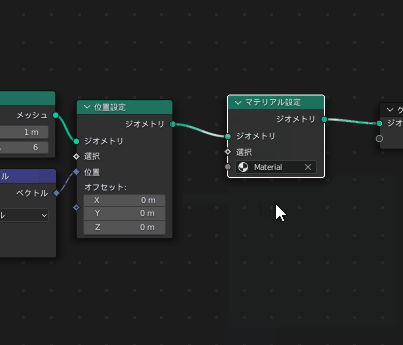
続いて、マテリアルを編集していきます
マテリアルの編集はShadingタブに切り替えて行うと便利です
Blenderではジオメトリだけではなくマテリアルもノードで扱うことができます
元から置かれているプリンシプルBSDFノードの「ベースカラー」をいじってみると、実際に色が変わるのがわかります

せっかくなので、球面調和関数の値(複素数)の偏角と色相を対応させたいと思います
色相をもとに色を作成するには「HSV合成」ノードを使います
SとVに適切な値(例えばS=1, V=1)を入力してHの値を0から1の範囲で動かすといろんな色が出力されます

S=1 でもいいですが個人的には S=0.9 ぐらいだと可愛いかなと思うのでこれでいきます
複素数の偏角を求めるには「数式」ノードの「アークタンジェント2」を使うのが良いですが、ノードが返す値は $${-π}$$ から $${π}$$ なので少し工夫する必要があります
結論としては次の画像のようにノードを繋げばOKです
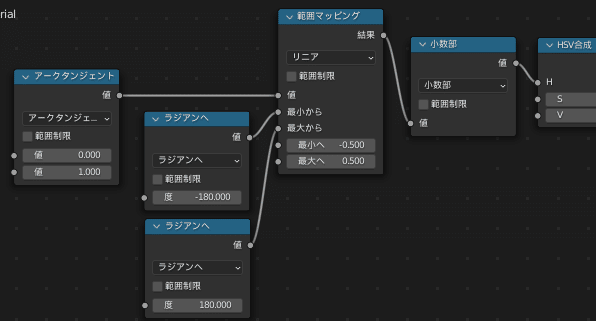
簡単に説明すると、
数式ノードの「ラジアンへ」で $${-π}$$ と $${π}$$ を取り出す
「範囲マッピング」ノードで $${-π}$$ から $${π}$$ の範囲を、 $${-0.5}$$ から $${0.5}$$ の範囲にマッピングする
数式ノードの「小数部」で、負の値が $${0.5}$$ から $${1.0}$$ の範囲に来るようにする(例えば-0.2は小数部を通すと0.8になります)
という処理が行われます
属性を設定する
あとは球面調和関数の値を持ってくればいいわけですが、これには「属性(Attribute)」というものを使っていきます
Blenderではジオメトリの頂点や辺、面などに数値やベクトルなどを紐付けたい場合に属性が使われます
今回は各頂点に球面調和関数の値(複素数)を紐付けたいので、floatではなくベクトルを使うことにしてxに実部、yに虚部を割り当て、zは無視することにし、ベクトルの属性を作成します
属性は名前で指定します
属性ノードを作成し、SphHarmYという名前でアークタンジェント2に接続します(SphHarmYはこだわりなどあれば別の名前でも構いません)
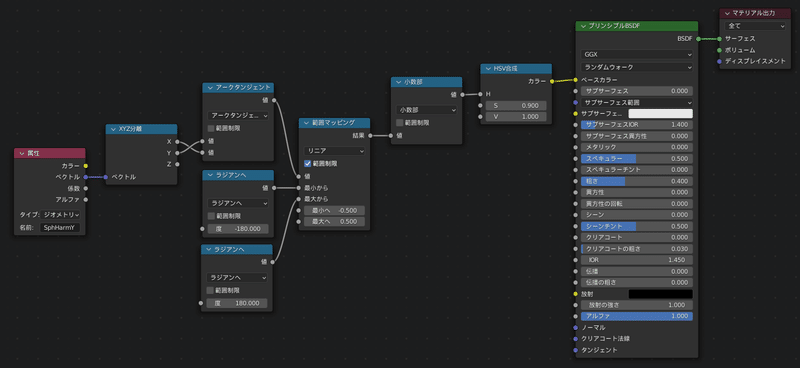
XYZ分離ノードを使ってアークタンジェント2に繋ぐ
XとYの繋ぐソケットに注意
これでマテリアル側で属性を受け取る準備が整いました!
ではGeometry Nodesのタブに戻ります
Geometry Nodesのタブでは3Dビューポートの表示がデフォルトで「ソリッド」になっているので「マテリアルプレビュー」に変更します
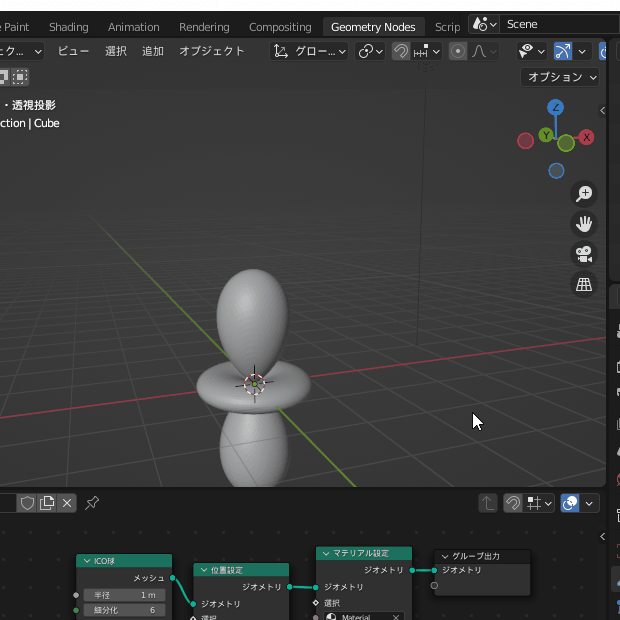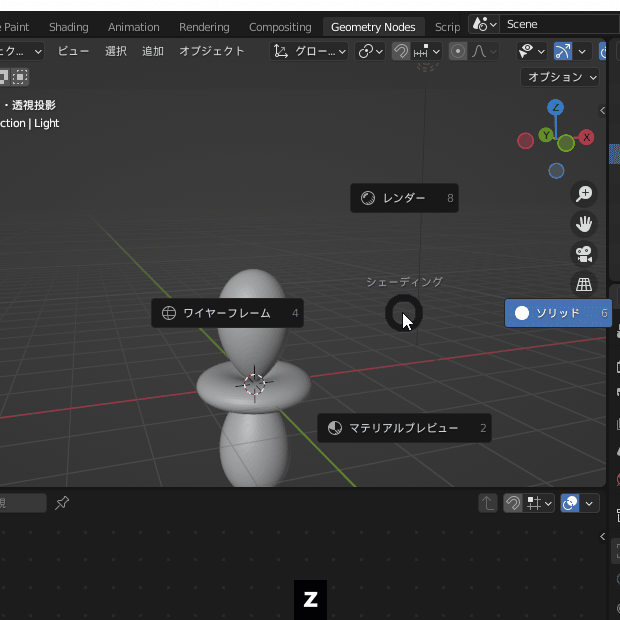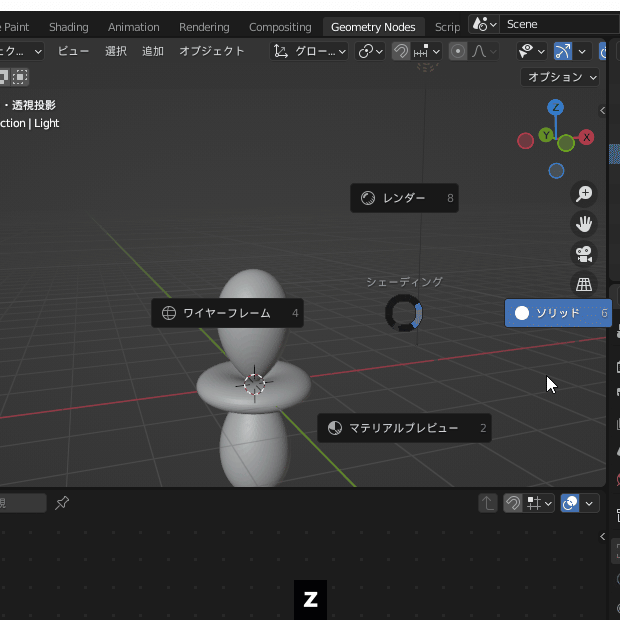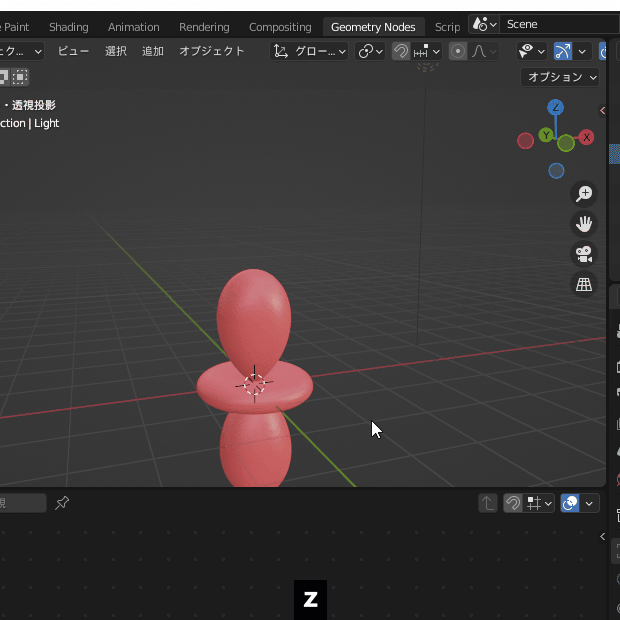
マテリアルプレビューを選択します
ではジオメトリに属性を作成していきます
属性を作成するにはまずグループ出力に新しいベクトルの出力を追加します
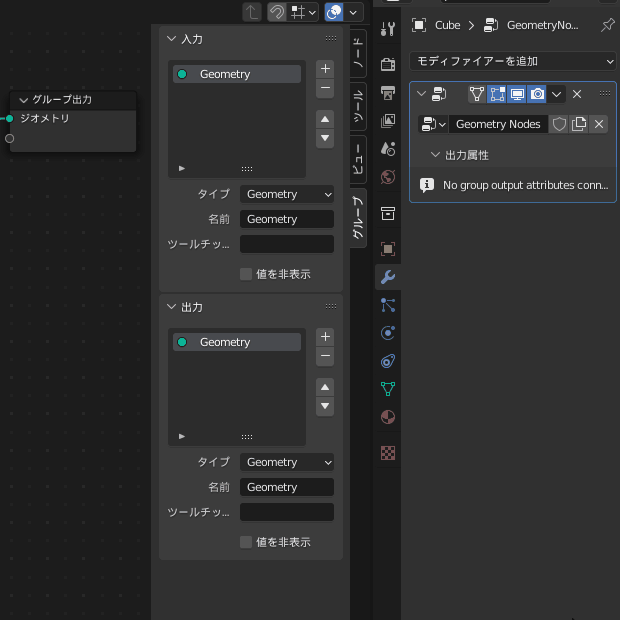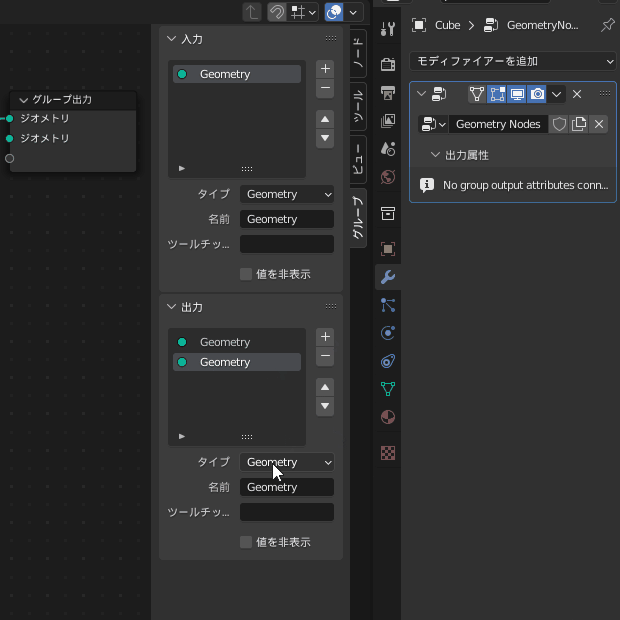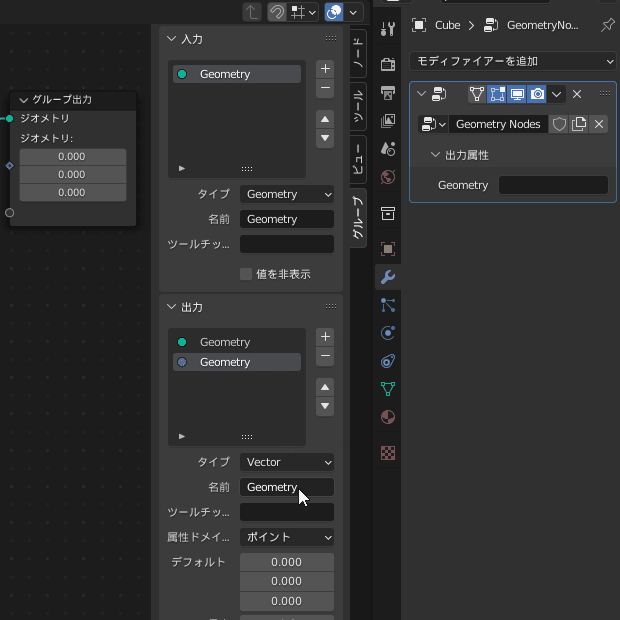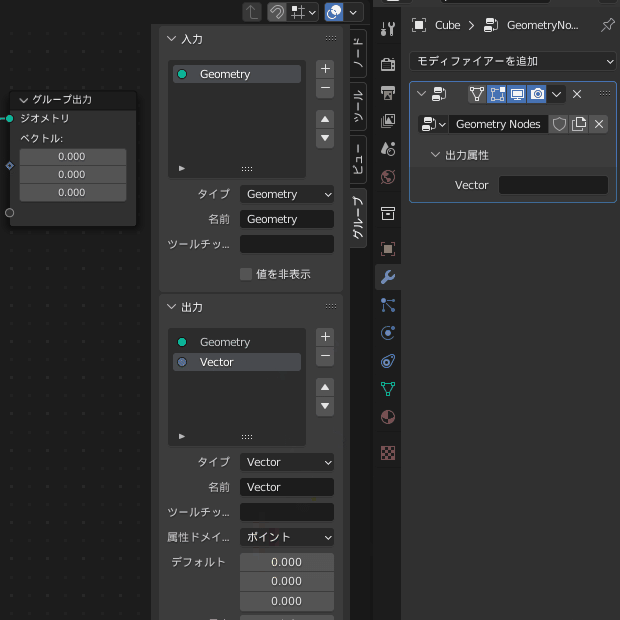
ジオメトリノードエディタ上にカーソルがある状態で N キーで右からパネルが出現します
よく見ると右側の「出力属性」というところにも「Vector」が追加されています
ここに属性名「SphHarmY」と書くとその名前の属性が追加されます
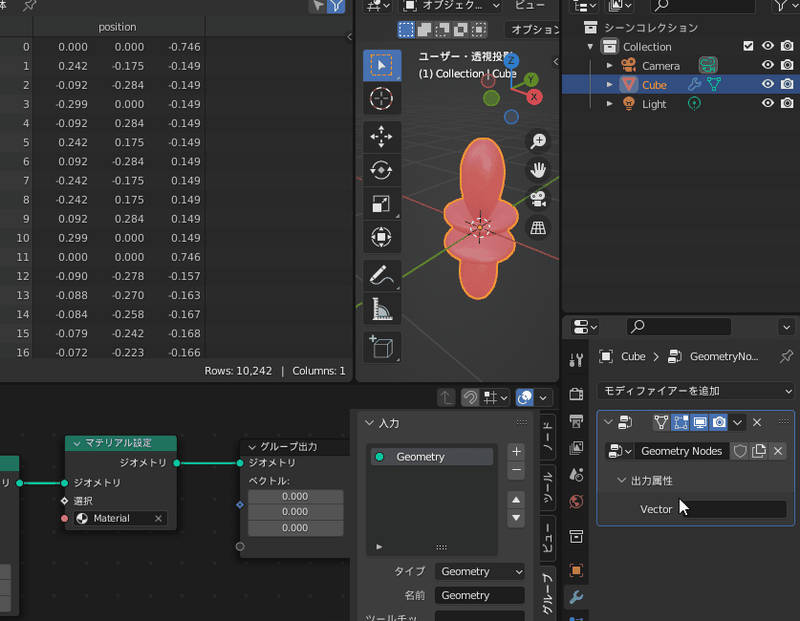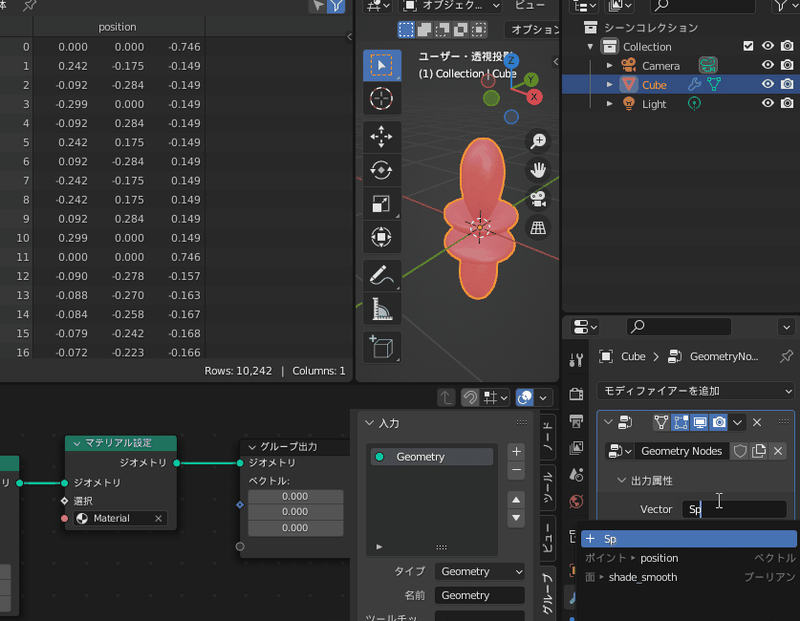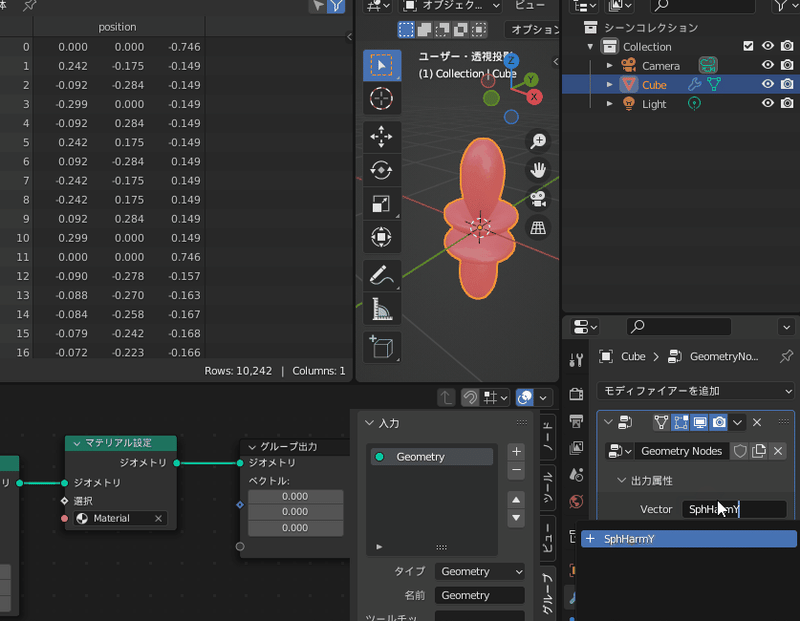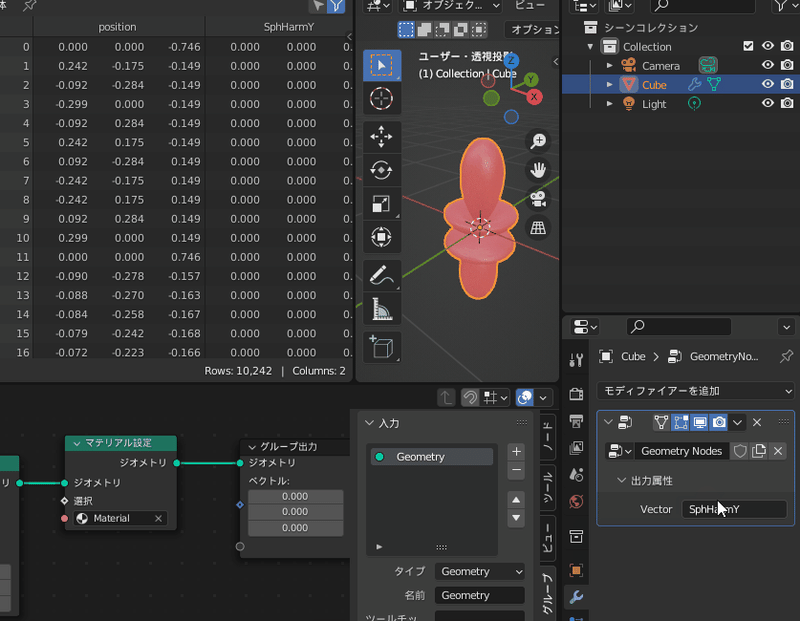
左上画面に注目すると、各頂点にSphHarmYという名前の属性が追加されたのがわかる
試しにグループ出力の値を変更してみると、確かにこれらの値をもとに色が変わるのが確認できます
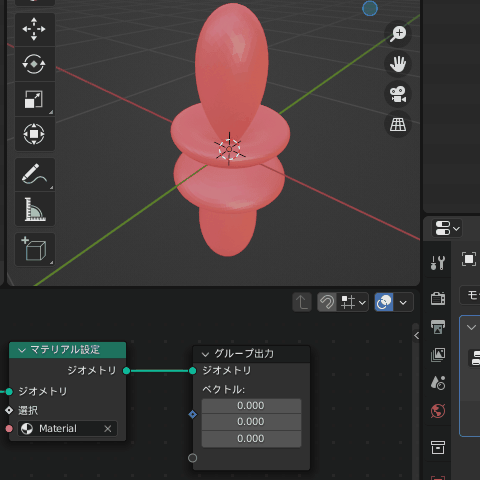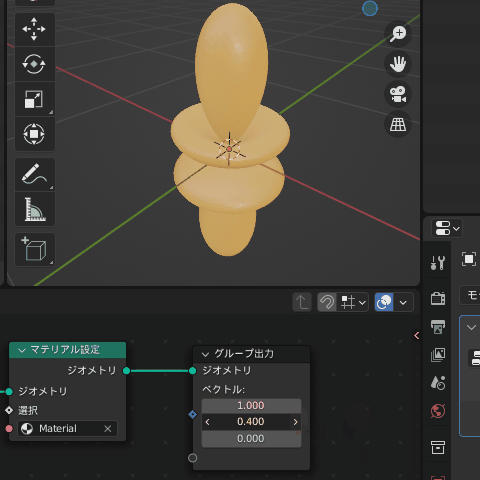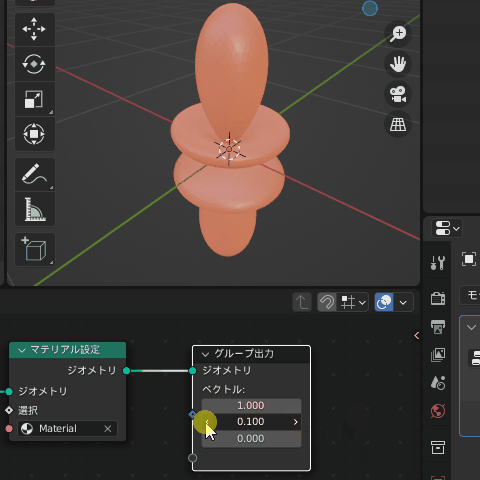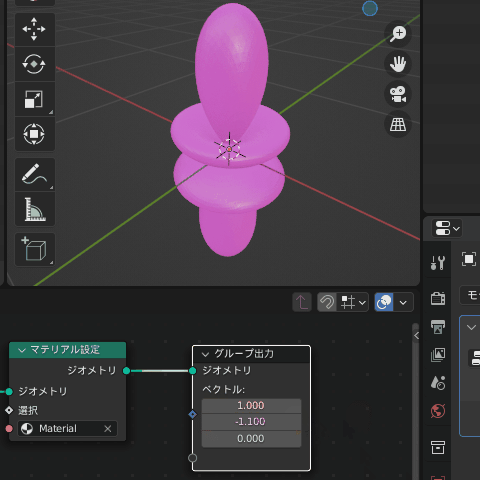
属性が作成できたので、さっそく計算した球面調和関数の値を流してみましょう!
とはいえ、ここまで実数しか扱ってきませんでしたので今のところは単純に正負のみの判定となります
(この記事では値が正なら赤、負ならシアンになります)
「ベクトル合成」ノードを使って球面調和関数の絶対値を挟む直前の値をグループ出力のx座標に繋げばうまくいきま……あれ……?

なにか様子が変です
$${Y_2^0(θ, ϕ)}$$ の正負はこんな変な場所で変わるはずはなく、正しくは次の画像のように浮き輪のような箇所だけ色が変わるはずです
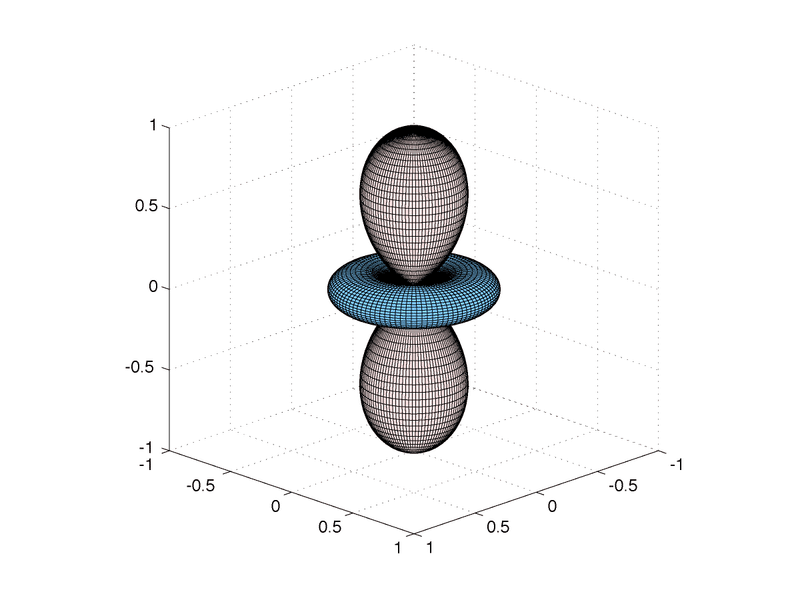
実はこれが Geometry Nodes 最大の落とし穴(だと私は思っています)で、同じノードから伸びていても次のノードに渡される値が同じとは限らないのです
なぜこのようなことが起きてしまうのかというと理由は簡単で、下図の2の「Real」が球面調和関数の値を拾おうとするときには1の位置設定ノードが位置を変えた"後"の位置座標を使って再計算を行ってしまっているためです
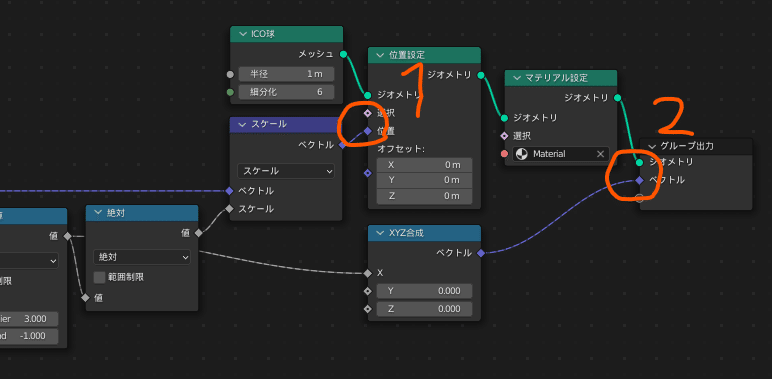
グループ出力ノードが計算する際には、位置設定後の値が使われてしまう
つまり、一部のノード(これをフィールドという)では都度計算が行われるわけです
先程ソケットの形状の話をしましたが、
・丸い形状のものはフィールドにはならないソケット
・ひし形の形状のものはフィールドを構成する事ができるソケット
を意味します
ソケット同士を繋いでいる線の形状も、
よく見ると「実線」と「破線」がありますが、
・実線はフィールドではない繋がり
・破線はフィールドになっている繋がり
を意味します
このあたりはやや込み入っているのでフィールドについての詳しい説明は先程も貼った別記事にまとめました
一応知らなくても先には進めるように書きましたが、理解を深めたい方はご覧ください
ノードごとに都度再計算されてしまうと、困ってしまいますが、
もちろんこれは回避する方法が用意されています
それには「属性キャプチャ」ノードを使います
位置設定ノードの直前に属性キャプチャノードを挟んでおき、
位置ノードのベクトルを予めここに流しておくことで、
その時点での位置ベクトルを保持しておくことができます
そして今まで位置ノードから直接ベクトルを受け取っていたノードに対してすべて属性キャプチャを通すようにすれば、
常に位置設定が行われる前の位置ベクトルが使われることが保証できるわけです

全てを属性キャプチャノード経由で位置を利用するよう繋ぎ直すと、想定通りの結果になった
球面調和関数をつくる
さて、ようやくですが本題の球面調和関数のパートです!(汗)
もちろんさっきまでやっていたように球面調和関数表とか見てを書いても良いのですが、理想的には $${l}$$ と $${m}$$ を指定したらちゃんとそれに相当する $${Y_l^m(θ, ϕ)}$$ の3Dモデルに切り替わるようにしたいものです
まずは球面調和関数の式を確認したいところですが、
文献によって若干バリエーションがあるので注意が必要です
この記事ではこれ以降、
Wolfram Alphaに定義のあるものは全てそれに準じることにします
従ってこちらを参照し、
$$
Y_l^m(θ, φ) = \sqrt{\frac{(2l+1)}{4π}\frac{(l-m)!}{(l+m)!}} \, P_l^{m} ( \cos θ ) \, e^{i m φ}
$$
この式を組み立てていくことにします
しかし四則演算や平方根や指数関数などは数式ノードを使えば良い一方で、以下の2つは一筋縄ではいかなそうです
階乗 $${!}$$
ルジャンドル陪多項式 $${P_l^m(\cos{θ})}$$
このうち、階乗はすぐに解決できます
階乗の近似を行う
階乗には有名な近似(スターリングの近似)があり、精度によっていくつかバリエーションがありますが、例えば次のような式です
$$
n! ≒ \sqrt{2 π n}(\frac{n}{e})^n(1+\frac{1}{12n})
$$
この式であればBlenderでも扱えそうです!
しかし、たくさんの演算が使われていてノードで扱うのはちょっと大変そうですし、
なによりこの式は $${n=0}$$ のときはゼロ除算が含まれてしまったり、
全体に$${\sqrt{n}}$$ がかかっていたりするので、
n=0だけ場合分けしないといけないのが少し面倒です
ここで一つ重要な情報ですが、Blenderでは $${0^0 = 1}$$ と定義されています
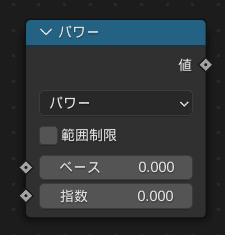
それを踏まえてちょっとした変形とさらなる近似を加えてやると
$${n=0}$$のときの条件分岐を書かずに済み、
結論から言うと、今回の場合次のような近似式を使うと便利です
$$
n!≒(\frac{n}{e})^n \sqrt{2 π n+\frac{π}{3})}
$$
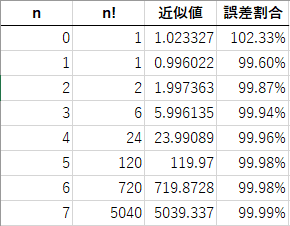
可視化には十分な精度だと思います
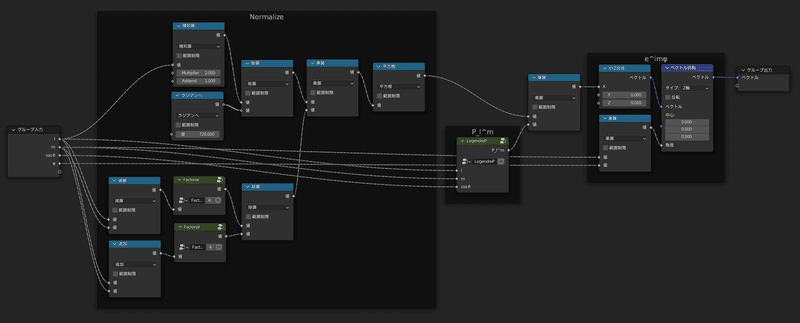
実際に先程の数式をノードとして並べるとこのようになります
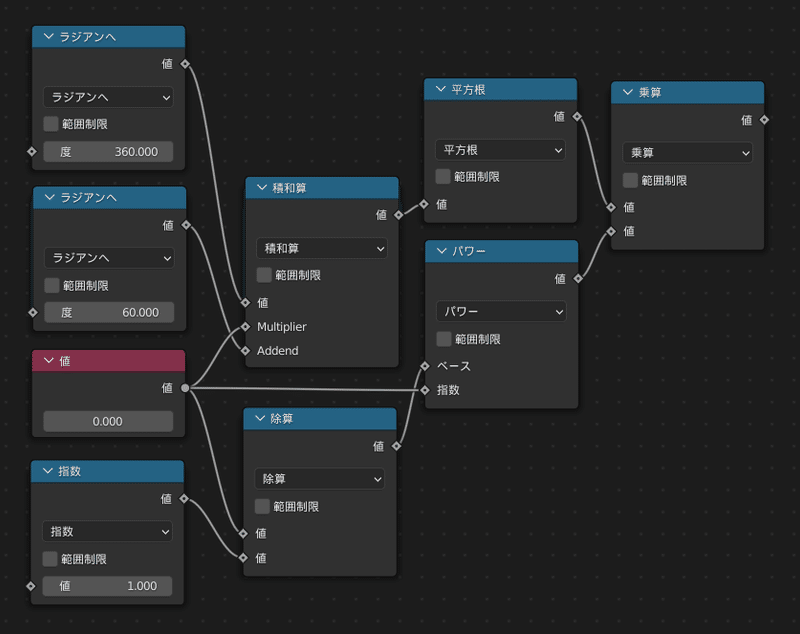
これらのノード群をこのまま使っても支障はないですが、
複数箇所で再利用したい場合、ノードを「グループ化」すると便利です
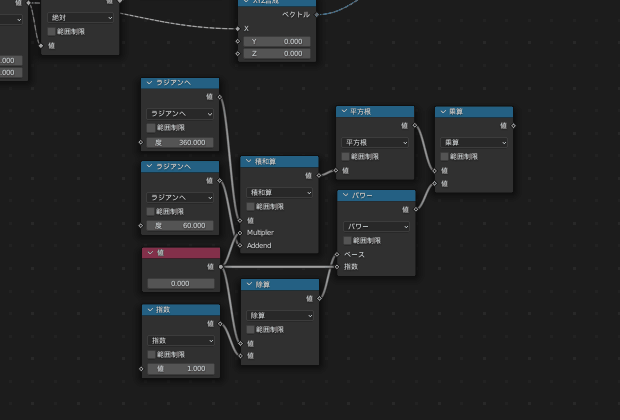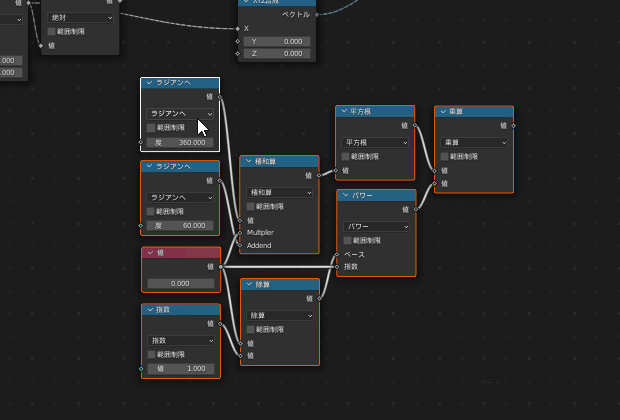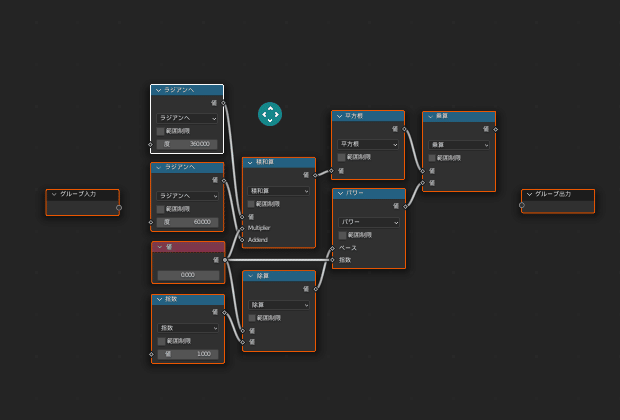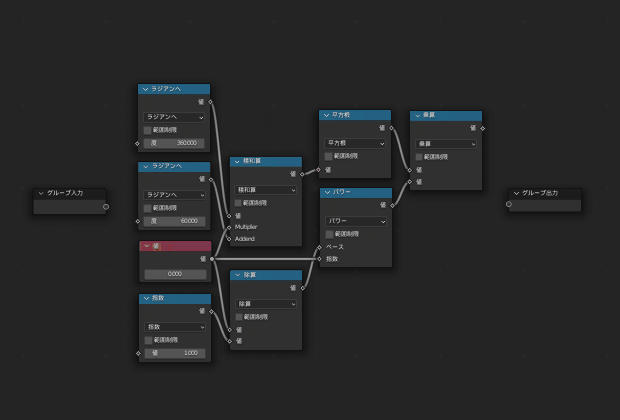
グループは
「グループ入力」から入力を受け取り、
「グループ出力」から値を出力する、
というのが基本構成です
これに従い、次の画像のように繋いで「階乗」のグループとします
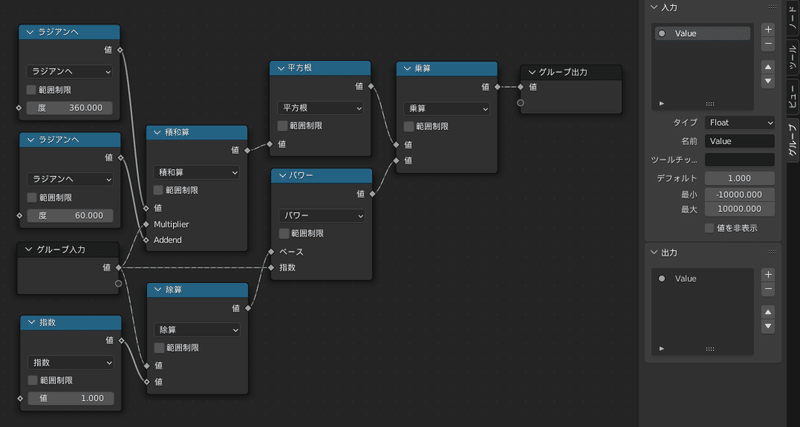
入力名と出力名を変更したい場合、Nキーを押して「グループ」タブから変更できます
もとのGeometry Nodesに戻るには、
右上の上矢印ボタンを押してひとつ上の階層に戻ります
逆に、グループを編集するにはグループのノードの右上のアイコンをクリックします
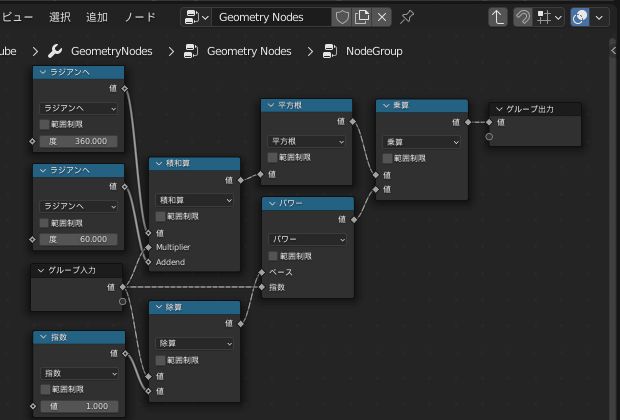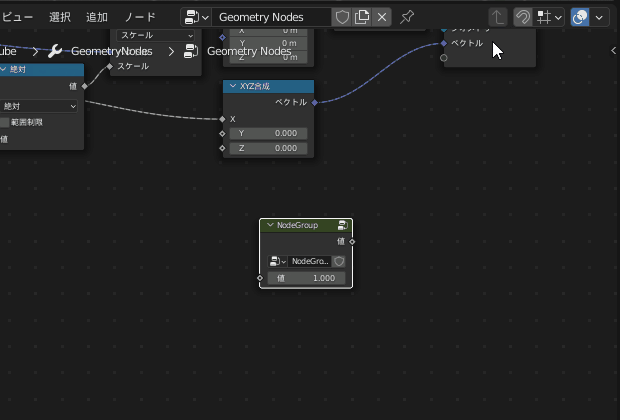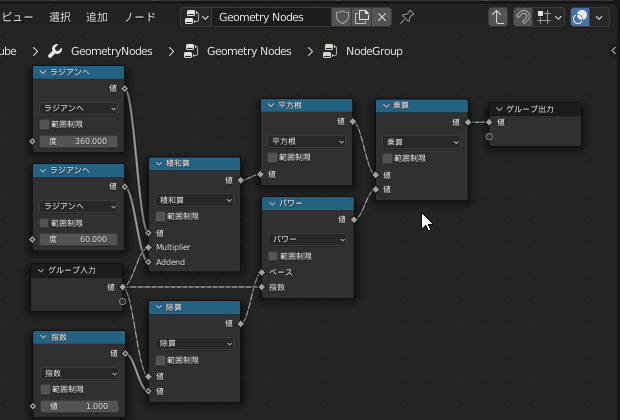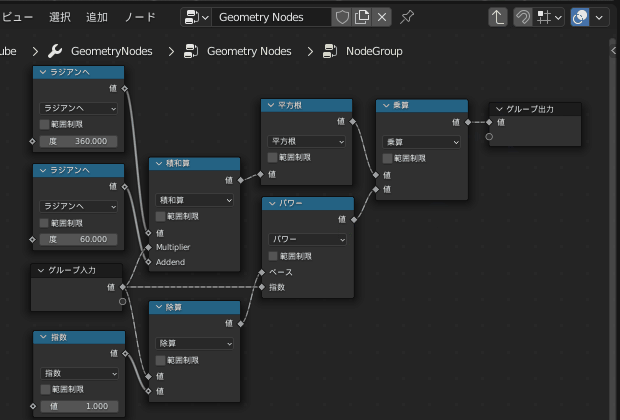
グループ化したことにより、
あたかも「階乗」ノードがあるかのように扱うことができるようになりました!
仕上げに、わかりやすい名前をつけてあげましょう
ルジャンドル陪多項式の確認
ここからがこの記事最後の山場です!
ルジャンドル陪多項式は $${P_l^m(\cos{θ})}$$ で表される多項式で、
先程の球面調和関数の式、
$$
Y_l^m(θ, φ) = \sqrt{\frac{(2l+1)}{4π}\frac{(l-m)!}{(l+m)!}} \, P_l^{m} ( \cos θ ) \, e^{i m φ}
$$
に登場します
ルジャンドル陪多項式には次のような式が成り立ち、
これを利用すると便利です
(これらの式は英語版Wikipediaを参考に式変形を行いました)
$$
\begin{align*}
&(1) P_{|m|}^m(\cos{θ}) = \frac{(|m|+m)!}{|m|!} (\frac{\sin{θ}}{-2 \mathrm{sgn} m})^{|m|} \\
&(2) P_l^m(\cos{θ}) = \frac{(2l-1)\cos{θ}P_{l-1}^m(\cos{θ})+(1-l-m)P_{l-2}^m(\cos{θ})}{l-m}
\end{align*}
$$
(なお、$${P_{|m|-1}^m(\cos{θ}) = 0}$$ とみなして良い)
(また、$${\mathrm{sgn}}$$は符号関数)
これらの式を使えば $${0≦|m|≦l}$$ であるような全ての $${P_l^m(\cos{θ})}$$ の値が求まることがわかります
ルジャンドル陪多項式の漸化式の初期値を求める
まずは先程の $${(1)}$$ 式を組み立てます
この式もグループ化しましょう
適当に新規作成した数式ノードなどを選択して Ctrl + G で手早く新しいグループが作成できます
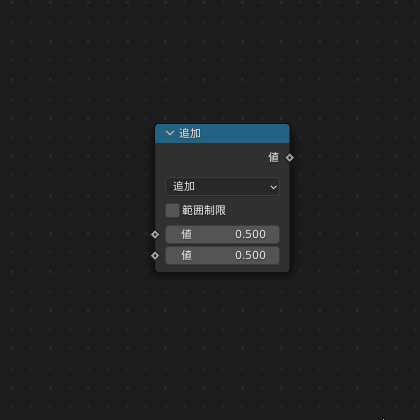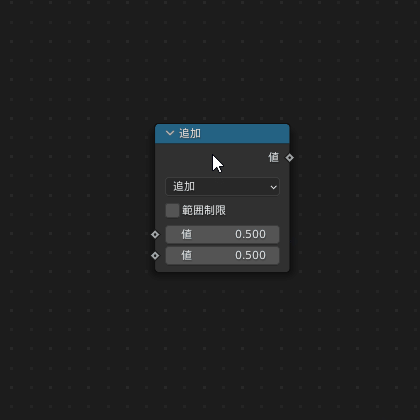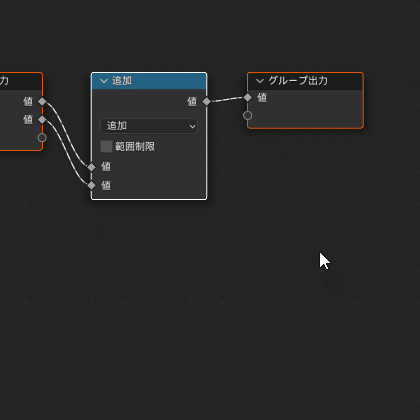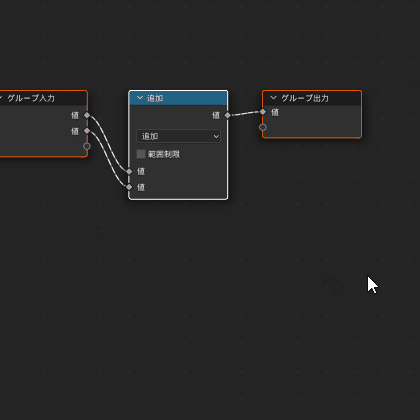
あとは $${(1)}$$ のとおりにノードを作って繋げるだけです
先程作成した階乗ノードはグループから見つかります
次の画像が $${(1)}$$ 式を計算するグループの完成図です
グループの名前は「P_|m|^m」としておきます
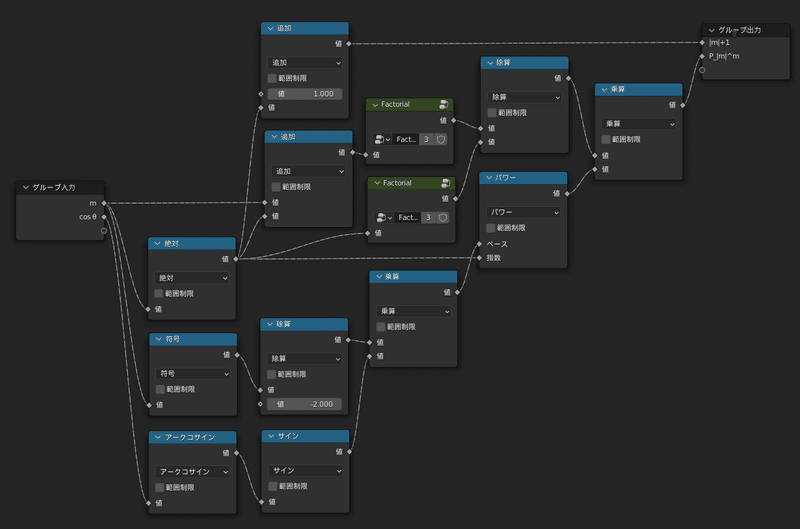
上の完成図では出力にこっそり $${P_{|m|}^m(\cos{θ})}$$ だけではなく $${|m|+1}$$も一緒に追加していますが、
これはすぐ後で使いますので、騙されたと思ってとりあえず加しておいてください
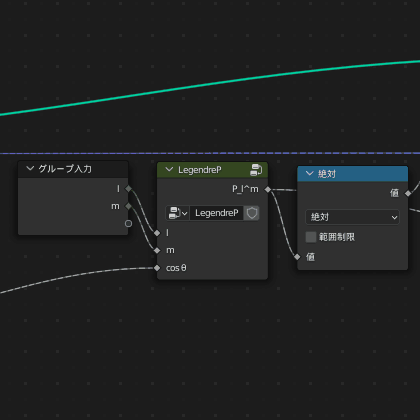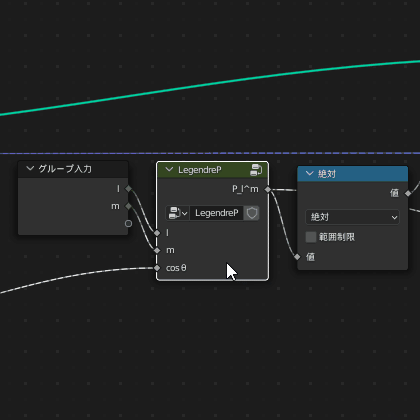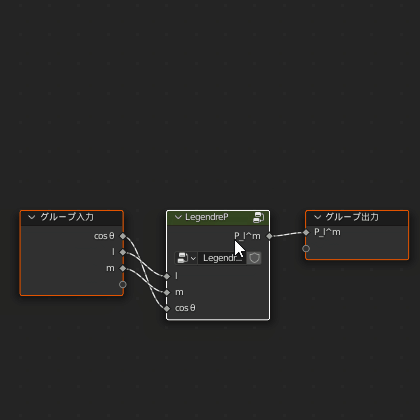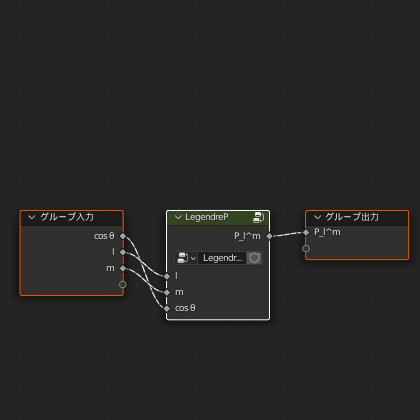
ルジャンドル陪多項式の漸化式を計算する
さて、次に作るべき $${(2)}$$ 式は漸化式です
Blenderで漸化式を扱うにはどうすればよいでしょうか?
私も試行錯誤したのですが、結論としては次のようにするのが良さそうです
詳しい説明はあとでしますので、一旦画像を見てください
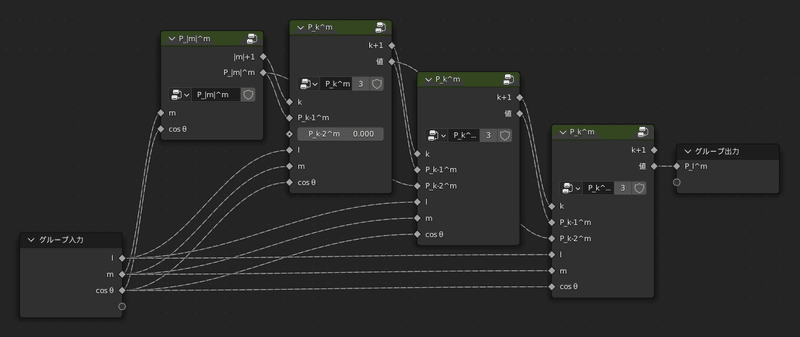
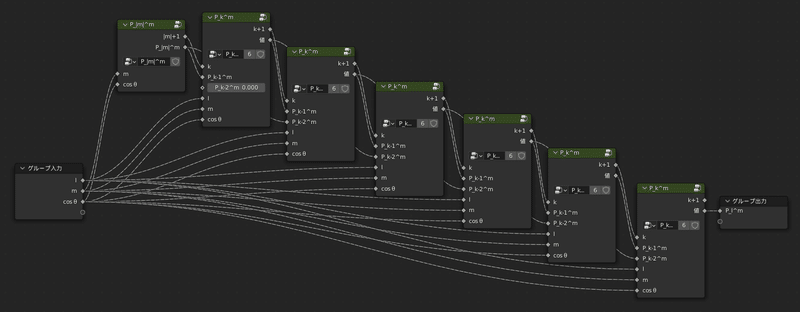
名前は「LegendreP」とした
上の画像中「P_|m|^m」は先程作ったグループで、
その他3つ並んでいる「P_k^m」というグループの中身は
漸化式を解くために作った新しいグループで、中身は次の画像の通りです
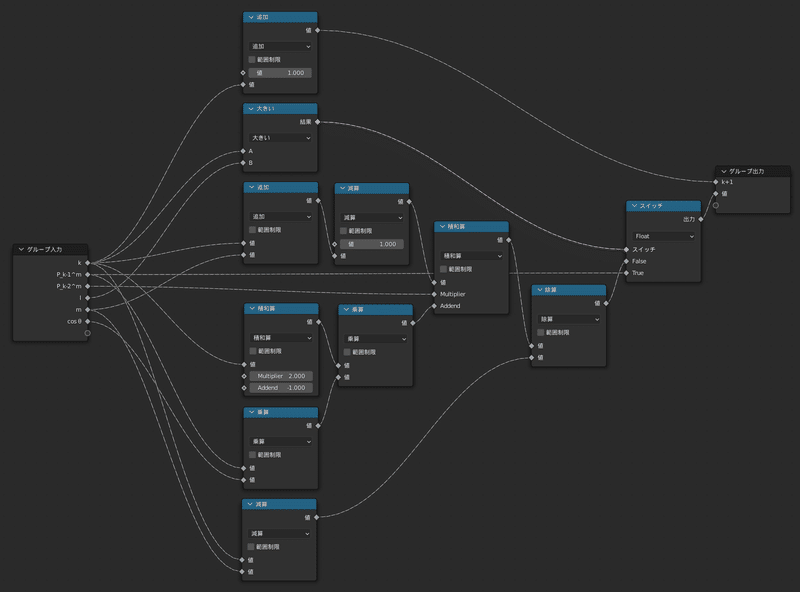
名前は「P_k^m」とした
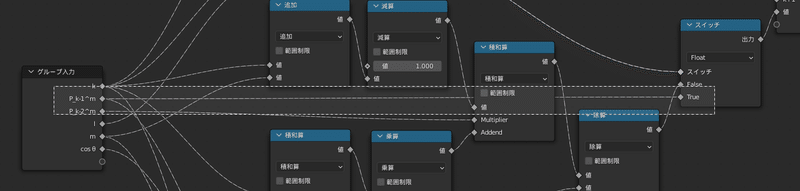
このグループの一番のポイントは、
最後に「$${k}$$」と「$${l}$$」を大小を比較して条件分岐を行っているところです
もし$${k≦l}$$であれば計算が必要とみなし、計算した値を出力します
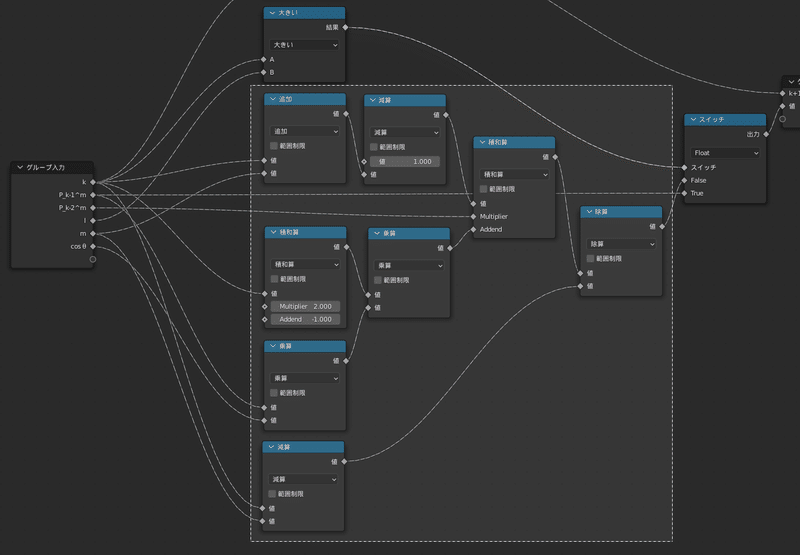
一方で$${k≦l}$$でないならばこれ以上の計算は不要と判断し、
一つ手前の値をそのまま出力します
これにより、この「P_k^m」ノードを適切に次々繋いでいけば、
一番最後のノードからは求めたかった値が出力される、という算段です!
ただし残念にも当然ながら、求まる$${P_l^m(\cos θ)}$$の値は
$$
l ≦ (並べたP_k^m漸化式ノードの数)
$$
までということになります
少なくとも $${l≦3}$$ まで計算できれば電子軌道でいうところのf軌道までカバーできますし、これで妥協しよう……というわけです
もちろん並べるノードの数を増やせばもっと大きな $${l}$$ の値にも対応できますので、もっと頑張れる人はたくさん繋いでみても良いでしょう
さて、これでルジャンドル陪多項式のグループは完成です!
ここまでうまくいっているかどうか、
実際に新しく作ったノードに置き換えて確認してみましょう
確認用にするために一番上階層のGeometry Nodes(下の画像のもの)のグループ入力に整数タイプの入力「l」と「m」を追加し、
こちらも繋いでおきます
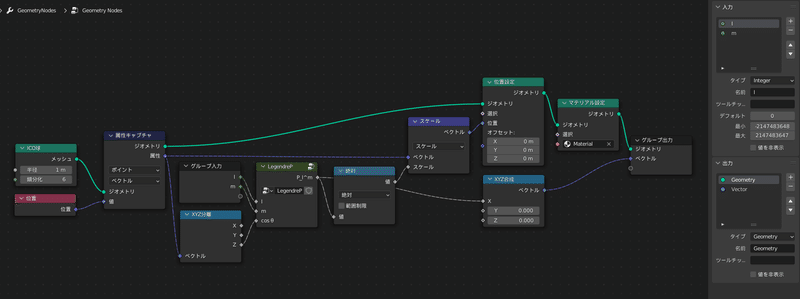
そして $${l}$$ の値を変えると……

さっき漸化式のノードを頑張って6個繋いだのでl=6まで対応している
このようになっていればここまでは成功です!
(漸化式のノードを繋いだ分だけ $${l}$$ の値が反映されるので、3つしか繋いでない場合は $${l=4}$$ 以降形が変わりません)
(うまくいっていない場合は線の繋ぎ位置や、ノードに直接入力すべき数値、数式ノードの種別などを確認してみてください)
なお、$${m}$$の値を変動させた場合は、現状このようになります

球面調和関数グループを作成し入出力を整える
ここまでくればあともう少しです!
一旦もう一度球面調和関数の形をおさらいしておきます
$$
Y_l^m(θ, φ) = \sqrt{\frac{(2l+1)}{4π}\frac{(l-m)!}{(l+m)!}} \, P_l^{m} ( \cos θ ) \, e^{i m φ}
$$
あと残すは、
$$
\sqrt{\frac{(2l+1)}{4π}\frac{(l-|m|)!}{(l+|m|)!}} e^{i m φ}
$$
の部分だけです!
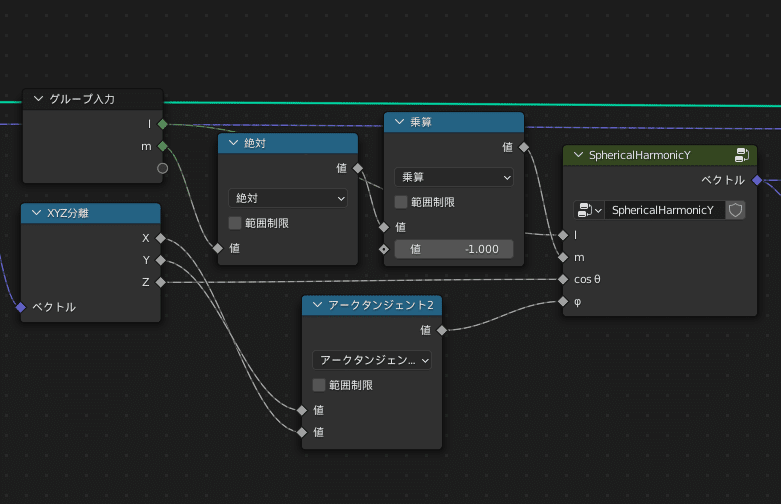
まず先に $${(x,y,z)}$$ 座標から $${φ}$$ を取り出しましょう
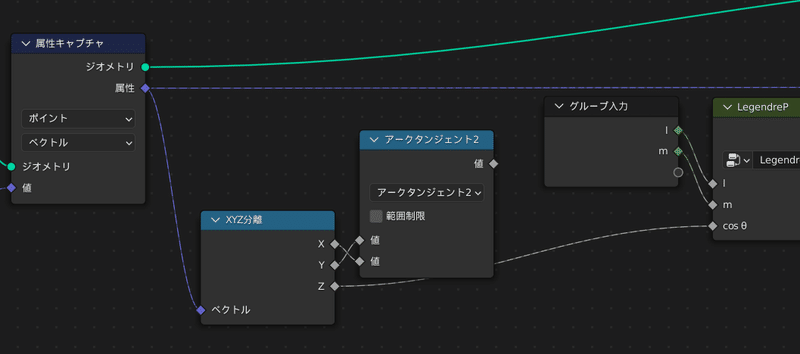
これで球面調和関数の材料となる $${l,m,\cos θ, φ}$$ が全て準備できたので、
いよいよ球面調和関数のグループを作成します
名前は「SphericalHarmonicY」とします
接続や名前を引き継いでくれるのでちょっと楽です
先に「SphericalHarmonicY」グループの入出力の設定をします
入力「φ」を追加
出力の名前は「Vector」とし、型もベクトルに変更
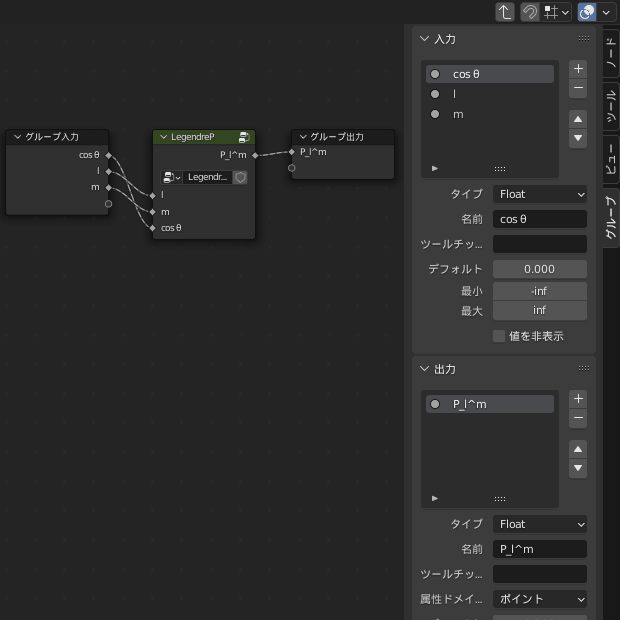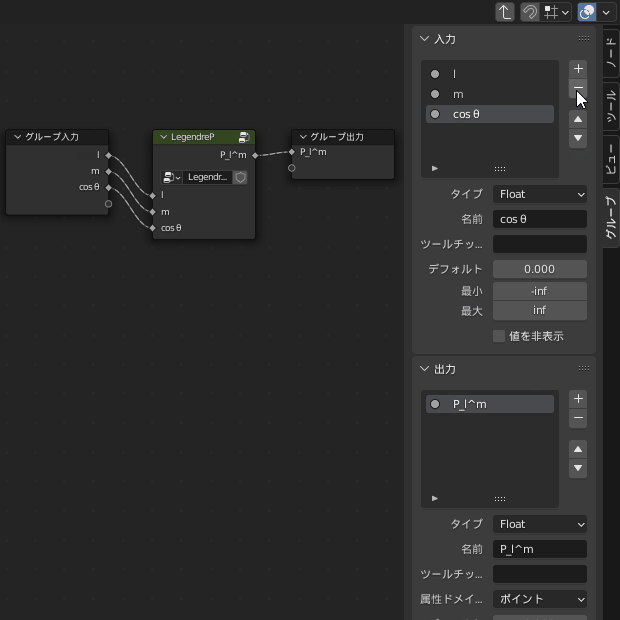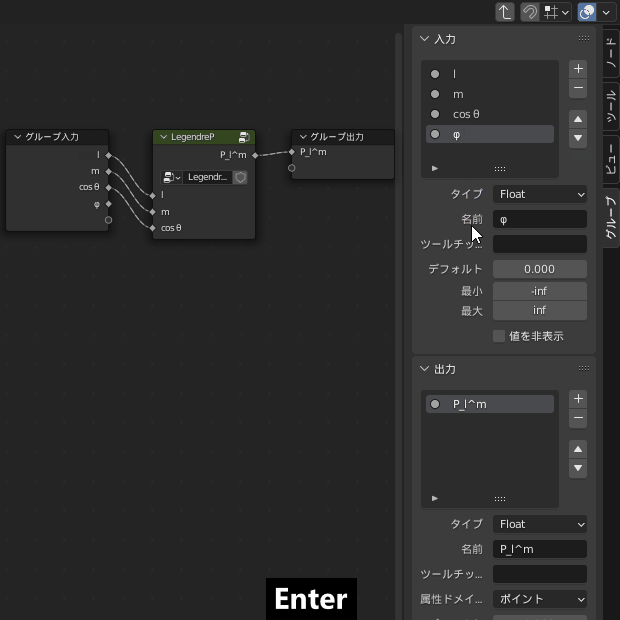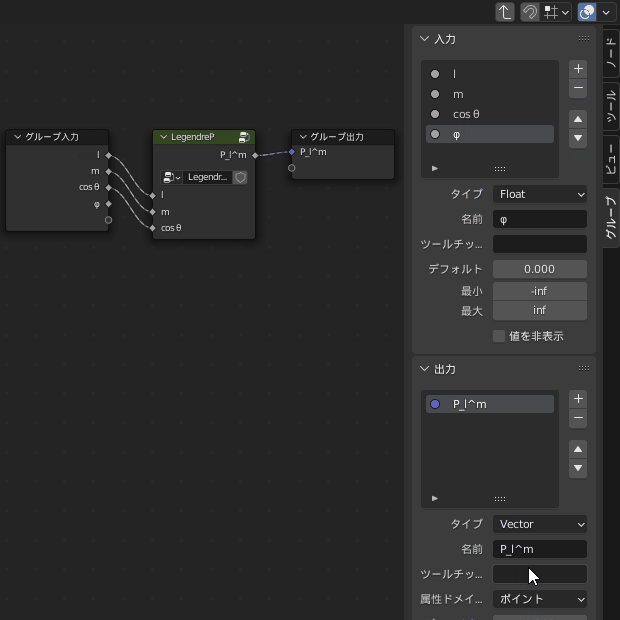
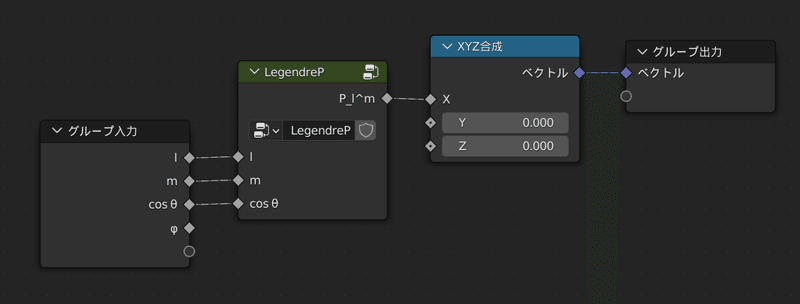
また、LegendrePノードの出力はXYZ合成ノード経由でベクトル変換しておきます
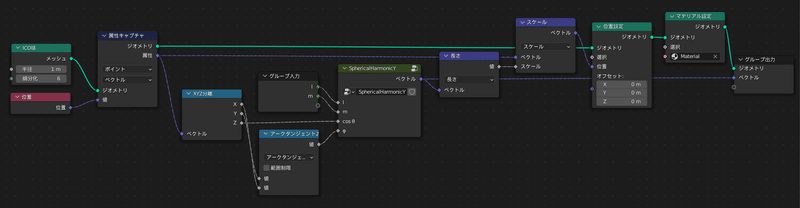
ここまでできたらもう一度元のGeometry Nodesの階層に戻り、
入力「φ」が増えたり、出力がfloatからベクトルに変わったりしたのでその対応をします
アークタンジェント2ノードからφへ繋ぐ
絶対ノードはベクトル演算「長さ」ノードに置き換えて繋ぎ直す
XYZ合成ノードは消してSphericalHarmonicYノードの出力をそのままグループ出力に繋ぐ
球面調和関数を計算する
さて、諸々細かな準備が整ったので、
あとはSphericalHarmonicYグループ内で球面調和関数を組み立てていきます
まずは$${e^{imφ}}$$部分をつくってLegendrePノードと合わせます
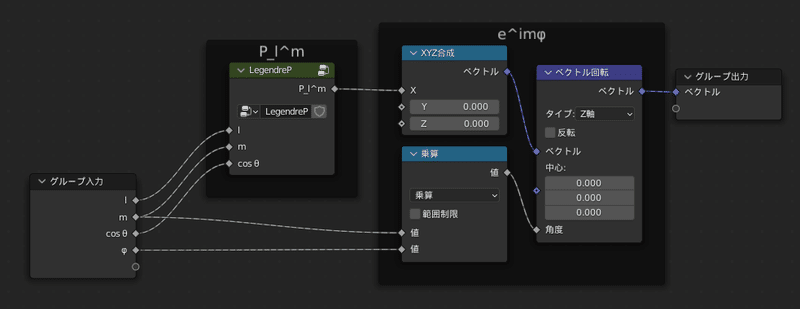
なくても計算結果には影響しないが、見たときにわかりやすい)
いきなり結構テクいことをしていますが、やってることはシンプルで、
$${(Y_l^{m},0,0)}$$ をZ軸を中心に $${mφ}$$ ラジアンだけ回して虚数の積実現しています
(この記事では3次元ベクトルを、$${x}$$が実部で$${y}$$が虚部とする複素数として扱うことを思い出してください)
(もちろん、オイラーの公式を使って計算しても問題ないです)
最後に、残りの正規化部分を追加すれば球面調和関数の完成です!
さて、$${l, m}$$の値を変えて形を確認してみましょう!

おや、なんだか虹色できれいですが、
どうも目標としていた形状とはどうも違いそうです
実関数表示を行う
実はちゃんと、「球面調和関数」としては間違いなくこれで完成です
しかし、当初目標としていた形状は以下のようなものでした
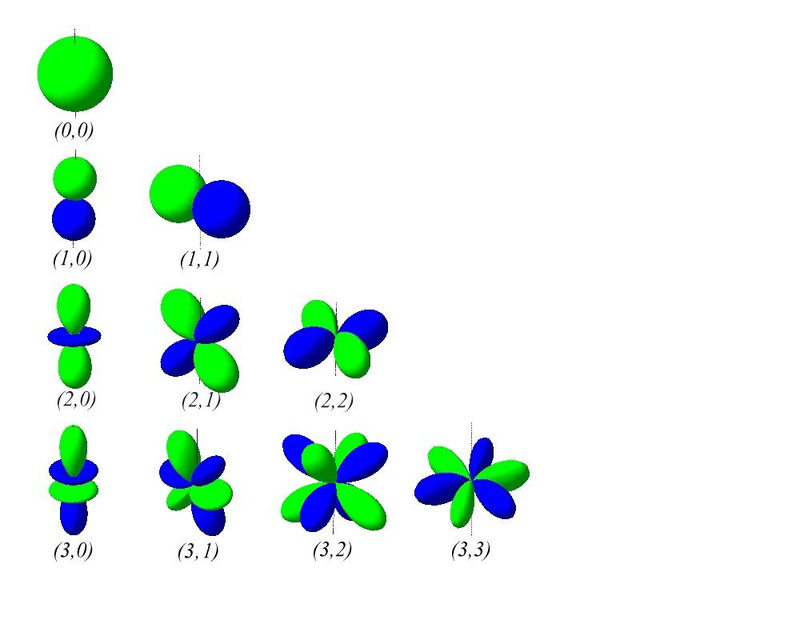
Wikimedia Commons より 作成 : Hellingspaul
この"当初目標としていた形状"は球面調和関数の「実関数表示」と呼ばれるものです
この記事でこれまで扱ってきた、複素関数であるところの球面調和関数$${Y_l^m}$$と区別するため、
$$
Y_{l m}
$$
のように、$${l}$$と$${m}$$が両方下付きの記号を用いて実関数表示の球面調和関数を表すことにします
実関数表示には選び方に自由度があるのですが、
この記事では球面調和関数の英語版Wikipediaにある次の式に習って実関数表示を行うことにします
$$
\begin{align*}
Y_{l m} &= \begin{cases}
\dfrac{i}{\sqrt{2}} \left(Y_l^{m} - (-1)^m\, Y_l^{-m}\right) & \text{if}\ m < 0\\
Y_l^0 & \text{if}\ m=0\\
\dfrac{1}{\sqrt{2}} \left(Y_l^{-m} + (-1)^m\, Y_l^{m}\right) & \text{if}\ m > 0.
\end{cases}\\
\end{align*}
$$
ところで、球面調和関数の複素共役について次のような関係が成り立ちます
(ここでは複素共役をアスタリスク $${*}$$ で表すことにします)
$$
Y_l^{m}{}^* = (-1)^m Y_l^{-m}
$$
これを踏まえて次のように式変形を行うと組み立てやすいです
$$
\begin{align*}
Y_{l m} &= \begin{cases}
\dfrac{i}{\sqrt{2}} \left(Y_l^{-|m|} - Y_l^{-|m|}{}^*\right) & \text{if}\ m < 0\\
Y_l^0 & \text{if}\ m=0\\
\dfrac{1}{\sqrt{2}} \left(Y_l^{-|m|} + Y_l^{-|m|}{}^*\right) & \text{if}\ m > 0.
\end{cases}\\
\end{align*}
$$
こうすることでSphericalHarmonicYノードに流す$${m}$$を$${-|m|}$$に変更すれば3つのケース全てで使うことができます
続いて、球面調和関数の複素共役をとります
この記事では複素数を3次元ベクトルで代用しているので、
複素共役をとる操作はY座標を反転させる操作に相当します
ベクトル演算「乗算」ノードを利用し $${(1,-1,1)}$$ を乗算することで、
Yのみ要素を反転します
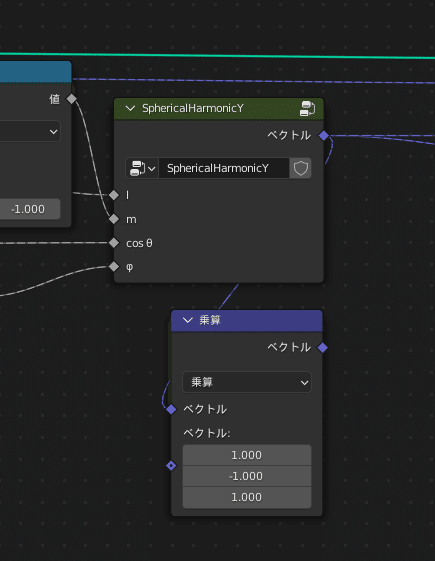
もとの値と共役な値とを対称的に見せる意図があります
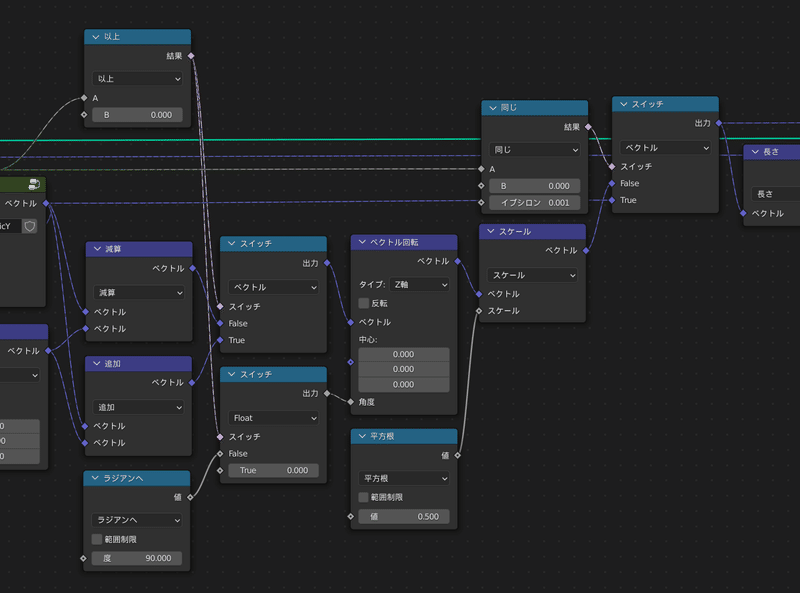
あとは、
$${m≧0}$$なら和をとってZ軸に0度回転して$${\sqrt{\frac{1}{2}}}$$倍
$${m<0}$$なら差をとってZ軸に90度回転して$${\sqrt{\frac{1}{2}}}$$倍
という分岐を行ってから、
$${m=0}$$ならSphericalHarmonicYの出力を直接使う
$${m≠0}$$なら上の条件分岐後の値を使う
というように制御してやれば、実関数表示も完成です!
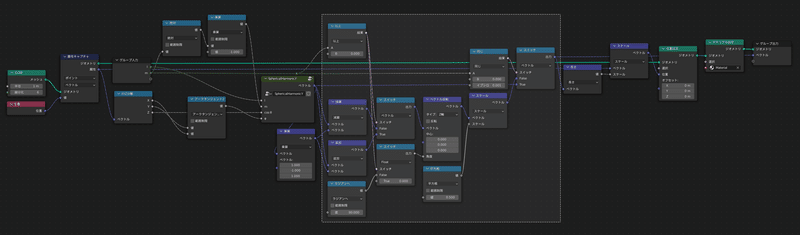
矩形選択しているところが最後に新しく追加したノード
それでは、今度こそ目標としていた形状になっているはずです!
$${l, m}$$の値を変えて形を確認してみましょう!

これで完成です!お疲れさまでした
参考文献
Wolfram Alpha
spherical harmonics
associated Legendre polynomials
n!
球面調和関数の定義、複素共役の関係式、ルジャンドル陪多項式の定義はこの記述に従っています
階乗はn=∞における級数展開をもとに式変形を行い、
今回使った階乗の近似式を導きました
Wikipedia
Spherical harmonics
Associated Legendre polynomials
定義がWolfram Alphaと同一であることを確認した上で、
球面調和関数の実関数表示、ルジャンドル陪多項式の漸化式やその他関係式はこの記述に従っています
ブログ等
tsujimotterのノートブック「日曜化学:量子力学の基本と球面調和関数の可視化(Python/matplotlib)」
tsujimotterさんによる2021年7月の空前の球面調和関数ブームを巻き起こした記事です
これを読んでもう一度ブームを再燃させようと思い記事執筆に至りました
EMANの量子力学「原子の構造」
言わずとしれたEMANの物理学シリーズ、EMANの量子力学より球面調和関数の導出のあるページです
こちらで理解を深めました
その他
OEIS
式変形等の考察に役立ちました
さいごに
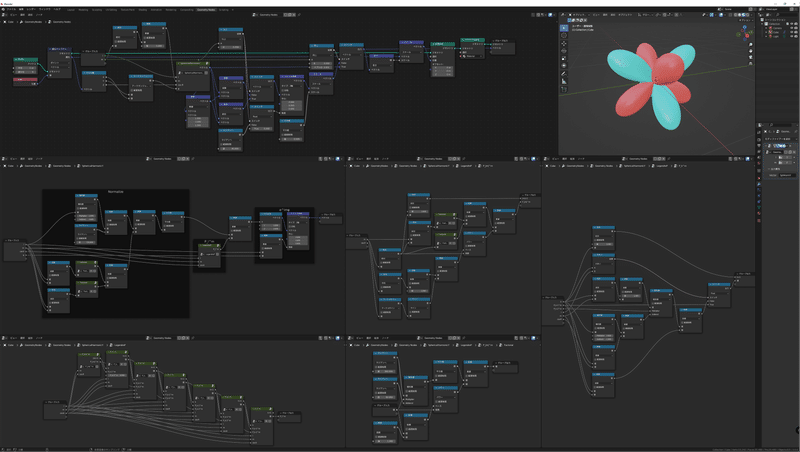
ノード全図
動作確認済みのノード全図です(4K画像)
作っていてもしちゃんと動かなかったら、
こちらを参考に修正していただければと思います
その他不明な点、質問、誤り等ありましたら、Twitter(@MelvilleTw)にて連絡いただければと思います
もしよければ…
もしこの記事の反響が良ければ、
水素原子の電子軌道を描く記事も書こうと思うので
是非この記事に「スキ」していただけると励みになります
この記事が気に入ったらサポートをしてみませんか?
