
数学を解いたら100万ドル!?
こんにちは。
今回は数学についての話です。
数学と聞いて、何も聞きたくないと言う人もいると思いますが
噛み砕いて解説できたらなと思います。
まず、解いたら100万ドルって、そんな馬鹿な
まず、物理や生物、化学はまだ解明されてないことがあるのは分かるけど、
数学って計算するだけでしょ?って思う人もいるかもしれません。
しかし、今回の問題を見て何一つも問題文の意味がわからないと感じるでしょう。
この100万ドルの問題はミレニアム懸賞問題と呼ばれ、アメリカのクレイ数学研究所が選んだ数学における7つの未解決問題です。
問題のタイトルは、次の7つです
ヤン-ミルズ方程式と質量ギャップ問題
リーマン予想
P≠NP予想
NS方程式の会の存在と滑らかさ
ホッジ予想
ポアンカレ予想
バーチ・スウィンナートン-ダイヤー予想(BSD予想)
今回は、そのうちの「リーマン予想」と「ポアンカレ予想」の二つを紹介します。
①リーマン予想
リーマンゼータ関数の全ての非自明な零点の実部は1/2である。
リーマンゼータ関数
リーマンゼータ関数とは、次のような関数です。

複素数と実部
普通に生きている限り、同じ数同士をかけると0以上になる値しか知らないと思いますが、同じ数同士をかけると0未満の値になるものがあります。
具体例を示すと以下のようなものです。
3×3=9 (-4)×(-4)=16 →このような値は実数と呼ばれます
同じ数字をかけて-1になる数をiと定義して
i×i=-1 5i×5i=-25 →このような値は虚数と呼ばれます
複素数とは、実数から虚数を足し引きした数です。
つまり、次のような数が複素数です。
3+2i 5-6i
※「3+2i」の「3」を実部と言い、「2i」を虚部と言います。
「非自明な」と「零点」
「零点」とは、関数が0になるときの変数の値です。
例えば、
2x-6の零点は、x=3です。
「自明な」とは「簡単に分かる」と認識してください。
つまり非自明な零点とは
「関数の値をゼロにする変数のうち見つけることが難しいもの」
ということです。
リーマンゼータ関数の自明な零点とは、-2,-4,-6…のような負の偶数です。

複素数の実部をReとした時、
Re(s)>1の時のみ負の偶数が零点になります。
実際にs=-2を代入すると∞に発散して、絶対に0になりません。
しかし、「解析接続」することで0になります。
ちなみに私は「解析接続」は全くわかりません。
チャレンジャーな方は、以下のURLで参照してみてください。
リーマン予想を簡潔に言い換えると

「ζ(s)の値がゼロとなるときのsの値のうち見つけることが難しいものは、1/2+○iで表される」
という予想です。
リーマン予想が証明できたら何が嬉しいの?
今まで謎に満ち溢れていた「素数」への理解が進むと言われています。

これを変形すると、次のようになります。
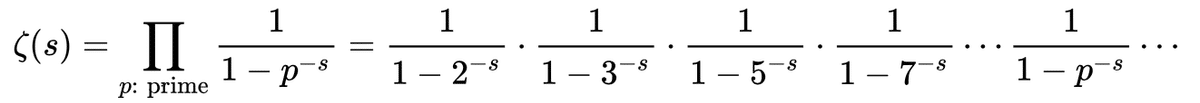
全ての自然数と全ての素数の関係を表しているとい関数です。
素数の個数とリーマンゼータ関数の非自明な零点は密接に関わっています。
リーマン予想が証明できたら、ある範囲にどのくらい素数が存在するのか分かります。
ちなみに、現在10兆個の零点に関しては実部が1/2であることが証明されています。
②ポアンカレ予想
実は、このミレニアム懸賞問題は唯一解決された問題です。
ロシア出身のペレルマン(現在55歳)によって解決されました。
彼の実績は、数学のノーベル賞と言われるフィールズ賞の受賞を辞退、ミレニアム賞である100万ドルの授与を断りました。
それではポアンカレ予想とはどんなものか見てみましょう。
単連結な3次元閉多様体は3次元球面S^3に同相である。
※S^3とはSの3乗と読みます。
単連結
単連結とは図形に輪をかけた時に図形から離れることなく、その輪を一点にまとめることができる性質です。


3次元閉多様体とは
多様体とは、局所的に座標を書き込むことができるような図形
→好きなところに地図を作ることができるような図形
閉とは限定されたという意味です。
つまり、3次元閉多様体とは
「どこでも立体的な地図を書くことができる有限な図形」
です。
3次元球面
n次元球面とは、n+1個の軸からなるn+1次元空間において、原点から等距離にある点の集合体。

3次元球面とは、4次元であり視覚的認識は難しい。
簡単にイメージを付けてもらうと
点(ゼロ次元球面)を細かく打っていくと、円(一次元球面)になります。言い換えると、円は点の連続する図形です。
次に、直径の異なる円(一次元球面)を綺麗に組み合わせていくと球(2次元球面)になります。言い換えると、球を際限なく切っていくと円の組み合わせになります。
てことは、三次元球面とは、際限なく球(二次元球面)を組み合わせた図形になります。
同相
同相とは二つの位相空間が等しいことです。
簡単にいうと、粘土をコネて同じ形を作ることができるもの。
粘土で考えると
○から□や△を作ることは可能ですよね。
つまり、○は□や△と同相であると言えます。
三次元でも考えてみると
マグカップからドーナツも作ることが可能ですよね。
つまり、マグカップとドーナツも同相であると言えます。
ポアンカレ予想を簡潔に言い換えると
単連結な3次元閉多様体は3次元球面に同相である
⬇️
その図形上で輪をかけた時に、図形から離れることなく一点にまとめることができ、どこでも立体的な地図を描くことができる有限な図形は、粘土のようにコネて変形させていくと、4次元空間座標において原点から距離が等しい点の集合からなる図形に変化させることができる。
ポアンカレ予想から何が分かるのか?
宇宙の形のヒントとなると言われています。
ロケットを走らせて、その軌道上にロープを張り巡らせます。
仮にロケットが一周して戻ってきたとします。
その軌道上のロープをある点で一点にまとめることができた場合、
宇宙の形は単連結であると言えます。
ポワンカレ予想から、単連結ならば、宇宙は大体丸い形をしていると言えます。
この記事が参加している募集
この記事が気に入ったらサポートをしてみませんか?
