
一次変換と座標変換の悩ましい関係
「行列と一次変換」は、かつての高校数学で大きなウェイトを占める項目でした。学習指導要領の改訂で項目ごと姿を消し、その内容を学ぶのは大学初年度相当の「線形代数」等の科目まで持ち越されることになりましたが、最近ではデータサイエンスの必要性が高まり、その基礎となる線形代数が重要視されつつあることを考えると、今後どこかで復活があるかもしれません。
その一次変換(または線形変換とも呼ばれます)にまつわる悩ましい問題を取り上げます。話を分かりやすくするために、かつて高校数学で扱われていた、$${ x y }$$ 平面上の点 $${ (x, y) }$$ を点 $${ (X, Y) }$$ に移す一次変換
$$
\left \{ \begin{array}{l} X = a x + by \\ Y = c x + d y \end{array} \right.
\qquad \qquad \qquad \begin{pmatrix} X \\ Y \end{pmatrix} =
\begin{pmatrix} a & b \\ c & d \end{pmatrix}
\begin{pmatrix} x \\ y \end{pmatrix} \qquad (\bigstar)
$$
($${ a, b, c, d }$$ は定数)を考えます。かつての高校数学の教科書等では $${ X, Y }$$ よりは $${ x', y' }$$ と書かれていることが多かったと思いますが、ここでは記号の見やすさから $${ X, Y }$$ と書くことにします。また、式の簡略化のために
$$
\bm{X} = \begin{pmatrix} X \\ Y \end{pmatrix} ,
\quad \bm{x} = \begin{pmatrix} x \\ y \end{pmatrix} ,
\quad A = \begin{pmatrix} a & b \\ c & d \end{pmatrix}
$$
とおきます。今考えているのは、二次元ベクトル $${ \bm{x} }$$ を二次元ベクトル $${ \bm{X} }$$ に対応させる線形写像で、その対応関係は二次の正方行列 $${ A }$$ により $${ \bm{X} = A \bm{x} }$$ と表される、ということになります。
一次変換の視覚化
この行列 $${ A }$$ で表される一次変換がどのような変換であるか、を視覚的に理解する際に、基本ベクトル(大学レベルの線形代数では標準基底とも呼ばれます)
$$
\bm{e}_x = \begin{pmatrix} 1 \\ 0 \end{pmatrix} , \quad
\bm{e}_y = \begin{pmatrix} 0 \\ 1 \end{pmatrix}
$$
が、この一次変換によって
$$
A \bm{e}_x = \begin{pmatrix} a & b \\ c & d \end{pmatrix}
\begin{pmatrix} 1 \\ 0 \end{pmatrix}
= \begin{pmatrix} a \\ c \end{pmatrix} , \quad
A \bm{e}_y = \begin{pmatrix} a & b \\ c & d \end{pmatrix}
\begin{pmatrix} 0 \\ 1 \end{pmatrix}
= \begin{pmatrix} b \\ d \end{pmatrix}
$$
に移される、ということがよく使われます。このことを図として表すと、下図のようになります:

一次変換をする前は、互いに直交する基本ベクトル $${ \bm{e}_x , \bm{e}_y }$$ によって平面が張られていて、平面上の各点の座標値は正方形の格子状に決まっているのに対し、一次変換をした後は(色々な場合がありますが、一例として)格子が辺の斜交した平行四辺形になるようなイメージです。
この一次変換によって出てきた二つのベクトル $${ A \bm{e}_x }$$ と $${ A \bm{e}_y }$$ が平行な場合は、$${ x y }$$ 平面全体が原点を通る直線に写されることになります。ここでは、平面全体が平面全体に写るような一次変換を考えたいので、$${ A \bm{e}_x }$$ と $${ A \bm{e}_y }$$ が平行となるような場合は除外します。そのための条件は「行列 $${ A }$$ の行列式 $${ \det A }$$ がゼロではない(したがって逆行列 $${ A^{-1} }$$ が存在する)」ということで、以降はそれを前提とします。
一次変換で表される座標変換での座標軸
物理などの、線形代数をよく使う分野において一次変換が出てくるのは、例えば座標変換もしくは変数変換をする際です。もちろん、一般的に座標変換や変数変換が一次変換で表されるとは限りませんが(むしろ一次変換では表せないことの方が多いくらいですが)ここでは一次変換で表されるような座標変換を考えることにします。ローレンツ変換や「回転座標系への変換」などがこれに該当します。
今、ある物理系で式 $${ (\bigstar) }$$ で表されるような座標変換をすることを考えます。今まで $${ x , y }$$ を変数として書かれていた式や物理量を $${ X , Y }$$ という新しい変数で書き換えようとしているわけです。このとき、新しい変数による座標軸である $${ \bm{X} }$$ 軸と $${ \bm{Y} }$$ 軸は $${ \bm{x y} }$$ 平面の中でどのようになるか、ということがこの記事の主題です。
前節で述べた視覚的なイメージから「$${ X }$$ 軸と $${ Y }$$ 軸はそれぞれ $${ A \bm{e}_x }$$ と $${ A \bm{e}_y }$$ の方向になる」という誤解をする人はかなり多いのではないでしょうか?(私もそうでした)
「行列 $${ A }$$ で表される一次変換によって $${ x }$$ 軸と $${ y }$$ 軸は $${ A \bm{e}_x }$$ と $${ A \bm{e}_y }$$ の方向に移される」というのはもちろん正しいですが、それは $${ X }$$ 軸と $${ Y }$$ 軸がその方向になることを意味しません。では、どう考えればよいでしょうか?
例えば $${ x y }$$ 平面において $${ x }$$ 軸というのは「$${ y = 0 }$$ を満たす点の集合」のことです。同様に考えると $${ X }$$ 軸は「$${ Y = 0 }$$ を満たす点の集合」$${ Y }$$ 軸は「$${ X = 0 }$$ を満たす点の集合」となります。すると式 $${ (\bigstar) }$$ から、$${ X }$$ 軸と $${ Y }$$ 軸はそれぞれ $${ x y }$$ 平面において $${ c x + d y = 0 }$$, $${ a x + b y = 0 }$$ という式で表される直線となることが分かります。
これと関係することとして、座標変換の結果、新しい変数となった $${ X , Y }$$ に関する基本ベクトル $${ \bm{u}_X , \bm{u}_Y }$$ を求めてみます。$${ X }$$ 軸と $${ Y }$$ 軸はそれぞれベクトル $${ \bm{u}_X , \bm{u}_Y }$$ の方向となっているはずです。
ベクトル $${ \bm{u}_X , \bm{u}_Y }$$ は基本ベクトルの定義により $${ X Y }$$ 座標系においてそれぞれ $${ \begin{pmatrix} 1 \\ 0 \end{pmatrix} }$$ と $${ \begin{pmatrix} 0 \\ 1 \end{pmatrix} }$$ という成分を持つので、このことから $${ x y }$$ 座標系での成分を求めればよいです。式 $${ (\bigstar) }$$ から、それを求める式は
$$
\begin{pmatrix} 1 \\ 0 \end{pmatrix} =
\begin{pmatrix} a & b \\ c & d \end{pmatrix}
\begin{pmatrix} x \\ y \end{pmatrix} , \qquad
\begin{pmatrix} 0 \\ 1 \end{pmatrix} =
\begin{pmatrix} a & b \\ c & d \end{pmatrix}
\begin{pmatrix} x \\ y \end{pmatrix}
$$
となり、これらをそれぞれ $${ x , y }$$ について解けばよいことになります。よって
$$
\bm{u}_X = A^{-1} \begin{pmatrix} 1 \\ 0 \end{pmatrix}
= \frac{1}{a d - b c} \begin{pmatrix} d \\ -c \end{pmatrix} , \qquad
\bm{u}_Y = A^{-1} \begin{pmatrix} 0 \\ 1 \end{pmatrix}
= \frac{1}{a d - b c} \begin{pmatrix} -b \\ a \end{pmatrix}
$$
となって、確かにそれぞれ直線 $${ c x + d y = 0 }$$ と $${ a x + b y = 0 }$$ に平行です。このようにして「$${ X }$$ 軸と $${ Y }$$ 軸はそれぞれ $${ A^{-1} \bm{e}_x }$$ と $${ A^{-1} \bm{e}_y }$$ の方向になる」というのが正しく、$${ A \bm{e}_x }$$ と $${ A \bm{e}_y }$$ の方向ではない、ということが分かります。
誤解の原因は何か ー 成分と基底の変換則
上記のような誤解はなぜ起きやすいのか、何が原因だったのか、考えてみます。誤解の直接的な原因は、上にも書いた通り
「行列 $${ A }$$ で表される一次変換によって $${ x }$$ 軸と $${ y }$$ 軸はそれぞれ $${ A \bm{e}_x }$$ と $${ A \bm{e}_y }$$ の方向に移される、ということをもって、それらが $${ X }$$ 軸と $${ Y }$$ 軸の方向になる、と誤認した」
ということですが、その背景を詳しく見ていきます。
準備: 基底とベクトルの成分
準備として、一つ用語の説明をします。高校数学で出てくる基本ベクトル
$$
\bm{e}_x = \begin{pmatrix} 1 \\ 0 \end{pmatrix} , \quad
\bm{e}_y = \begin{pmatrix} 0 \\ 1 \end{pmatrix}
$$
の一般化である基底という「ベクトルの集合」が大学レベルの線形代数で出てきます。基本ベクトルを使えば平面上のどんなベクトルでも、その線形結合で表すことができますが、基本ベクトルでなくても一次独立な二つのベクトルで同様のことができます。このように、平面や空間の任意のベクトルを線形結合で表すために必要な、一次独立なベクトルの集合を基底といいます。(より正確な定義は線形代数の教科書を参照してください。入門的な線形代数の教科書はたくさん出版されていますが、個人的に好きなのは、松坂和夫著「線型代数入門」岩波書店 です)
基本ベクトルからなる集合 $${ E = \left \{ \bm{e}_x , \bm{e}_y \right \} }$$ は平面における一種の基底(前々節で書いた標準基底です)ですが、基底はこれだけに限らない、ということです。そして、ある平面ベクトル $${ \bm{V} }$$ を $${ \bm{V} = V_x \bm{e}_x + V_y \bm{e}_y }$$ と表したとき、$${ V_x , V_y }$$ を通常 $${ \bm{V} }$$ の成分といいますが、別の基底 $${ F = \left \{ \bm{f}_1 , \bm{f}_2 \right \} }$$ をとって $${ \bm{V} = v_1 \bm{f}_1 + v_2 \bm{f}_2 }$$ と表すこともできるわけで、この場合は $${ v_1 , v_2 }$$ が $${ \bm{V} }$$ の基底 $${ F }$$ に関する成分、ということになります。
このように基底の取り方は無数にあり、ベクトルの成分というのは基底の取り方によって変わります。そして基底の取り方というのは座標系の取り方ということであり、座標変換とは基底の変換です。しかし高校数学の段階では、成分というのは標準基底 $${ E }$$ に関する成分を指していて、成分で書かれた式は標準基底 $${ E }$$ を取っている前提なのです。例えば一次変換を表す式 $${ (\bigstar) }$$ の第二式:
$$
\begin{pmatrix} X \\ Y \end{pmatrix} =
\begin{pmatrix} a & b \\ c & d \end{pmatrix}
\begin{pmatrix} x \\ y \end{pmatrix}
$$
は基底 $${ E }$$ に関する成分で表した式です。基底を明示的に使って表すと
$$
X \bm{e}_x + Y \bm{e}_y = A \left( x \bm{e}_x + y \bm{e}_y \right)
$$
となります。この式の意味は「基底 $${ E }$$ に関する成分が $${ ( x , y ) }$$ となるベクトルを行列 $${ A }$$ で変換すると、同じ基底での成分が $${ ( X , Y ) }$$ となる」ということですが、これを
$$
X \bm{e}_x + Y \bm{e}_y = x \left( A \bm{e}_x \right) + y \left( A \bm{e}_y \right) \qquad (\heartsuit)
$$
と書き直すと、「基底 $${ E }$$ に関する成分が $${ ( X , Y ) }$$ となるベクトルは、基底 $${ \left \{ A \bm{e}_x , A \bm{e}_y \right \} }$$ では成分が $${ ( x , y ) }$$ となる」と読むこともできます。(下図参照: 緑色の矢印は一次変換による点の移動を表す)

これは、基底を $${ \left \{ \bm{e}_x , \bm{e}_y \right \} }$$ から $${ \left \{ A \bm{e}_x , A \bm{e}_y \right \} }$$ に換えると、それによってベクトルの成分が $${ ( X , Y ) }$$ から $${ ( x , y ) }$$ となる、ということを言っていて、基底の変換則とベクトルの成分の変換則は互いに逆変換の関係になっている、ということが分かります。式 $${ (\heartsuit) }$$ でベクトルの成分を $${ ( x , y ) }$$ から $${ ( X , Y ) }$$ に変換するように見たければ、式 $${ (\heartsuit) }$$ の両辺に $${ A^{-1} }$$ を作用させて
$$
X \left( A^{-1} \bm{e}_x \right) + Y \left( A^{-1} \bm{e}_y \right) = x \bm{e}_x + y \bm{e}_y
$$
とし、$${ \left \{ A^{-1} \bm{e}_x , A^{-1} \bm{e}_y \right \} }$$ を新たな基底 $${ \left \{ \bm{u}_X , \bm{u}_Y \right \} }$$ と見なせばよいわけです。(下図参照)
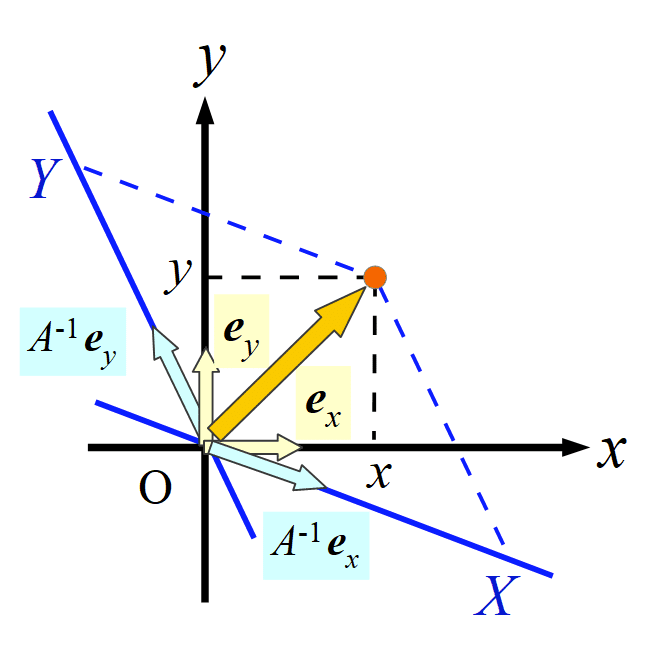
図2は、一次変換の視覚的な理解の仕方として書いた図1右に、変換前後の成分の値などを書き込んだものですが、この図2は変換前の点の座標値 $${ x , y }$$ と変換後の点の座標値 $${ X , Y }$$ の対応関係を標準基底 $${ E }$$ がつくる座標系の中で書いた、というだけで、変換後の座標軸である $${ X }$$ 軸と $${ Y }$$ 軸について何か示しているわけではないです。$${ X }$$ 軸, $${ Y }$$ 軸を何か図で示すには図3のように、変換後の基底が作る軸上に座標値 $${ X , Y }$$ が示されているようなものでなければならないのです。あえて言うと、$${ x }$$ 軸と $${ y }$$ 軸をそれぞれ $${ A \bm{e}_x }$$ と $${ A \bm{e}_y }$$ の方向にとって、それを $${ x y }$$ 座標系であると考えたとき、元の $${ x }$$ 軸と $${ y }$$ 軸が $${ X }$$ 軸と $${ Y }$$ 軸になる、ということはできます。ただ、それよりは図3を見た方が分かりやすいでしょう。
そもそも一次変換は二つのベクトル $${ \bm{x} }$$ と $${ \bm{X} }$$ の対応関係を定めているだけで(それに関わる数学的な知見を座標変換に応用することはできるものの)座標変換を念頭においているわけではないです。それに対して座標変換とは前にも述べた通り、ある座標系で書かれている式や物理量を別の座標系でのものに書き換えをする、ということです。その式や物理量がベクトルで表される場合、座標変換によってその成分は変わりますが、式や物理量それ自体が変わるわけではありません。上の図3は $${ \bm{x} = x \bm{e}_x + y \bm{e}_y }$$ というベクトルが $${ \bm{u}_X = A^{-1} \bm{e}_x }$$, $${ \bm{u}_Y = A^{-1} \bm{e}_y }$$ という基底の変換で決まる座標変換によって $${ \bm{x} = X \bm{u}_X + Y \bm{u}_Y }$$ となることを示しています。
注意: 基底の変換を表す式について
上では、標準基底 $${ E = \left \{ \bm{e}_x , \bm{e}_y \right \} }$$ を行列 $${ A }$$ によって変換して得られる基底を $${ \left \{ A \bm{e}_x , A \bm{e}_y \right \} }$$ と書きました。これは言うまでもなく、基底 $${ E }$$ を構成している二つのベクトル $${ \bm{e}_x , \bm{e}_y }$$ のそれぞれに行列 $${ A }$$ を作用させて得られるベクトル $${ A \bm{e}_x , A \bm{e}_y }$$ から成る基底、という意味です。この変換後の基底を $${ \left \{ \bm{f}_x , \bm{f}_y \right \} }$$ として、基底の変換を
$$
\begin{pmatrix} \bm{f}_x \\ \bm{f}_y \end{pmatrix} =
\begin{pmatrix} \hbox{何らかの} \\ \hbox{ 行列 } \end{pmatrix}
\begin{pmatrix} \bm{e}_x \\ \bm{e}_y \end{pmatrix}
$$
と表すことがあります。上の「何らかの行列」は基底の変換行列と呼ばれます。注意してほしいのは、各々のベクトルに対しては $${ \bm{f}_x = A \bm{e}_x }$$ , $${ \bm{f}_y = A \bm{e}_y }$$ ですが、基底の変換行列は $${ \bm{A} }$$ ではない、ということです。なぜなら、
$$
A = \begin{pmatrix} a & b \\ c & d \end{pmatrix}
$$
から $${ A \bm{e}_x = a \bm{e}_x + c \bm{e}_y }$$, $${ A \bm{e}_y = b \bm{e}_x + d \bm{e}_y }$$ であるので、
$$
\begin{pmatrix} \bm{f}_x \\ \bm{f}_y \end{pmatrix} =
\begin{pmatrix} a & c \\ b & d \end{pmatrix}
\begin{pmatrix} \bm{e}_x \\ \bm{e}_y \end{pmatrix} =
A^{\mathrm{T}} \begin{pmatrix} \bm{e}_x \\ \bm{e}_y \end{pmatrix}
$$
となるからです。$${ A^{\mathrm{T}} }$$ は行列 $${ A }$$ の行と列を入れ換えた転置行列を表します。
例: 二次形式の標準形への変換
一次変換で与えられる座標変換の応用例として「二次形式の標準形への変換」があります。二つの変数 $${ x , y }$$ についての二次の同次式
$$
f ( x , y ) = a x^2 + b x y + c y^2
$$
($${ a, b, c }$$ は定数)を $${ x , y }$$ についての二次形式といいます。この二次形式は
$$
f ( x , y ) = \left( x \ \ y\right)
\begin{pmatrix} a & \frac{b}{2} \\ \frac{b}{2} & c \end{pmatrix}
\begin{pmatrix} x \\ y \end{pmatrix}
$$
と表すことができるので、
$$
\bm{x} = \begin{pmatrix} x \\ y \end{pmatrix} ,
\quad \bm{x}^{\mathrm{T}} = \left( x \ \ y \right) ,
\quad B = \begin{pmatrix} a & \frac{b}{2} \\ \frac{b}{2} & c \end{pmatrix}
$$
とおいて
$$
f ( x , y ) = \bm{x}^{\mathrm{T}} B \bm{x}
$$
と表されることがあります。この二次形式を適当な座標変換により
$$
g ( X , Y ) = \alpha X^2 + \beta Y^2
$$
($${ \alpha , \beta }$$ は定数)の形(これを標準形といいます)にすることを二次形式の標準形への変換、または標準化といいます。これを行うためには、行列 $${ B }$$ の固有値と固有ベクトルを求め、それを基に行列 $${ B }$$ の対角化を行います。(行列の固有値、固有ベクトル、対角化についてはこの記事に簡単に書きました)
行列 $${ B }$$ の固有値を $${ \alpha , \beta }$$ とし、それぞれに対応する固有ベクトルを $${ \bm{u}_1 , \bm{u}_2 }$$ とすると
$$
B \bm{u}_1 = \alpha \bm{u}_1 , \quad B \bm{u}_2 = \beta \bm{u}_2
$$
であり、行列 $${ B }$$ が $${ B^{\mathrm{T}} = B }$$ を満たす行列(このような行列を対称行列といいます)であることから、$${ \alpha \ne \beta }$$ のとき $${ \bm{u}_1 }$$ と $${ \bm{u}_2 }$$ は直交することが示されます。
対称行列 $${ B }$$ が相異なる固有値 $${ \alpha , \beta }$$ を持つとき、それぞれに対応する固有ベクトル $${ \bm{u}_1 , \bm{u}_2 }$$ は直交することを示しておきます。二つのベクトルの内積 $${ \bm{u}_1 \cdot \bm{u}_2 }$$ が $${ \bm{u}_1^{\mathrm{T}} \bm{u}_2 }$$ と表されることに注意して
$${ \qquad \quad \alpha \bm{u}_1 \cdot \bm{u}_2 = B \bm{u}_1 \cdot \bm{u}_2 = \left( B \bm{u}_1 \right)^{\mathrm{T}} \bm{u}_2 = \bm{u}_1^{\mathrm{T}} B^{\mathrm{T}} \bm{u}_2 }$$
$${ \qquad \qquad = \bm{u}_1^{\mathrm{T}} B \bm{u}_2 = \bm{u}_1^{\mathrm{T}} \beta \bm{u}_2 = \beta \bm{u}_1 \cdot \bm{u}_2 }$$
となるので $${ ( \alpha - \beta ) \bm{u}_1 \cdot \bm{u}_2 = 0 }$$ となります。$${ \alpha \ne \beta }$$ より $${ \bm{u}_1 \cdot \bm{u}_2 =0 }$$ が示されます。
固有ベクトル $${ \bm{u}_1 , \bm{u}_2 }$$ をそれぞれ大きさ $${ 1 }$$ になるようにとり、それらを列ベクトルとして持つ行列
$$
P = \bigl( \bm{u}_1 \ \ \bm{u}_2 \bigr)
$$
を定義すると $${ P^{-1} = P^{\mathrm{T}} }$$ となります。このような行列を直交行列といいます。ここで $${ \bm{X} = P^{-1} \bm{x} = P^{\mathrm{T}} \bm{x} }$$ となるベクトル $${ \bm{X} = \begin{pmatrix} X \\ Y \end{pmatrix} }$$ を考えると
$$
\bm{x}^{\mathrm{T}} B \bm{x} = \left( P \bm{X} \right)^{\mathrm{T}} B P \bm{X}
= \bm{X}^{\mathrm{T}} P^{\mathrm{T}} B P \bm{X}
= \bm{X}^{\mathrm{T}} P^{-1} B P \bm{X}
$$
となって $${ P^{-1} B P }$$ が対角行列 $${ \begin{pmatrix} \alpha & 0 \\ 0 & \beta \end{pmatrix} }$$ となるので
$$
\bm{x}^{\mathrm{T}} B \bm{x} = \bigl( X \ \ Y \bigr)
\begin{pmatrix} \alpha & 0 \\ 0 & \beta \end{pmatrix}
\begin{pmatrix} X \\ Y \end{pmatrix} = \alpha X^2 + \beta Y^2
$$
と標準形に変換されます。このようにして $${ \bm{X} = P^{-1} \bm{x} }$$ という一次変換で与えられる座標変換により、二次形式の標準形への変換ができるわけですが、この図形的な意味を考えます。
$${ x y }$$ 平面において $${ f ( x , y ) = a x^2 + b x y + c y^2 = \hbox{定数} }$$ という式で表される図形は $${ a , b , c }$$ の値によりますが、例えば楕円になるように選ぶことができます。ただし、このままの式の形では、それがどのような楕円なのかが分かりにくいので、標準形に変換して $${ g ( X , Y ) = \alpha X^2 + \beta Y^2 = \hbox{定数}}$$ という形にすることで、それが楕円であること、またどのような楕円であるかが明白になります。そして標準形に変換するための変数 $${ X , Y }$$ がつくる $${ X }$$ 軸と $${ Y }$$ 軸は、その楕円の長軸・短軸の方向を向いていることになります。

ここで注意したいのは、座標変数の変換の仕方は上で述べた通り
$${ \begin{pmatrix} X \\ Y \end{pmatrix} = P^{-1} \begin{pmatrix} x \\ y \end{pmatrix}}$$ であって $${ \begin{pmatrix} X \\ Y \end{pmatrix} = P \begin{pmatrix} x \\ y \end{pmatrix}}$$ ではない
のです。それは基底の変換の仕方を見ればよく、行列 $${ P }$$ の定義から、変換前後の基底の関係は $${ \bm{u}_1 = P \bm{e}_x }$$, $${ \bm{u}_2 = P \bm{e}_y }$$ となっていて、前節で述べた「基底の変換則とベクトルの成分の変換則は互いに逆変換の関係となっている」ことから理解できます。
二次形式の標準形への変換をするときに、なぜ $${ \bm{X} = P^{-1} \bm{x} }$$ であって、$${ \bm{X} = P \bm{x} }$$ ではないのか。行列 $${ B }$$ を対角化するための都合、と割り切ることはできますが、上記のように図形的な考察を加えれば納得できるのではないかと思います。
この記事が参加している募集
この記事が気に入ったらサポートをしてみませんか?
