
【ドラえもん×高校数学】あの頃の難題、今なら解ける説
※以下は、以前私が執筆した下のページの内容をnoteに移植したものです。
noteで数式を記述する方法が見当たらなかったため、当該ページの画像で 代用しています。
突然ですが皆さん、この問題をご存じですか?

「ただの積分の問題じゃないか」
そう思うのも無理はありません。
この問題自体に深い意味はないのですから。
しかし、わざわざ取り上げるのには理由があります。
この出題が興味深いのです。
というのも、この問題が見られるのはアニメ「ドラえもん」。
「脱出! 恐怖の骨川ハウス」という回の次のシーンです。10年も昔の回になるでしょうか、覚えている方もあまり多くはないと存じますが・・・。
なぜか印象に残る、私の好きな回の1つです。

ひみつ道具によってのび太一行はスネ夫の屋敷に閉じ込められ、脱出するには数々の問題を解かなければならなくなったのですが、早く問題を解かないと徐々に部屋が狭くなっていき、終いには押しつぶされてしまうため、悠長にしている暇などありません。
一行は「みんなで力を合わせてここを出よう」と意気込み、早速問題に取り組みますが、出題された第一問目がこれ。
しずか曰く、「中学生でも分からないと思う」とのこと。
高校生でも(受験生以外で)解ける人は少数かと思われます。
結局、のび太たちは諦めて別の問題に取り組むことになったのですが、この問題、今なら頑張れば解けるのではないかと思うのです。

というわけで、考えてみます。

おや、積分の中に絶対値が入っています。この絶対値は正負を場合分けして外すのが定石ですよね。
つまり、

と
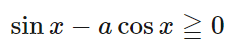
の場合を分けて考えるというコト。
この関数は連続しているので、正負はあるxを境に切り替わります。
したがって、
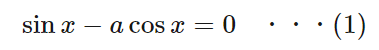
となるxを求めることが重要です。
このxを求めるにはどうすればよいでしょう?
これを考えるためには、まず、aの正負を考える必要があります。
a≦0のときは簡単です。ちょっと考えれば分かりますが、
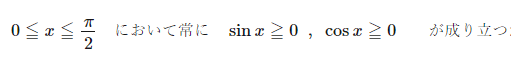
ことを考えると、常に以下が成り立ちます。
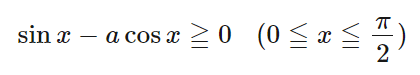
したがって、絶対値はそのまま外すことができて、
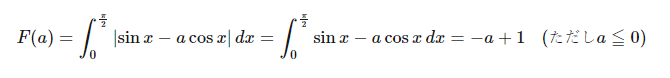
となります。すなわち、a≦0という条件の下ではF(a)の最小値は1です。
これで終わりではありません。a≧0のときも考える必要があります。
a≧0のとき、式(1)の左辺の正負はxの値によって変わります。
どうにかして式(1)の解を求めることはできないでしょうか?
そうです、三角関数の合成の出番ですね。
式(1)は、三角関数の合成により、


と変形することができます。これより、式(1)を満たすxの値は、
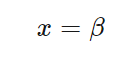
だと分かりますね。
x=βで式(1)の左辺の正負が切り替わるので、

と書くことができて、あとは普通に計算すればよく、

となります。βについては以下のように定義されているのでした。
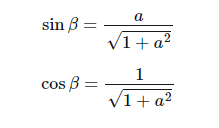
これらを代入して、

と書くことができます。
ここまで来たら、あとはこの関数の最小値を求めるだけです。
この関数の最小値を求めることはさほど難しくはありません。
そうです、aについて微分すればよいですね。
つまり、
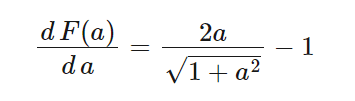
であり、これが0となるときのaの値は、

となります。このときF(a)は極小値をとり、
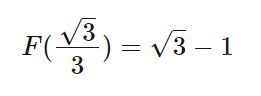
となります。
さて、a≦0のときの最小値は1でした。これと、a≧0のときの最小値√3-1を比べると、後者のほうが小さいので、これが本当の最小値だと分かります。
このときの最小値は
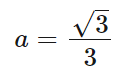
ですね。これが答えです。
これで、無事、スネ夫の部屋から脱出できましたね!

改めて、こちらの記事もご覧ください!
ほかにも、Minecraftや動画編集についてを中心に、様々な記事を執筆しておりますので、よろしければご覧ください。
この記事が参加している募集
この記事が気に入ったらサポートをしてみませんか?
