
オイラーの多面体定理を証明しよう ~数学Aの教科書から姿を消す前に~
オイラーの多面体定理
凸多面体の頂点、辺、面の個数をそれぞれ $${v, e, f}$$ とするとき
$${v-e+f=2}$$ が成り立つ。この値をオイラー数と呼ぶ。
ここで、多面体が凸であるとは
その内部の任意の2点を結ぶ線分が、その多面体の内部にすべて含まれる
ことをいう。
今日は、オイラーの多面体定理を高校生にも理解できるように証明することを目標にします。
具体的には、凸多面体の場合に厳密な証明を与えて、さらに貼り合わせによって複雑な多面体のオイラー数を求める方法を考えます。
実は、僕がこの記事を書く事に決めたきっかけは本定理が高校の数学Aの科目に載っていたことを知ったからです。まずは、そのことからお話したいと思います。
数学Aでの本定理の取り扱い
高校では2022年度から新課程への移行が始まります。それまでは2012年度から続いた旧課程の教科書を使っていたわけですが、今年度から段階的に新課程対応の教科書へと変わっていきます。
僕は旧課程よりもさらに前の教科書を使っていたので知らなかったのですが、旧課程の指導要領では数学Aの多面体の学習内容の中で、オイラーの多面体定理を取り扱うことを例示しているのです。そのため、ほとんどの教科書で本定理を取り扱うことになりました。
一転して、新課程では学習内容が変更されてオイラーの多面体定理への言及が一切なくなりました。教科書を実際に見ていないので分かりませんが、もしかしたらオイラーの多面体定理は教科書から姿を消すかもしれません。
僕は旧課程で本定理がどのように取り扱われたのか気になったので調べてみました。すると、正多面体やそれらの角を取り除いたサッカーボールなどの多面体に対して本定理が成り立つことを、実際に数えて確かめる形式がほとんどでした。
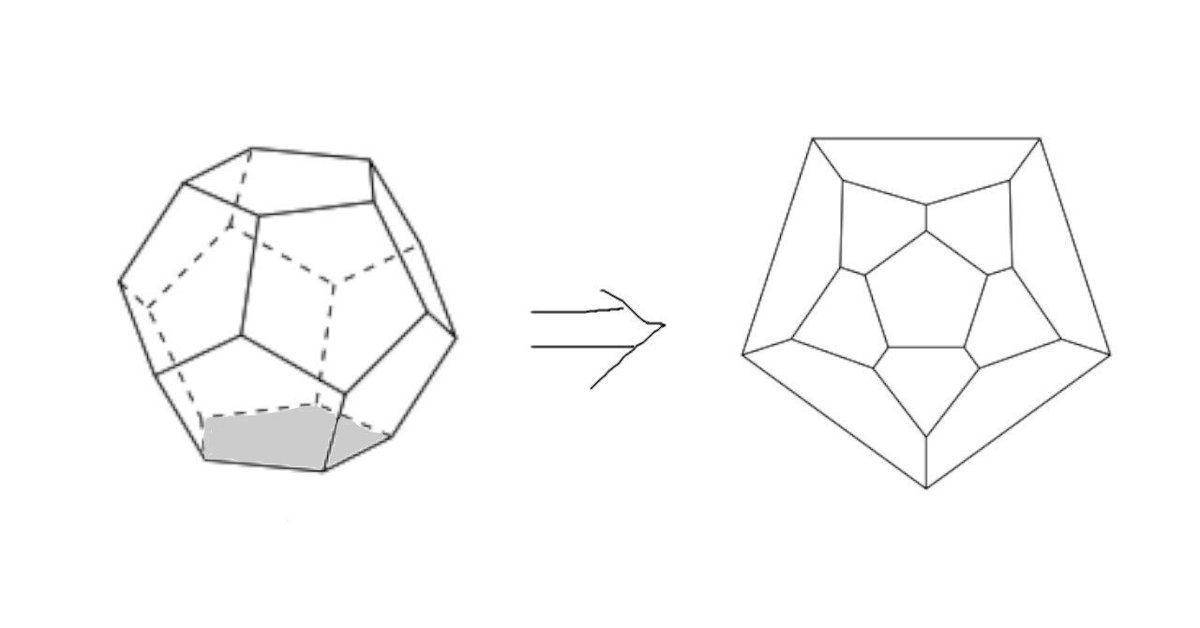
本定理の証明については、多面体から底面を取り除き、残りを引っ張って平面に変形する方法が載っていました。[図1]

ただ、変形の仕方が厳密でなく、僕としては不満が残ります。
実は、凸多面体に限って言えば射影を使って厳密に証明することが可能なのです。そのやり方をこれから紹介したいと思います。
凸多面体の場合の証明
オイラーの多面体定理(再掲)
凸多面体の頂点、辺、面の個数をそれぞれ $${v, e, f}$$ とするとき
$${v-e+f=2}$$ が成り立つ。この値をオイラー数と呼ぶ。
ここで、多面体が凸であるとは
その内部の任意の2点を結ぶ線分が、その多面体の内部にすべて含まれる
ことをいう。
改めて、教科書に載っている証明方法を確認しましょう。
証明方法
まず、凸多面体の底面を一つ取り除きます。
次に、残った面たちを引っ張って、一つの平面図形に変形します。
この平面図形のオイラー数が1であることは容易に分かります。
最初に取り除いた底面1個を合わせると、元の凸多面体のオイラー数が2であることが分かります。
平面図形に変形するのに「引っ張って」と曖昧な言葉を使っているのが問題です。射影を使ってこの問題を解決します。[図2]の右図をご覧ください。
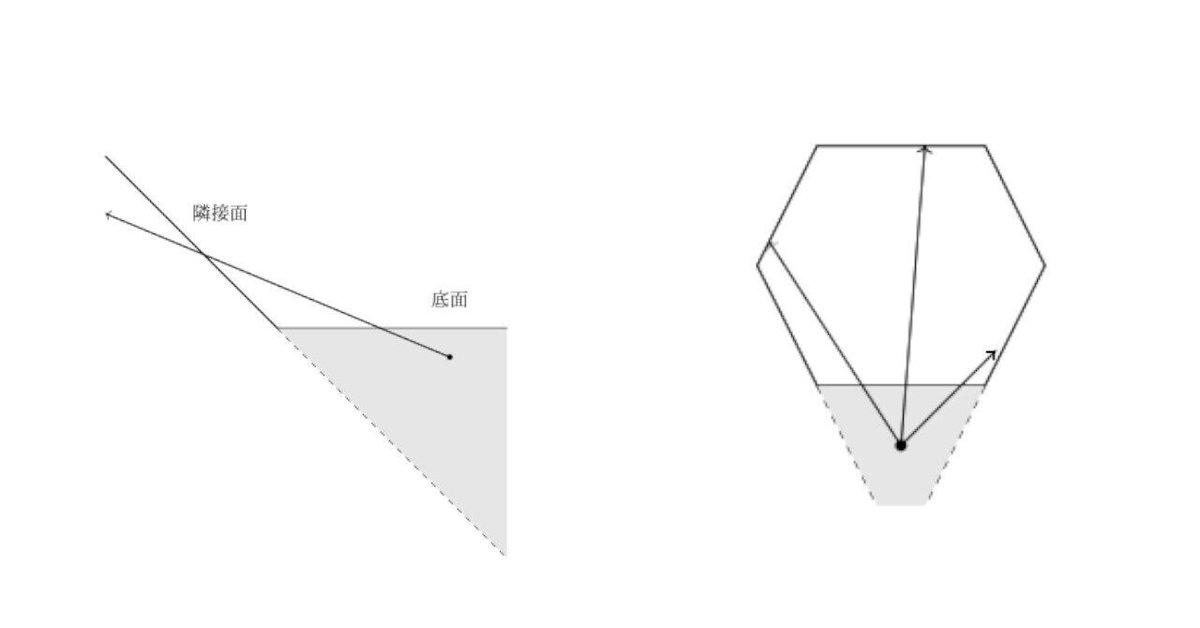
底面の下の丸印を視点として射影します(底面をガラス面にして下から覗き込むと考えると分かりやすいでしょう)。
視点と底面上の任意の1点を結ぶ直線を考えます。この直線が多面体の中から外へ出る点が存在するはずです。さらに、この多面体が凸であることから、一旦外に出た直線が再び多面体の中に入ることはありません。
すなわち、底面上の1点に対して、射影によって多面体の中から外へ出る点がただ一つ対応することが分かります。
次に、[図2]の左図をご覧ください。底面とそれに隣接する面に着目した図です。図の色付き部分に視点を持ってくると、この視点を通り底面と交差するすべての直線が隣接する面とも交差することが分かります。
底面と隣接する面は有限個なので、視点を底面に十分近づけることで、底面内に残りの面たちをすべて射影させることが可能となります。[図2]の右図を再び参照してください。
この射影によって、多角形が多角形に移ること、及び二つの面が隣接するときは射影した先でも隣接することは容易に確認できます。特に頂点、辺、面の数はこの射影によって変わらないことが分かります。
以上によって問題点は解決され、凸多面体の場合の厳密な証明が完結しました。
次に、本定理を凸でない場合に拡張するために、多面体の貼り合わせによってオイラー数がどのように変化するのかを見ていきましょう。
貼り合わせで得られる多面体の場合
二つの多面体を貼り合わせて新しい多面体を作るとき、この新しい多面体のオイラー数を考えてみましょう。
二つの多面体のオイラー数をそれぞれ$${E_1,E_2}$$とし、貼り合わせる面(境界線を含む)のオイラー数を$${D}$$、その境界線のみのオイラー数を$${C}$$とします。このとき、この二つを貼り合わせた多面体のオイラー数$${E}$$は
$$
E=E_1+E_2-2D+C
$$
と表されます。[図3]

この公式を理解するには、いくつかの例に触れてみるのが手っ取り早いと思います。[図4]をご覧ください。
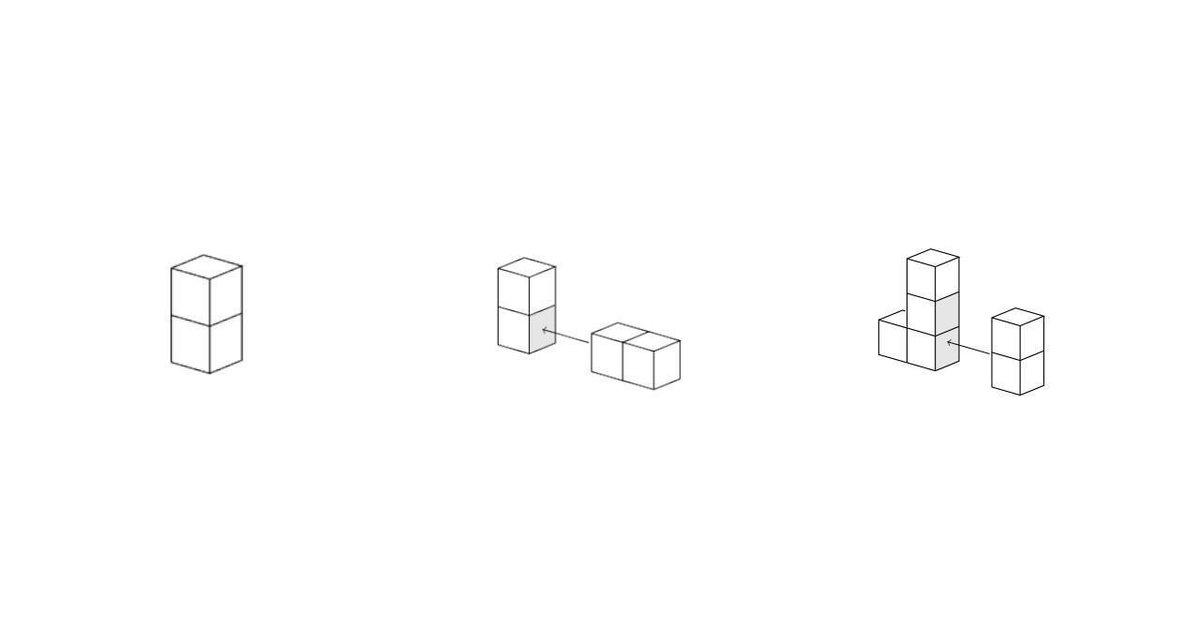
立方体二つを積み上げた左図の立体のオイラー数が2となることはよいでしょう。
この立体を二つ用意して、中図のように貼り合わせてL字を作ります。貼り合わせる面は四角形でそのオイラー数は1、その境界線は一つのループなのでオイラー数は0です。したがって、L字のオイラー数は $${2+2-2\times 1+0=2}$$ となります。
さらに、L字と最初の立体を右図のように貼り合わせましょう。この新しい立体のオイラー数も $${2+2-2\times 1+0=2}$$ となることが分かります。
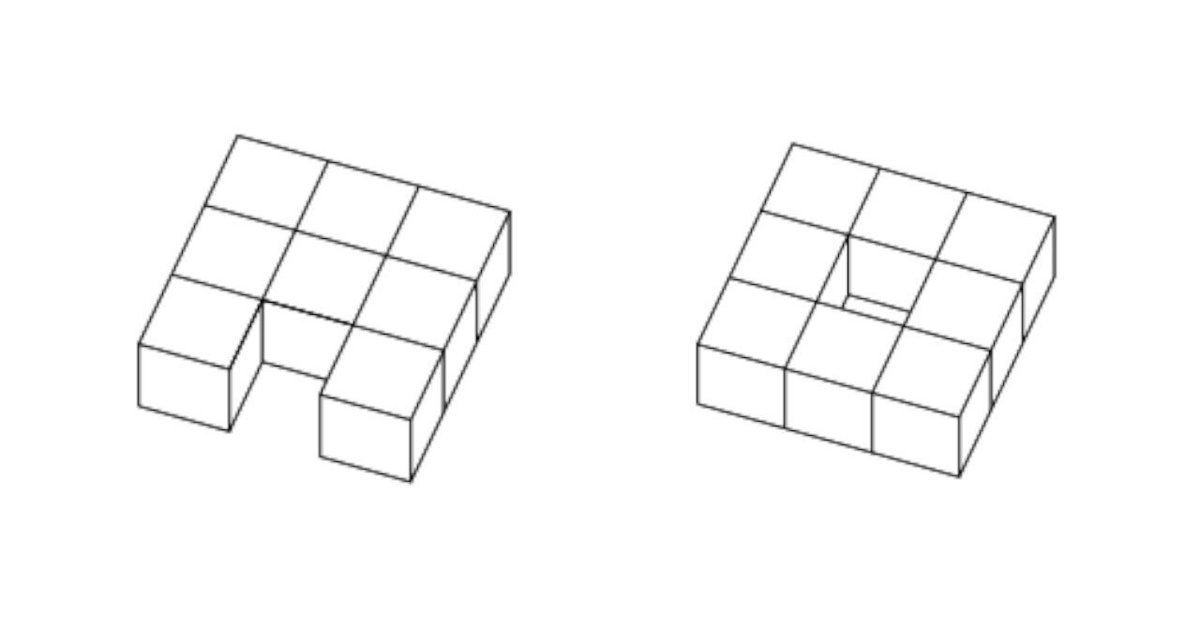
課題として、[図5]の二つの立体のオイラー数をそれぞれ求めてみてください。左図のオイラー数は2、右図は0になるはずです。
いかがだったでしょうか?今日は、オイラーの多面体定理についてお話ししました。
[追記2022/07/18]多面体の貼り合わせについて
上記では、多面体の貼り合わせについて正確な定義をしないまま議論を進めています。これは、角材を使った課題を意識してのことでした。
ただ、公式に一般性を持たせるためには、「多面体の貼り合わせる部分をくり抜いたものを、そのくり抜いた境界線を合わせるように貼り合わせる」と考えたほうがよいと、投稿後に思い至りました。
すなわち、それぞれの多面体から貼り合わせる部分をくり抜いたものを考えると、それらのオイラー数は $${E_1-D+C}$$ 及び$${E_2-D+C}$$ となるのでこれらを境界線を合わせるように貼り合わせた多面体のオイラー数は、境界線部分が重複するので
$$
E=(E_1-D+C)+(E_2-D+C)-C=E_1+E_2-2D+C
$$
となって上記の公式と一致します。
一般に多面体の貼り合わせでは、「貼り合わせ部分が重複するのでそれを引く」という考え方が重要です。今回の場合は、たまたま多面体から一部をくり抜いたものを扱っているにすぎないわけです。
以上、失礼しました。
参考資料
この記事が参加している募集
最後まで記事を読んでいただきありがとうございました!
