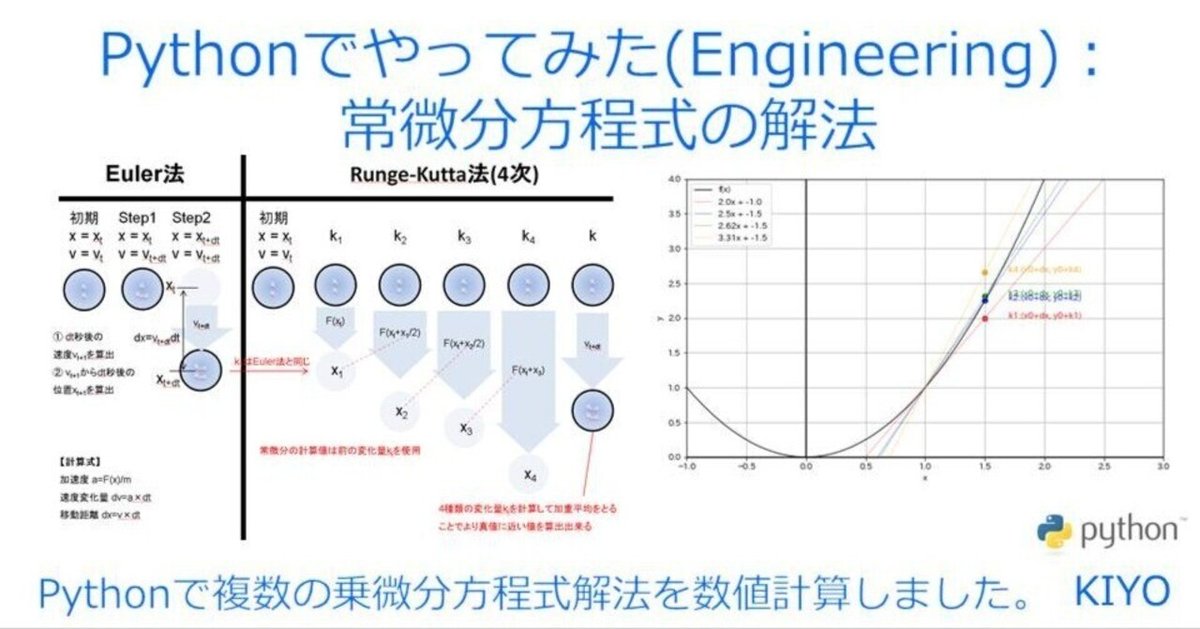
Pythonでやってみた(Engineering):常微分方程式の解法(Euler/Leap-Flog/Runge/Runge-Kutta法)
1.概要
本記事では常微分方程式を数値的に解く手法を紹介します。大前提として微分を数式的に解けるのであれば数値計算を使用しない方がよいです。ただし、多くの問題は数式的には解けないため数値計算で解を解きます。
1ー1.方程式一覧
常微分方程式を解く手法として下記を紹介します。
●Euler法:最もシンプルだが計算精度は低い
●Leap-Frog法:Euler法の時間単位を分割することで精度をあげた
●Runge-Kutta法:精度は高いが数式が複雑であり計算量も多い
1-2.サンプル用問題:物体の自由落下
サンプル問題として「自由落下する物体において100m高さから1kgの物体を落とした時の地表までの速度と時間を算出」します。
物理の方程式は下記を使用します。まずは事前に理論値を算出しました。
U:位置エネルギー[J]、K:運動エネルギー[J]、m:重量[kg]、g:重力加速度[$${m/s^2}$$]、h:高さ[m]、v:速度[m/s](初速$${v_{0}=0}$$)
$$
位置エネルギーU=mgh、運動エネルギーK=\frac{1}{2}mv^2
$$
$$
運動エネルギー K + 位置エネルギー U = 力学的エネルギー E
$$
【理論速度:地面直前の速度】
上記より地表(h=0よりU=0)では位置エネルギーがすべて運動エネルギーに変換されるため$${U=K}$$つまり$${mgh=\frac{1}{2}mv^2}$$より、結果は下記の通りです。
$$
v=\sqrt{2gh}=\sqrt{2×9.80665×100}=44.287m/s
$$
【理論時間:地面到達までの時間】
結論は$${t=\sqrt{\frac{2h}{g}}}$$です。
まず初めに基本式として$${速度v=加速度a×時間t}$$である。よってt秒後の速度vは$${v=gt+v_{0}}$$となる。自由落下では初速$${v_{0}=0}$$のため$${v=gt}$$となる。
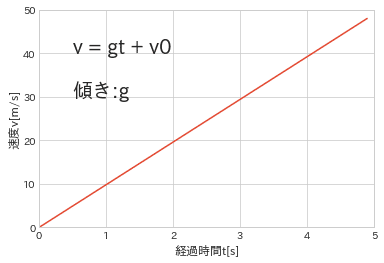
移動距離x=速度v×時間tのため微小時間dtで考えると$${dx=v×dt }$$となりdt後に微小距離dx移動する。上記より$${v=gt}$$のため下記が成り立つ。
$$
dx=v×dt よりdx = gt×dt
$$
上記を積分すると下記となり条件値を当て込むと理論落下時間が得られる。
$$
\int_{0}^{h}dx=\int_{0}^{t}(gt) dtよりh=\frac{1}{2}gt^2
$$
$$
t=\sqrt{\frac{2h}{g}}=\sqrt{\frac{2×100}{9.80665}}=4.516 s
$$
1-3.万有引力と重力加速度の関係
上記の式でg:重力加速度[$${m/s^2}$$]を使用しましたが、このgは地球の質力と落下させる物体の距離から発生する万有引力に起因します。
【物理定数・地球の物性】
●万有引力定数G:$${6.67430×10^{11} ~m^3kg^{-1}m^{-2}}$$
●地球の半径r:6,378,136 m
●地球の質量M:$${ 5.972×10^{24}~kg}$$
※上記の数値をそのまま使用すると地表面での重力加速度gが9.80665にならないため、計算上では微調整した数値を使用しました。
※上式のmは落下させる物体の質量[kg]です。
$$
万有引力F=G\frac{Mm}{r^2}
$$
$$
力と加速度の関係:F=ma
$$
$$
物体にかかる加速度※:a=\frac{F}{m}=G\frac{Mm}{mr^2}=G\frac{M}{r^2}
$$
※通常使用する重力加速度gと同じだが地球からの距離rによって加速度aが変化する。よって加速度は説明変数rの関数f(r)となる。
※rは2物体間の距離のためr=地球の半径+物体の地表面からの高さとなる。
[IN]
G = 6.6743e-11 #万有引力定数
r_earth = 6.378136*10**6 #地球の半径[m]
M = 5.972*10**24 #地球の質量[kg]※出典:Wikipedia
M_adjust = 5.977264892098201*10**24 #地球の質量[kg]※重力加速度に合うように調整
grav_acceralation = G*M/(r_earth**2) #地球の重力加速度[m/s^2]
grav_acceralation_adjust = G*M_adjust/(r_earth**2) #地球の重力加速度[m/s^2]
print(grav_acceralation)
print(grav_acceralation_adjust)
[OUT]
9.79801211042561
9.806651-4.計算の初期条件/関数:Pythonコード
コードを記載していきます。機能ごとに項を分けて説明します。
1-4-1.初期条件の設定
サンプル問題の初期条件は下記で計算してきます。
【計算条件】
●質量:1.0kg ※自由落下では質量は計算結果に影響は与えません
●高さ:100m
●刻み幅h(微小時間):10ms
●初速度v0:0m/s (100mのところからそっと手を放すイメージ)
[IN]
#計算条件
g = 9.80665 #重力加速度
mass = 1.0 #質量
height = 100 #高さ
dt=0.01 #時間刻み[sec]
force = mass*g #重力
#初期条件
time = 0.0 #動作時間[s]
v0=0.0 #速度の初期値[m/s]
#Data格納用
datas = {'time':[],
'height':[],
'velocity':[]}
#初期データ登録
datas['time'].append(time)
datas['height'].append(height)
datas['velocity'].append(v0)
print(datas)
[OUT]
{'time': [0.0], 'height': [100], 'velocity': [0.0]}1-4-2.取得データの保存用クラス
微小時間dtごとの①経過時間t、②地表面からの高さh, ③物体の速度を保存するクラスを作成します。機能は下記の通りです。
データの保存(リストに追加):クラス内のリストのデータを追加※Callメソッドのため属性名は記載せず使用できる
データの初期化:使いまわしできるようリストデータを空にする
データの出力:各データをまとめて出力する機能->PandasでDataFrame化できるように辞書型で出力
[IN]
#Data格納用
class DataLogger:
def __init__(self):
self.time = []
self.height = []
self.velocity = []
def __call__(self, t, h, v):
self.time.append(t)
self.height.append(h)
self.velocity.append(v)
def reset(self):
self.time = []
self.height = []
self.velocity = []
def output(self):
datas = {'time': self.time, 'height': self.height, 'velocity': self.velocity}
return datas
datas = DataLogger()
print(datas.output()) #初期状態の確認
t, h, v = 0, 1, 2
datas(t=t, h=h, v=v) #データの追加
print(datas.output()) #追加後の確認
datas.reset() #データのリセット
print(datas.output()) #リセット後の確認
[OUT]
{'time': [], 'height': [], 'velocity': []}
{'time': [0], 'height': [1], 'velocity': [2]}
{'time': [], 'height': [], 'velocity': []}1-4-3.万有引力のクラス化
地表面に行くほど力(重力)がかかるため高さを力の要因とする関数を作成します。
[IN]
def universal_grav(m, height):
G = 6.6743e-11 #万有引力定数
r_earth = 6.378136*10**6 #地球の半径[m]
r = r_earth + height #地球中心からの距離[m]
M = 5.977264892098201*10**24 #地球の質量[kg]※重力加速度に合うように計算
force = G*M*m/r**2 #万有引力
return force
print(universal_grav(1,0)) #m=1kg, F=maから重量加速度gと同じ
print(universal_grav(1,100)) #m=1kg, F=maから重量加速度gと同じ
[OUT]
9.80665
9.806342498893923地表(h=0m)と初期(h=100m)ではかかる力が変わることが確認できました。ただ地球の半径が$${10^6}$$オーダーのため影響は微小です。
1-4-4.可視化:アニメーション作成
時間ごとの物体の変化が分かるようにAnimationを作成してGif化できる関数を作成しました。作成要領は下記記事を参照ください。
(※このタイミングで実行してもエラーとなるため参考用です)
[IN]
def plot_fallingobj(frame_No):
output = datas.output()
plt.cla()
plt.xlim(-1, 1); plt.ylim(0, 100)
plt.grid()
height = np.array(output['height'])[frame_No] #特定フレーム(時間)の高さ
x = [0] #x軸:中央に配置
im = plt.scatter(x, height, s=100, c='r')
#テキスト表示
v = output['velocity'][frame_No]
time = output['time'][frame_No]
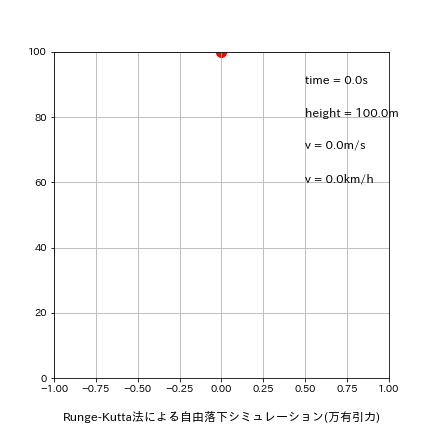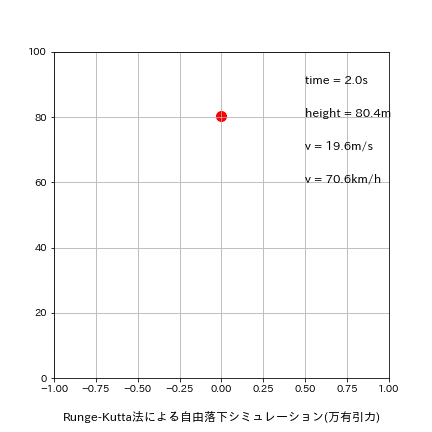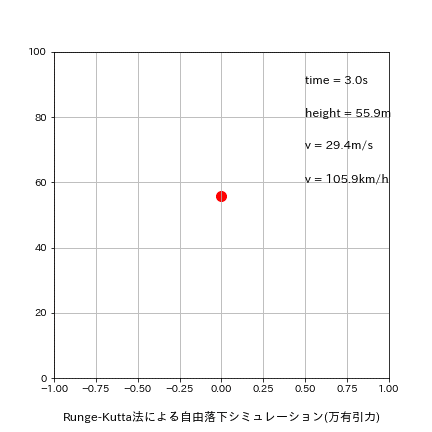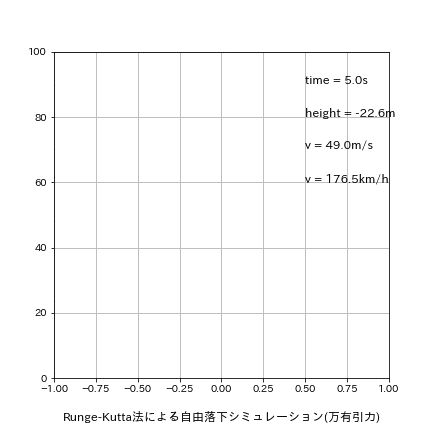
plt.text(0.5, 90, f'time = {round(time,1)}s', fontsize=12)
plt.text(0.5, 80, f'height = {round(height,1)}m', fontsize=12)
plt.text(0.5, 70, f'v = {round(v,1)}m/s', fontsize=12)
plt.text(0.5, 60, f'v = {round(v*3600/1000,1)}km/h', fontsize=12)
fig = plt.figure(figsize=(6,6),facecolor='white')
plt.grid()
ani = animation.FuncAnimation(fig, plot_fallingobj, interval=150, frames=len(datas.time))
ani.save('Euler/Euler.gif', writer='pillow')
HTML(ani.to_html5_video())
[OUT]
出力イメージは下図の通り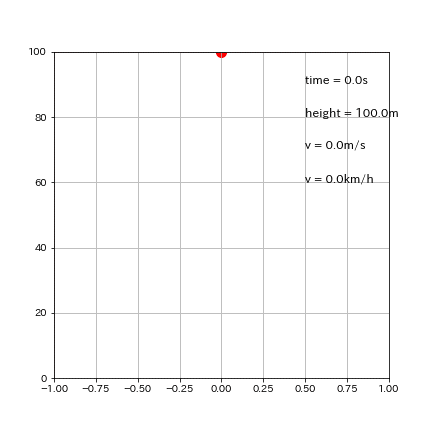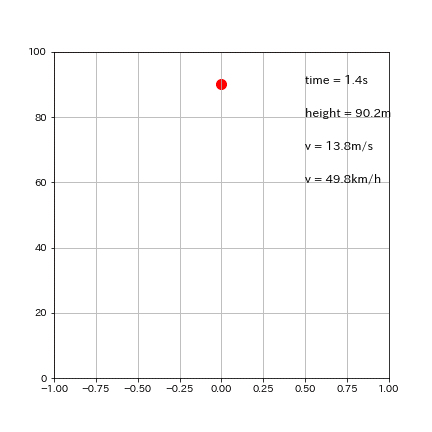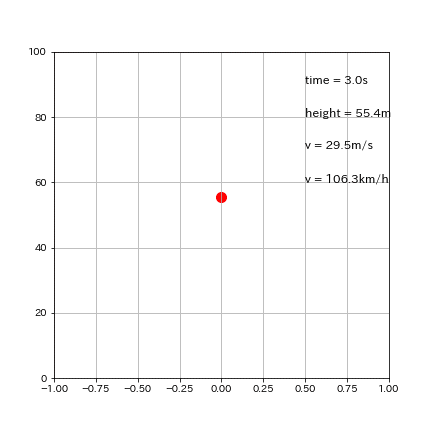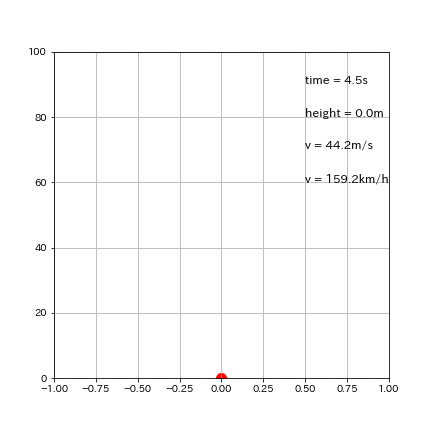
2.Euler法(オイラー法)
2-1.数式の理解
オイラー法は最もシンプルな方法であり下記特徴があります。
$$
Euler法:f(x+dx) = f(x) + f'(x)dx
$$
【Euler法の特徴】
●微小変化dx(刻み幅h)においてf(x)の傾きが変わらないとして、微小変化量hから求めたいf(x)の微小変化を求める。
●hを逐次的に進めていくことでf(x)が微小に変化していくため、求めたい値xにおける数値が計算できる。
U:位置エネルギー[J]、K:運動エネルギー[J]、m:重量[kg]、g:重力加速度[$${m/s^2}$$]、a:加速度[$${m/s^2}$$]、h:高さ[m]、v:速度[m/s](初速$${v_{0}=0}$$)
【速度変化】
力Fを地球からの距離xとの関数f(x)とするとdt後の速度vは下記の通りです。
$$
加速度a=\frac{dv}{dt}、力の公式F=maより\frac{dv}{dt}=\frac{F}{m}
$$
$$
dv = \frac{f(x)}{m}dtより\\
v_{t+dt}=v_{t}+ \frac{f(x)}{m}dt
$$
【移動距離変化】
$$
v=\frac{dx}{dt}よりdx=vdt \\
x_{t+dt}=x_{t}+vdt
$$
2-2.Pythonコード(関数化)
2-2-1.メイン関数
オイラー法をコード化するためクラス化して機能は下記の通りです。
初期化(インスタンス作成時)に微小時間dtを渡す。
機能として①万有引力による速度変化dvからdt後の速度、②速度からの移動距離dxからdt後の高さh を出力できます。
高さhの変化->万有引力の変化(つまり加速度の変化)->速度変化のようにstep(dt秒ごと)に各数値が変化していきます(固定値の重力加速度gは不使用)。
[IN]
#Euler法
class Eulermethod:
def __init__(self, dt):
self.dt = dt
def step_velocity(self, v, force, mass):
v_next = v + (force/mass)*self.dt #vt+1 = vt + (F/m)*dt
return v_next
def step_height(self, h, v):
h_next = h - v*self.dt #ht+1 = ht - vt*dt 落下のため移動距離はマイナス
return h_next2-2-2.シミュレーション
シミュレーションは下記を繰り返し計算するだけです。計算の収束条件は自分で決める必要があるため移動距離が100m(地面に到着)したら終了する用にループを決めました。
現在の位置(高さ)から重力(万有引力)forceを計算(加速度の算出用)
微小時間dt後の速度vをEuler法(step_velocity)で算出
微小時間dt後の高さheightをEuler法(step_height)で算出
#計算条件
g = 9.80665 #重力加速度
mass = 1.0 #質量
height = 100 #高さ
dt=0.01 #時間刻み[sec]
force = mass*g #重力
#初期条件
time = 0.0 #動作時間[s]
v0=0.0 #速度の初期値[m/s]
datas = DataLogger()
datas(time, height, v0) #初期値を格納
euler = Eulermethod(dt)
count = 0
v = v0 #初速度
while 0<=height:
force = universal_grav(mass, height) #現在の位置での万有引力
v_next = euler.step_velocity(v, force, mass) #v_next = v + (F/m)*dt
height = euler.step_height(height, v_next)
v = v_next #vを更新
time += dt #時間を更新
#データ追加:100msごと+最後の1回
if count%10==0 or height<=0:
datas(time, height, v) #データを格納
count += 1
output = datas.output()
print(f'落下地点での結果 t={output["time"][-1]:.3f}s, h={output["height"][-1]:.2f}[m], v={output["velocity"][-1]:.3f}[m/s]')
[OUT]
落下地点での結果 t=4.520s, h=-0.40[m], v=44.325[m/s] 結果としてEuler法では(理論time:4.516s、理論v:44.287m/s)を比較的良い精度で計算できております。
今回は簡単な関数のため精度が高いですがより複雑になると後述するRunge-Kutta法が必要になります。
[IN]
fig = plt.figure(figsize=(6,6), facecolor='white')
x, y = np.array(output['time']), np.array(output['height'])
plt.plot(x,y)
plt.xlabel('経過時間t[s]'); plt.ylabel('高さh[m]'); plt.grid()
plt.show()
[OUT]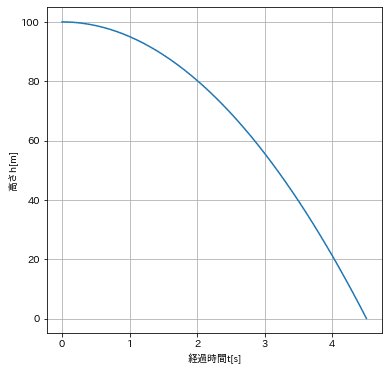
[IN]
def plot_fallingobj(frame_No):
output = datas.output()
plt.cla()
plt.xlim(-1, 1); plt.ylim(0, 100)
plt.grid()
height = np.array(output['height'])[frame_No] #特定フレーム(時間)の高さ
x = [0] #x軸:中央に配置
im = plt.scatter(x, height, s=100, c='r')
#テキスト表示
v = output['velocity'][frame_No]
time = output['time'][frame_No]
plt.text(0.5, 90, f'time = {round(time,1)}s', fontsize=12)
plt.text(0.5, 80, f'height = {round(height,1)}m', fontsize=12)
plt.text(0.5, 70, f'v = {round(v,1)}m/s', fontsize=12)
plt.text(0.5, 60, f'v = {round(v*3600/1000,1)}km/h', fontsize=12)
plt.title('Euler法による自由落下シミュレーション(万有引力)', y=-0.15)
fig = plt.figure(figsize=(6,6),facecolor='white')
plt.grid()
ani = animation.FuncAnimation(fig, plot_fallingobj, interval=150, frames=len(datas.time))
ani.save('Euler/Euler.gif', writer='pillow')
HTML(ani.to_html5_video())
[OUT]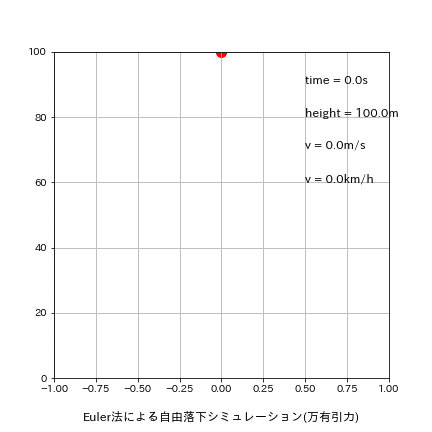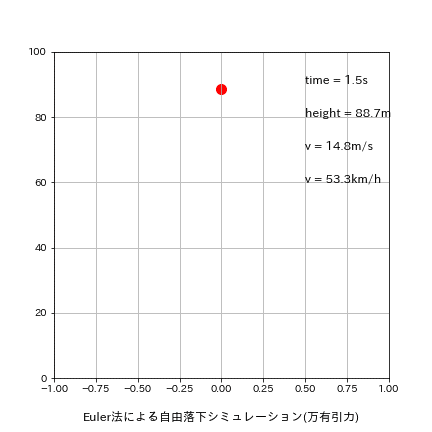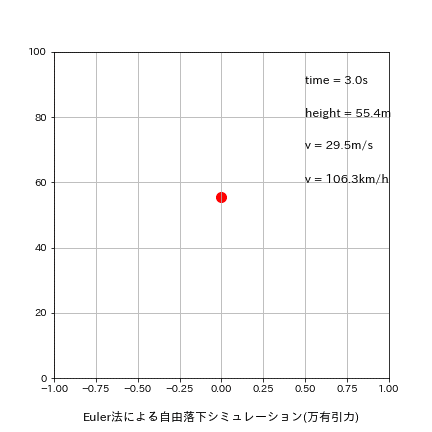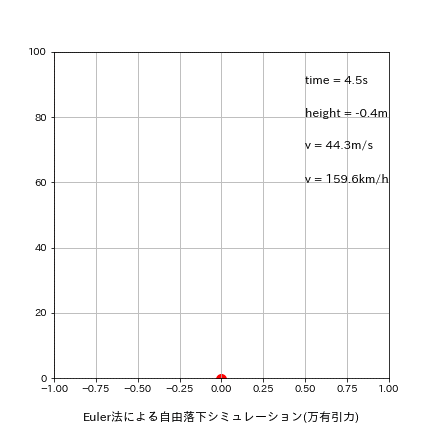
3.Leap-Frog法
3-1.数式の理解
Euler法の欠点は微小区間(刻み幅)dtの間で計算に補正できない点です。
例として下記万有引力の例だと微小時間dtで物体が移動する間に移動後の位置(変化量)が次の移動量(移動速度)に影響を与えます(重力(加速度)変化->速度変化->位置変化の繰り返し)
よってdtの間で変化量に影響を与える要因が変化しているにも関わらず、その変化を補正することが出来ません。
$$
Euler法:f(x+dx) = f(x) + f'(x)dx
$$
Leap-Frog法では微小変化を半分:$${\frac{dt}{2}}$$して、最初の$${\frac{1}{2}}$$の変化で結果に影響する要因を更新して、残りの$${\frac{1}{2}}$$で更新した要因を引数に結果を再更新します。
$$
Leap-Frog法\\
f_{mid} = f(x) + f'(x)\frac{dx}{2} \\
x_{x+dx}=x+f_{mid}dx \\
f_{x+dx} = f_{mid}+f'(x_{x+dx})\frac{dx}{2}
$$
$$
Leap-Frog法(万有引力の場合)\\
v_{mid} = v_{t} + \frac{f(x)}{m}\frac{dt}{2} \\
x_{t+dt}=x_{t}+v_{mid}dt \\
v_{t+dt} = v_{mid}+\frac{f(x_{t+dt})}{m}\frac{dt}{2}
$$

3-2.Pythonコード(関数化)
3-2-1.メイン関数
Leap-Frog法をコード化するためクラス化して機能は下記の通りです。
初期化(インスタンス作成時)に①微小時間dtと②位置heightから万有引力を計算できる関数 を渡す。
機能として①万有引力による速度変化dvからdt後の速度、②速度からの移動距離dxからdt後の高さh を出力できます。
位置変化:step_height()は速度変化中に計算する中間速度$${v_{mid}}$$を使用するため直接関数化が難しいです。よって、高さ計算用と出力用の2つに分けました。
高さhの変化->万有引力の変化(つまり加速度の変化)->速度変化のようにstep(dt秒ごと)に各数値が変化していきます(固定値の重力加速度gは不使用)。
[IN]
#Leap-Frog法
class LeapFrogmethod:
def __init__(self, dt, func_force):
self.dt = dt
self.dt_half = dt/2 #Leap-Frog法のために1/2の時間刻みを用意
self.func_force = func_force #万有引力計算用関数
self.h_next = None #出力用
def step_velocity(self, v, height, mass):
force_init = self.func_force(mass, height) #位置heightでの万有引力
v_half = v + (force_init/mass)*self.dt_half
self.h_next = self._step_height(height, v_half) #dt秒後の高さ
force_next = self.func_force(mass, self.h_next) #dt秒後の万有引力
v_next = v_half + (force_next/mass)*self.dt_half
return v_next
def _step_height(self, h, v):
h_next = h - v*self.dt #ht+1 = ht - vt*dt 落下のため移動距離はマイナス
return h_next
def step_height(self):
if self.h_next is None:
raise ValueError('h_next is None. Please execute step_velocity() first.')
else:
return self.h_next
[OUT]3-2-2.シミュレーション
シミュレーションは下記を繰り返し計算するだけです。計算の収束条件は自分で決める必要があるため移動距離が100m(地面に到着)したら終了する用にループを決めました。
現在の位置(高さ)から重力(万有引力)forceを計算(加速度の算出用)
微小時間dt後の速度vをLeap-Frog法(step_velocity)で算出
微小時間dt後の高さheightをLeap-Frog法(step_height)で算出(step_velocityで計算した値を変数に格納してほしい時に出力)
[IN]
#計算条件
g = 9.80665 #重力加速度
mass = 1.0 #質量
height = 100 #高さ
dt=0.01 #時間刻み[sec]
force = mass*g #重力
#初期条件
time = 0.0 #動作時間[s]
v0=0.0 #速度の初期値[m/s]
#Data格納用
datas.reset() #データの初期化
datas(time, height, v0) #初期値を格納
#Leap-Frog法
leapfrog = LeapFrogmethod(dt, universal_grav)
count = 0
v = v0 #初速度
while 0<=height:
force = universal_grav(mass, height) #現在の位置での万有引力
v_next = leapfrog.step_velocity(v, height, mass)
height = leapfrog.step_height()
v = v_next #vを更新
time += dt #時間を更新
#データ追加:100msごと+最後の1回
if count%10==0 or height<=0:
datas(time, height, v) #データを格納
count += 1
output = datas.output()
print(f'落下地点での結果 t={output["time"][-1]:.3f}s, h={output["height"][-1]:.2f}[m], v={output["velocity"][-1]:.3f}[m/s]')
[OUT]
落下地点での結果 t=4.520s, h=-0.17[m], v=44.325[m/s] 結果としてEuler法と同じ時間・速度になりました(処理完了時の位置はより地表に近くなった)。理由として地球の半径が$${10^6}$$オーダーのため高さheightの影響は0.01%程度の影響しかないためです。
参考用にアニメーションも作成しました。
[IN]
def plot_fallingobj(frame_No):
output = datas.output()
plt.cla()
plt.xlim(-1, 1); plt.ylim(0, 100)
plt.grid()
height = np.array(output['height'])[frame_No] #特定フレーム(時間)の高さ
x = [0] #x軸:中央に配置
im = plt.scatter(x, height, s=100, c='r')
#テキスト表示
v = output['velocity'][frame_No]
time = output['time'][frame_No]
plt.text(0.5, 90, f'time = {round(time,1)}s', fontsize=12)
plt.text(0.5, 80, f'height = {round(height,1)}m', fontsize=12)
plt.text(0.5, 70, f'v = {round(v,1)}m/s', fontsize=12)
plt.text(0.5, 60, f'v = {round(v*3600/1000,1)}km/h', fontsize=12)
plt.title('Leap-Frog法による自由落下シミュレーション(万有引力)', y=-0.15)
fig = plt.figure(figsize=(6,6),facecolor='white')
plt.grid()
ani = animation.FuncAnimation(fig, plot_fallingobj, interval=150, frames=len(datas.time))
ani.save('LeapFrog/leapfrog.gif', writer='pillow')
HTML(ani.to_html5_video())
[OUT]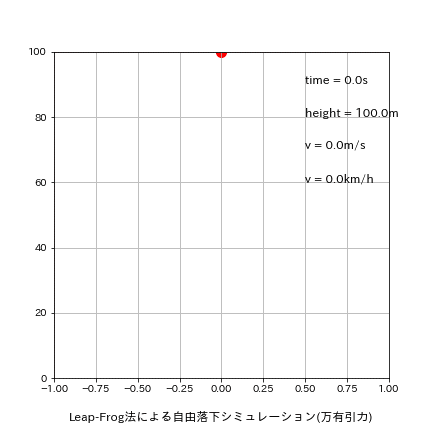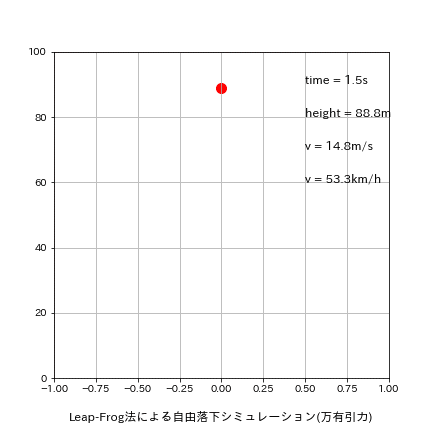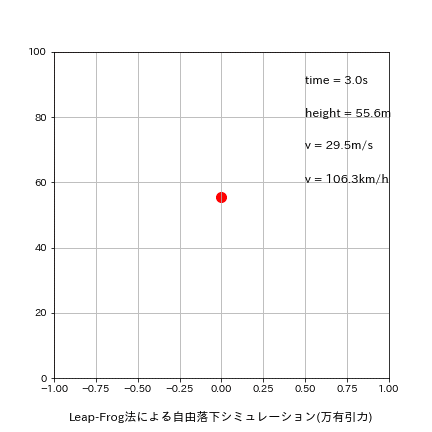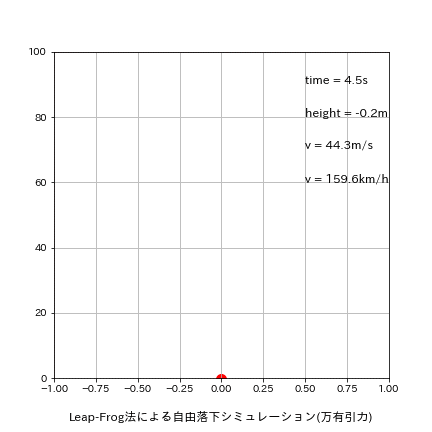
4.Runge-Kutta法
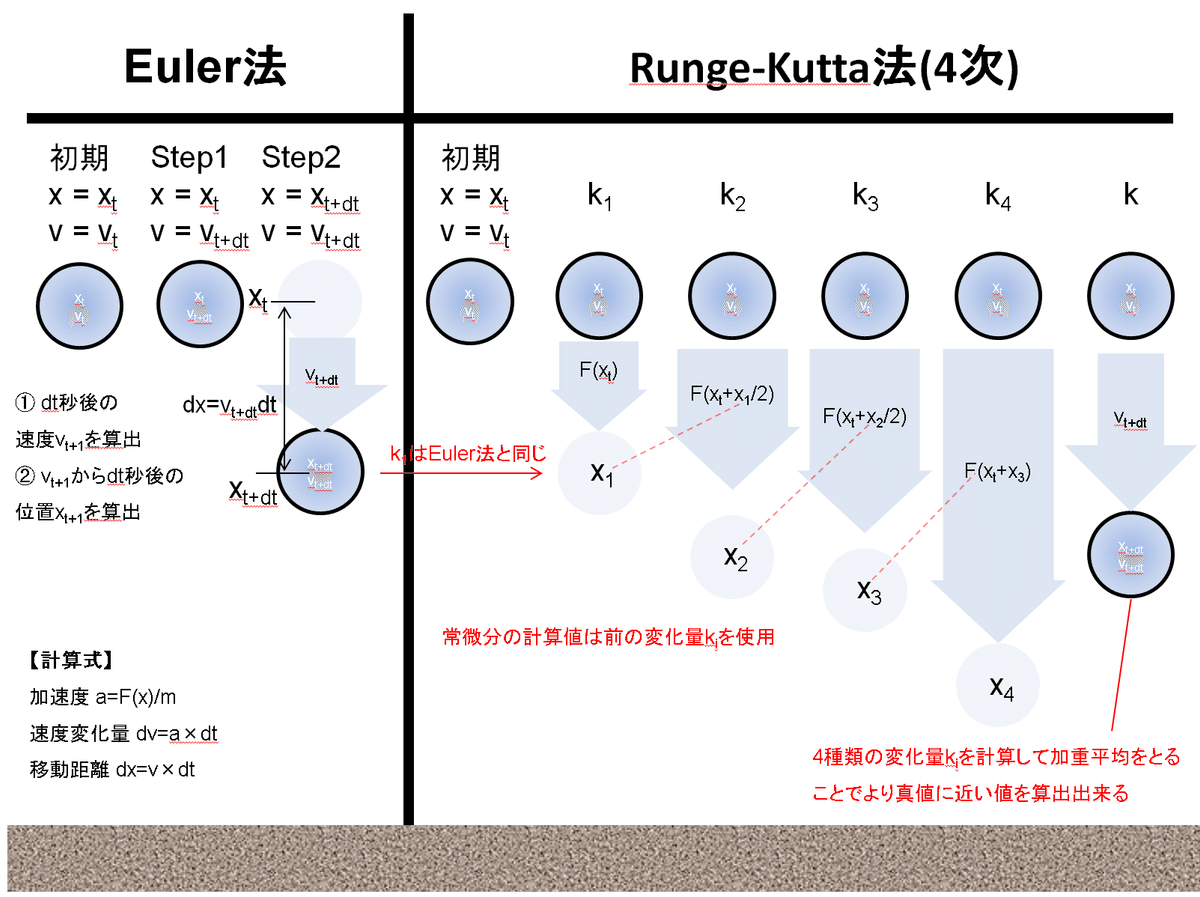
Euler法やLeap-Frog法より、より高精度・高次元の数式に対応する場合はRunge-Kutta法を使用します。
Runge-Kutta法には何種類か計算方法がありますが一般的な4次の解法を使用します。細かい部分は別記事に記載しました。
$$
RungeKutta:y_{n+1}=y_{n}+\frac{k_{1}+2k_{2}+2k_{3}+k_{4}}{6}
$$
$$
dxにおける変化量dy:\frac{k_{1}+2k_{2}+2k_{3}+k_{4}}{6}
$$
4-1.数式の理解
Runge-Kuttaの公式理解は別記事にまとめているため今回は万有引力で使用する場合の公式を記載します。
4-1-1.一般的なRunge-Kutta法に合わせた記法
【速度変化(万有引力の場合)】
$$
dt後の速度変化:v_{t+dt}=v_{t}+\frac{k_{v1}+2k_{v2}+2k_{v3}+k_{v4}}{6}dt
$$
$$
k_{v1}(tでの加速度1)=\frac{f(x_{t})}{m}
$$
$$
k_{v2}(t+\frac{dt}{2}での加速度2)=\frac{f(x_{t}+\frac{k_{x1}}{2})}{m}
$$
$$
k_{v3}(t+\frac{dt}{2}での加速度3)=\frac{f(x_{t}+\frac{k_{x2}}{2})}{m}
$$
$$
k_{v4}(t+dtでの加速度4)=\frac{f(x_{t}+k_{x3})}{m}
$$
【位置変化(万有引力の場合)】
$$
dt後の移動距離:x_{t+dt}=x_{t}+\frac{k_{x1}+2k_{x2}+2k_{x3}+k_{x4}}{6}dt
$$
$$
k_{x1}(tでの速度1)=v_{t}
$$
$$
k_{x2}(t+\frac{dt}{2}での速度2)=v_{t}+\frac{k_{v1}dt}{2}=v_{t}+\frac{\frac{f(x_{t})}{m}dt}{2}
$$
$$
k_{x3}(t+\frac{dt}{2}での速度3)=v_{t}+\frac{k_{v2}dt}{2}=v_{t}+\frac{\frac{f(x_{t}+\frac{k_{x1}}{2})}{m}dt}{2}
$$
$$
k_{x4}(t+dtでの速度4)=v_{t}+k_{v3}dt=v_{t}+\frac{f(x_{t}+k_{x3})}{m}dt
$$
4-1-2.参考:単位統一Ver.
Runge-Kutta法の変化量dtを微分に入れて単位を合わせると下記の通り。
【速度変化(万有引力の場合)】
$$
dt後の速度変化:v_{t+dt}=v_{t}+\frac{k_{v1}+2k_{v2}+2k_{v3}+k_{v4}}{6}
$$
$$
k_{v1}(tでの速度1)=\frac{f(x_{t})}{m}dt
$$
$$
k_{v2}(t+\frac{dt}{2}での速度2)=\frac{f(x_{t}+\frac{k_{x1}}{2})}{m}dt
$$
$$
k_{v3}(t+\frac{dt}{2}での速度3)=\frac{f(x_{t}+\frac{k_{x2}}{2})}{m}dt
$$
$$
k_{v4}(t+dtでの速度4)=\frac{f(x_{t}+k_{x3})}{m}dt
$$
【位置変化(万有引力の場合)】
$$
dt後の移動距離:x_{t+dt}=x_{t}+\frac{k_{x1}+2k_{x2}+2k_{x3}+k_{x4}}{6}
$$
$$
k_{x1}(速度k_{v1}での移動距離)=v_{t}dt
$$
$$
k_{x2}(速度k_{v2}での移動距離)=(v_{t}+\frac{k_{v1}}{2})dt=(v_{t}+\frac{\frac{f(x_{t})}{m}dt}{2})dt
$$
$$
k_{x3}(速度k_{v3}での移動距離)=(v_{t}+\frac{k_{v2}}{2})dt=(v_{t}+\frac{\frac{f(x_{t}+\frac{k_{x1}}{2})}{m}dt}{2})dt
$$
$$
k_{x4}(速度k_{v4}での移動距離)=(v_{t}+k_{v3})dt=(v_{t}+\frac{f(x_{t}+\frac{k_{x2}}{2})}{m}dt)dt
$$
4-2.Pythonコード(関数化)
4-2-1.メイン関数
Runge-Kutta法をコード化するためクラス化して機能は下記の通りです。
初期化(インスタンス作成時)に①微小時間dtと②位置heightから万有引力を計算できる関数 を渡す。
Runge-Kutta法ではv1->x1->v2->x2・・のように連続して計算が必要である。よって速度と位置を計算する関数は一つにして最終的な出力は速度変化dvと位置変化dxを出力するようにした。
Runge-Kuttaの変化量が確認できるようにlogging_data()メソッドを作成してクラス内のリストに保存できるようにした
[IN]
#Runge Kutta法
class RungeKutta:
def __init__(self, dt, func_force, log_verbose=True):
self.dt = dt
self.func_force = func_force #万有引力計算用関数
self.log_verbose = log_verbose #ログ出力の有無
self.output_v = {'k1':[], 'k2':[], 'k3':[], 'k4':[], 'k':[]}
self.output_x = {'k1':[], 'k2':[], 'k3':[], 'k4':[], 'k':[]}
def step_velheight(self, v_init, h_init, mass):
force_init = self.func_force(mass, h_init) #初期値:heightでの万有引力
#k1
diff_v1 = (force_init/mass)*self.dt #dv = (F/m)*dt
diff_x1 = v_init*self.dt #dx = v*dt
#k2
diff_v2 = (self.func_force(mass, h_init+diff_x1/2)/mass)*self.dt
diff_x2 = (v_init+diff_v1/2)*self.dt
#k3
diff_v3 = (self.func_force(mass, h_init+diff_x2/2)/mass)*self.dt
diff_x3 = (v_init+diff_v2/2)*self.dt
#k4
diff_v4 = (self.func_force(mass, h_init+diff_x3)/mass)*self.dt
diff_x4 = (v_init+diff_v3)*self.dt
#k:Runge-Kutta法による加重平均
diff_v = (diff_v1+2*diff_v2+2*diff_v3+diff_v4)/6
diff_x = (diff_x1+2*diff_x2+2*diff_x3+diff_x4)/6
#結果の格納
if self.log_verbose:
self.logging_data(self.output_v, {'k1':diff_v1, 'k2':diff_v2, 'k3':diff_v3, 'k4':diff_v4, 'k':diff_v})
self.logging_data(self.output_x, {'k1':diff_x1, 'k2':diff_x2, 'k3':diff_x3, 'k4':diff_x4, 'k':diff_x})
return diff_v, diff_x
def logging_data(self, datas, params):
for key, value in params.items():
datas[key].append(value)
[OUT]4-2-2.シミュレーション
シミュレーションは下記を繰り返し計算するだけです。計算の収束条件は自分で決める必要があるため移動距離が100m(地面に到着)したら終了する用にループを決めました。
現在の位置(高さ)から重力(万有引力)forceを計算(加速度の算出用)
微小時間dt後の速度変化dv、移動変化dhをRunge-Kutta法(step_velheight()メソッド)で算出
変化量からdt秒後の速度v=v+dt、高さh=h+dhを算出
[IN]
#計算条件
g = 9.80665 #重力加速度
mass = 1.0 #質量
height = 100 #高さ
dt=0.01 #時間刻み[sec]
force = mass*g #重力
#初期条件
time = 0.0 #動作時間[s]
v0=0.0 #速度の初期値[m/s]
#Data格納用
datas.reset() #データの初期化
print(datas.output())
datas(time, height, v0) #初期値を格納
#Leap-Frog法
rungekutta = RungeKutta(dt, universal_grav)
count = 0
v = v0 #初速度
while 0<=height:
force = universal_grav(mass, height) #現在の位置での万有引力
diff_v, diff_x = rungekutta.step_velheight(v, height, mass)
v_next = v + diff_v
height_next = height - diff_x #変化量dx
v, height = v_next, height_next #v, heightを更新
time += dt #時間を更新
#データ追加:100msごと+最後の1回
if count%10==0 or height<=0:
datas(time, height, v) #データを格納
count += 1
output = datas.output()
print(f'落下地点での結果 t={output["time"][-1]:.3f}s, h={output["height"][-1]:.2f}[m], v={output["velocity"][-1]:.3f}[m/s]')
[OUT]
落下地点での結果 t=4.520s, h=-0.17[m], v=44.325[m/s] こちらの結果は今回はLeap-Frog法と同じ時間・速度になりました。理由として地球の半径が$${10^6}$$オーダーのため高さheightの影響は0.01%程度の影響しかないためです。
参考用にアニメーションも作成しました。
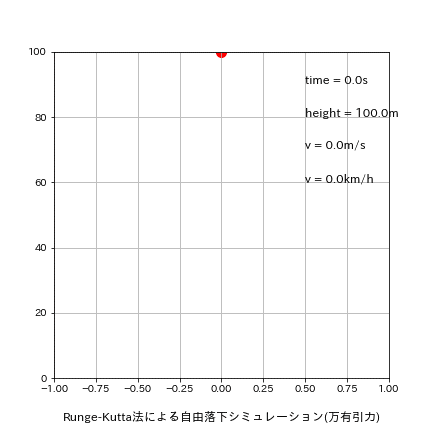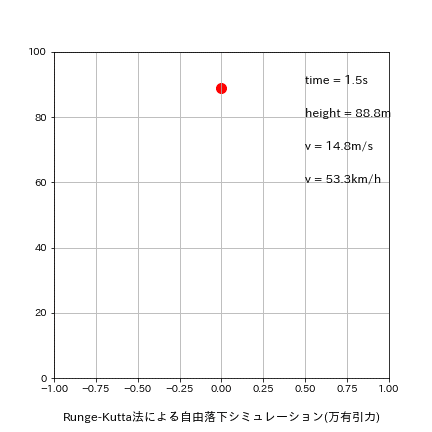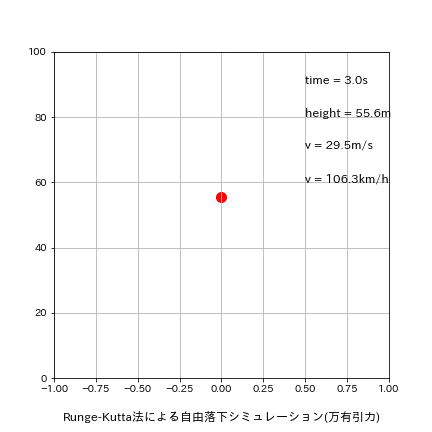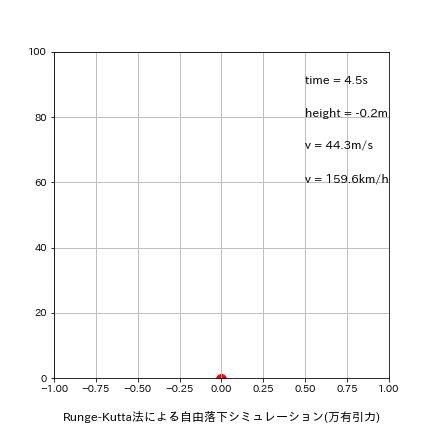
また速度変化と位置変化もログから確認できます。速度変化(つまり加速度)は地表に近い(時間が経つ)ほど値は大きいですが影響はほとんどありません。距離変化(つまり速度)は地面に近づくほど大きくなっております。
[IN]
class HorizontalDisplay:
def __init__(self, *args):
self.args = args
def _repr_html_(self):
template = '<div style="float: left; padding: 10px;">{0}</div>'
return "\n".join(template.format(arg._repr_html_())
for arg in self.args)
df_v = pd.DataFrame(rungekutta.output_v)
df_x = pd.DataFrame(rungekutta.output_x)
display(HorizontalDisplay(df_v, df_x))
[OUT]
5.補足資料
5-1.刻み幅hの影響確認
刻み幅dt(またはh)を変化させて精度がどのようになるか比較しました。結論としては「初期条件を正しく設定しないと計算精度の高いアルゴリズムを使用しても良い結果は出ない」です。
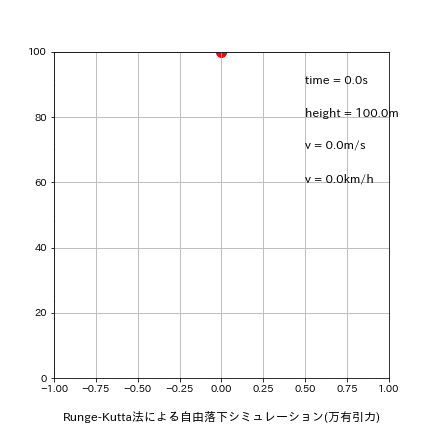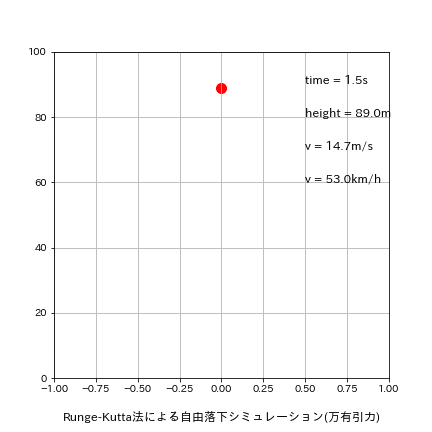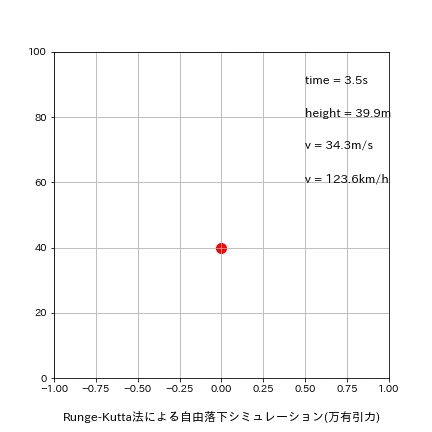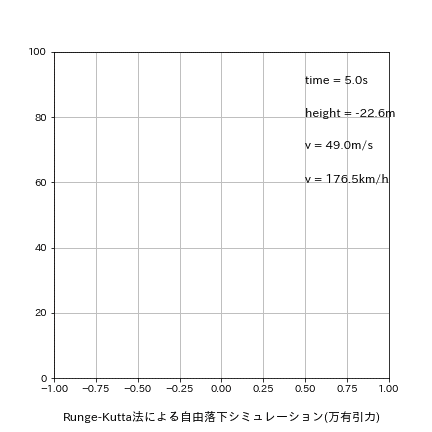
5-1-1.刻み幅dt=0.5
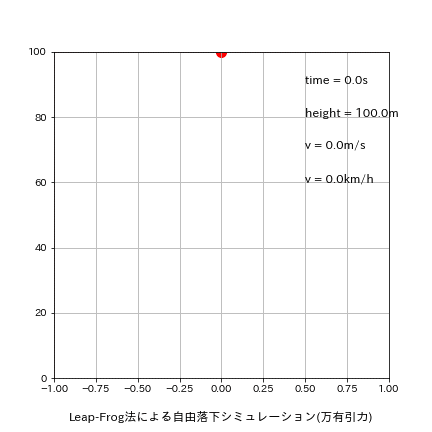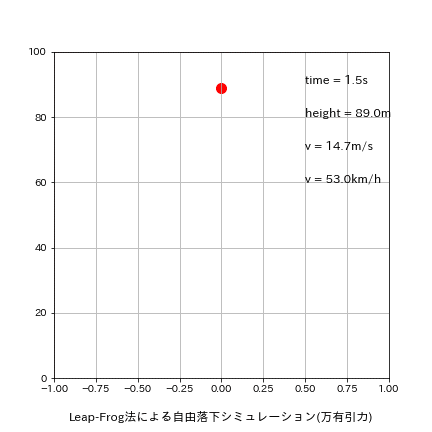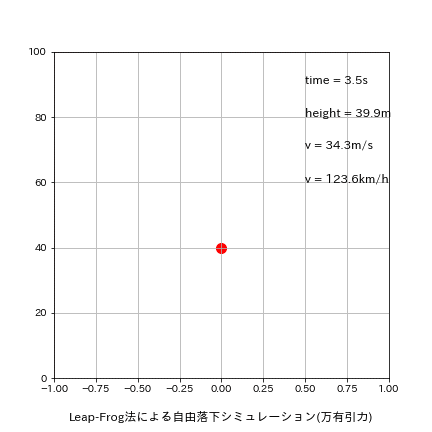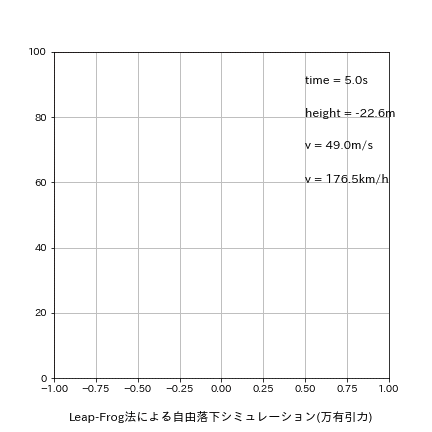
刻み幅dxを0.01s->0.5sに変更して再計算した結果は下記の通りです。
理論値time:4.516s、v:44.287m/sに関して今回はたまたまEuler法の方が良い結果が出ました。
[output]
Euler:落下地点での結果 t=4.500s, h=-10.32[m], v=44.129[m/s]
Leap-Frog:落下地点での結果 t=5.000s, h=-22.58[m], v=49.032[m/s]
Runge-Kutta:落下地点での結果 t=5.000s, h=-22.58[m], v=49.032[m/s]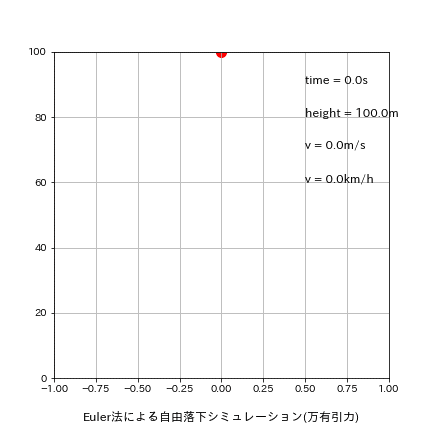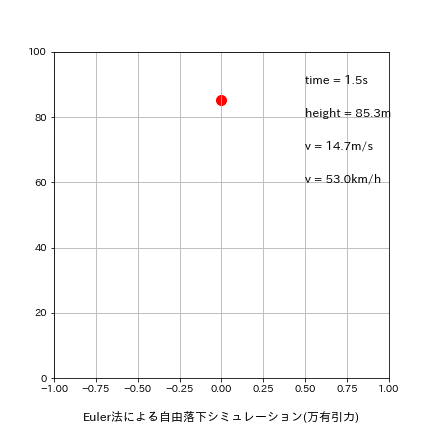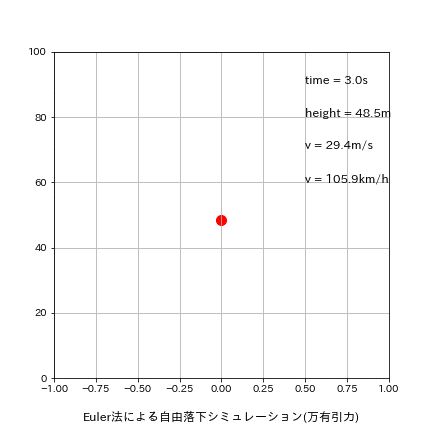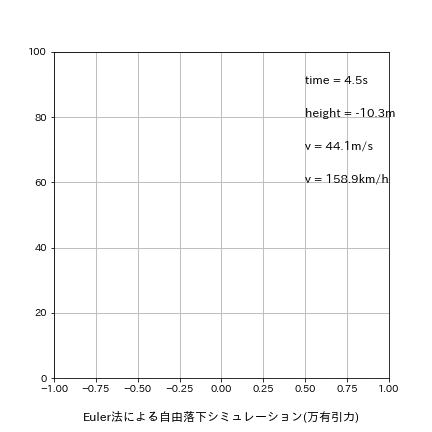
5-1-2.刻み幅dt=1.0
刻み幅dxを0.01s->1.0sに変更して再計算した結果は下記の通りです。
理論値time:4.516s、v:44.287m/sに関して今回はほぼ同じ結果となりました。先ほどの結果と合わせるとRunge-Kutta法は補正能力が高い(刻み幅に対してロバスト)ことが分かります。
[output]
Euler:落下地点での結果 t=5.000s, h=-47.10[m], v=49.032[m/s]
Leap-Frog:落下地点での結果 t=5.000s, h=-22.58[m], v=49.032[m/s]
Runge-Kutta:落下地点での結果 t=5.000s, h=-22.58[m], v=49.032[m/s]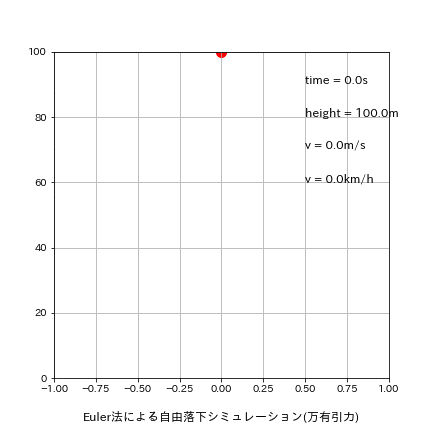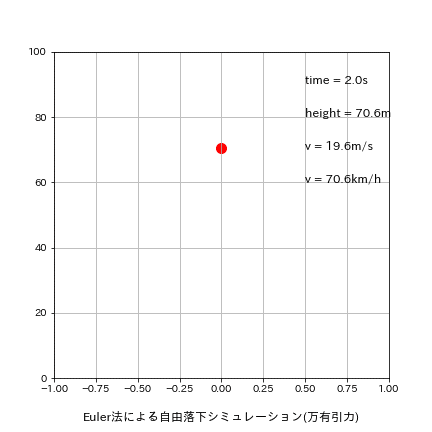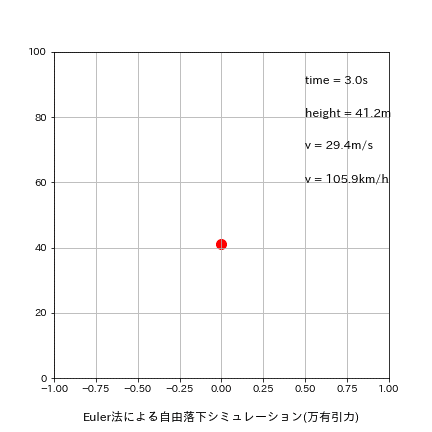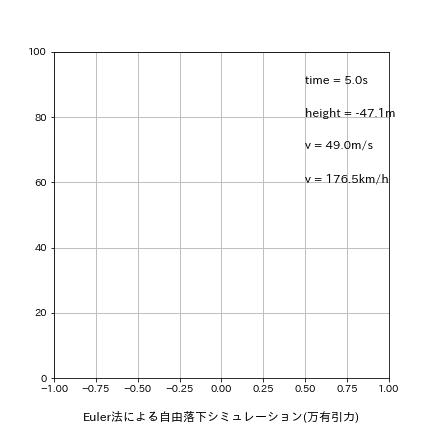
5-2.常微分方程式の法則一覧
化学工学などで紹介される1次元の常微分方程式を紹介します。法則は基本的に「移動量=係数×勾配」であり同じ形となります(熱・濃度・速度の勾配がある方向に量が移動する)。
https://ocw.nagoya-u.jp/files/174/00TRTEXT.pdf
【フーリエの法則:1次元の熱移動】
伝熱速度q [J/s]、固体の熱伝導度k [J/(m・s・K)]、伝熱面積A [m2]、温度勾配dTdx [K/m]
$$
q=-kA \frac{dT}{dx}
$$
【フィックの第一法則:1次元の物質拡散】
J:拡散流速、D:拡散係数、c:濃度 ,Cc :カニンガムの補正係数, k:ボルツマン定数, T:温度, μ:粘度
$$
J = -D \frac{dC}{dx}
$$
$$
D = C_{\mathrm{c}}\frac{kT}{3 \pi \mu D_{\mathrm{p}}}
$$
【ニュートンの粘性法則:1次元の剪断応力】
τ摩擦応力 [Pa]、μ粘性係数 [Pa・s]、u流体の速度 [m/s]、y流体ー流体間または流体ー物体間の距離 [m]
$$
\tau=\displaystyle \mu \frac{du}{dy}
$$

参考記事
あとがき
それにしても大学院の時にパラメータを求める手法に「Runge-Kutta法がある」って話を聞いてたけど教えてもらえずだったが、今になって再勉強するとは思わなかった・・・・・
この記事が気に入ったらサポートをしてみませんか?
