【第31回】母平均の区間推定-後編
前回に引き続き、情報Iの授業で区間推定の考え方を扱う方法について考えていきたいと思います。
前回記事では、いろいろと端折ってとにかく95%信頼区間を求めるための最低限の流れになってしまいました。
数学Bで学ぶ数学的な内容を避けてできるだけ直観的に理解できるよう努めた結果、かえって説明が分かりにくくなっていたところが反省点です。
そこで、今回は連続型確率変数について、大まかな説明をし、これを積極的に使って区間推定を考えてみたいと思います。
確率変数と確率分布
まずは直観的に捉えやすい二項分布を利用して確率変数や確率分布の説明を行うことにします。
離散型確率変数
サイコロを100回投げたときに1の目が出る回数を$${ X }$$とするとき、1の目がちょうど$${ k }$$回出る確率、つまり、$${ X=k }$$となる確率(これを$${ P(X=k) }$$と書きます)は次の式で与えられます。
$$
P(X=k) = _{100}C_k\left( \frac{1}{6} \right)^k \left( \frac{5}{6} \right)^{100-k}
\quad (k=0,1,2, \cdots , 100)
$$
この$${ X }$$のような、起こり得ることに対して値が決まる変数を確率変数といい、確率変数の値とそれに対応する確率の対応関係を確率分布といいます。
$${ X }$$は1, 2, 3, … のようなとびとびの値をとり、このような値を離散値ということから、$${ X }$$を離散型確率変数といい、離散型確率変数と確率の対応関係を離散型確率分布と言います
この場合において1の目が出る回数が10回以上20回未満である確率$${ P( 10 \leqq X < 20) }$$は、
$${ P( 10 \leqq X < 20) =P( X=10) + P(X=11) + \cdots + P(X=19) }$$
であり、前回記事で見ましたように下のヒストグラムの10本の柱の面積の合計になることに注意をしてください。

なおここで考えたのは、一定の確率$${ p }$$で起こる2つの事象のうち一方が起こる試行を$${ n }$$回行ったときにできる確率分布で、二項分布といいます。
連続型確率分布
一方で、前回の記事で考えました身長のデータです。
身体測定のときは、小数第1位までの値として丸めるのが普通で、現実的には離散値ですが、理論上は実数値をとります。
従いまして、取りうる値が無数にあるわけです。
150.0と150.1の間に、150.00と150.01があり、さらにその間に150.000と150.001があるというように、2つの実数間には無数の実数がぎっしりとつまっています。このような値を連続値といいます。
したがって、特定の値をとる確率というのがもはや考えることはできません。ではどのように考えるかですが、人間は無限を目で見るのはできないことから、限りなく大きい数で代用します。
例えば、100万人の身長を考え、さらに階級幅を0.01にして考えてみます。
このときの、ヒストグラムは次のようになり、100万人の中から無作為に1人を選んだときに、その人の身長が「165cm以上175cm未満」である確率$${ P( 165 \leqq X < 175) }$$は、下のヒストグラムの1000本の柱の面積の合計になります。

これは、上の図のオレンジ色の曲線と横軸の間の$${ 165 \leqq X < 175) }$$の部分とほぼ等しいと言えます。
この$${ X }$$のような、連続値をとる確率変数を連続型確率変数といい、離散型確率変数と確率の対応関係を離散型確率分布と言います。
連続型確率変数がある範囲の値をとる確率が、上のオレンジ色の曲線と横軸間の面積で表されているとき、この曲線をグラフに持つような関数を確率密度関数と言います。
正規分布
正規分布は自然現象や社会現象でみられる連続型確率分布で、その確率密度関数のグラフは平均値をピークとした左右対称の山型になることが知られています。

ここでは、正規分布の確率密度関数は平均と分散によって定まっているということをおさえて先に進みましょう。
標本平均の確率変数
母集団から大きさ$${ n }$$の標本を取り出したとき、その標本平均$${ \overline{X} }$$もまた確率変数です。
以下、前回記事でも確認しましたが、次の事実を使います。
母集団の平均が$${ m }$$、標準偏差が$${ \sigma }$$であるとき、標本平均$${ \overline{X} }$$は、標本の大きさ$${ n }$$が十分に大きいときには平均が$${ m }$$、標準偏差が$${ \frac{\sigma}{\sqrt{n}} }$$の正規分布に近づく。
区間推定の数学的説明
前回、95%信頼区間をPythonのプログラムを利用して求めましたが、その意味を今回は考えてみましょう。
母集団の平均が$${ m }$$で未知、標準偏差が$${ \sigma }$$で既知あるとします。母平均が分からないのに母分散が分かっているのは何とも不自然な状況ですがここでは一度、このような仮定で考えます。
このとき、母集団から無作為に抽出した大きさ$${ n }$$の標本について、$${ n }$$が十分に大きいとき、標本平均$${ \overline{X} }$$は平均が$${ m }$$、標準偏差が$${ \frac{\sigma}{\sqrt{n}} }$$の正規分布に従うとみなせます。
このとき、次のような確率変数$${ Z }$$を考えます。
$$
Z = \frac{ \overline{X} - m }{\frac{\sigma}{\sqrt{n}}}
$$
これは、標本平均$${ \overline{X} }$$と母平均の差が標準偏差の何倍ずれているかを表した変数であり、$${ Z }$$は平均0、分散1の正規分布に従います。
前回の記事の95%信頼区間は、$${ P(|Z| \leqq k ) =0.95 }$$となる$${ k }$$の値をもとに算出されています。この$${ k }$$の値を求めてみましょう。
Pythonでは$${ P(X \leqq x_0 ) =\alpha }$$を満たす$${ x_0 }$$の値を求めるようなメソッドが用意されており、この場合は下の図より、$${ \alpha = 0.025, 0.975 }$$となるような$${ x_0 }$$の値の値を求めればよいわけです。

from scipy import stats
stats.norm.ppf(0.025), stats.norm.ppf(0.975)実行結果:(-1.9599639845400545, 1.959963984540054)
およそ$${ \pm1.96 }$$です。したがって、次のようなことが言えます。
$$
P \left( -1.96 \leqq \frac{ \overline{X} - m }{\frac{\sigma}{\sqrt{n}}} \leqq 1.96 \right) = 0.95
$$
上の式の( )内を変形すると、
$$
m - 1.96 \cdot \frac{\sigma}{\sqrt{n}} \leqq \overline{X} \leqq m + 1.96 \cdot \frac{\sigma}{\sqrt{n}}
$$
となります。大きさ$${ n }$$の標本を抽出して、実際に標本平均を求めたときの値$${ \overline{x} }$$が、$${ m \pm1.96 \cdot\frac{\sigma}{\sqrt{n}} }$$である範囲である確率が95%という意味です。
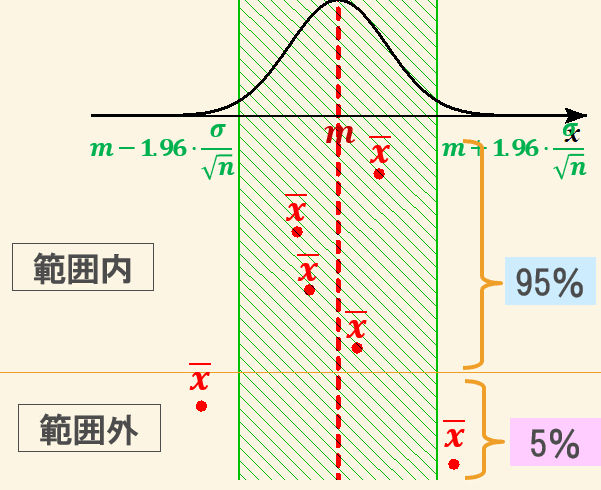
この実測値$${ \overline{x} }$$を代入して、$${ m }$$について解いた不等式
$$
\overline{x} - 1.96 \cdot\frac{\sigma}{\sqrt{n}} \leqq m \leqq \overline{x} + 1.96 \cdot\frac{\sigma}{\sqrt{n}}
$$
が無作為抽出された標本から得られる母平均$${ m }$$の95%信頼区間であったということです。
前回、母平均MEANが未知、母分散$${ 5.76^2 }$$である母集団から大きさ100の標本を無作為抽出したところ、その標本平均が170.5634581618334であったという例を考えました。
この例において、次のプログラムを実行して95%信頼区間を求めました。
samp = stats.norm.rvs(loc=MEAN, scale=5.76, size=100) # MEANは乱数で発生
stats.norm.interval(0.95,loc=samp.mean(),scale = 5.76/10)実行結果:(169.43451890673833, 171.6923974169285)
これは次の不等式の下限値と上限値を計算していたことに他なりません。
(標本平均を小数第2位までの値に丸めます。)
$$
170.56 - 1.96 \cdot\frac{5.76}{\sqrt{100}} \leqq m \leqq 170.56 + 1.96 \cdot\frac{5.76}{\sqrt{100}}
$$
以上が、前回実行したプログラムの意味でした。

まとめ
2回に渡って区間推定についてまとめてみましたが、正直な感想としましては、思っていたよりも説明が難しいということです。
95%信頼区間を求める不等式に当てはめて信頼区間を求めたり、それをPythonを使って簡単に計算させることができたとしても、信頼区間の意味を理解するの別物です。
母平均の推定は考え方がそれほど難しくないのですが、直観的に捉えるレベルとはいえ誤解を避けようと議論をすると確率変数や確率分布の話はどうしても避けて通れません。
当初、推定の方が検定よりも考え方が自然で伝わりやすいのではという問題提起をして書き始めたでしたが、自分の中ではそれほど変わらない、あるいは推定の方が難しく感じるのではないかと考え直したところです。
生徒の習熟度や数学の授業の進度に合わせながら、情報Iではどのようなテーマを取り上げて考えてみるのかを考えていくのが今後の課題になります。
今後、もう少し自分の中で考え方がまとまってきましたら改めて記事を書いてみたいと思っています。
というわけで、今回はやや中途半端な終わり方になってしまいました。
ちょっと見切り発車で記事を書いてしまった感がありましたが、実際に記事にしようと思ったから分かったことも多かったので収穫が多かったです。
最後までお読みいただきありがとうございました。
