【第30回】母平均の区間推定-前編
本シリーズの記事も30回目になりました。
いつもお読みいただいているみなさま、本当にありがとうございます。
今回から、情報Iの授業で区間推定の考え方を扱う方法について考えていきたいと思います。
情報Iの授業の中で、コンピュータを活用しながら区間推定の考え方を学ぶことで、標本のデータから母集団の性質を確率に基づいて推測する方法に慣れることを目指してみたいと思っています。
本記事の内容
本記事では、授業1回完結を目指し、次のような流れで書いていこうと思っています。
正規分布とその例
標本平均の分布
区間推定の考え方 ←本記事(前編)はここまで
区間推定の数理的な説明 →次記事(後編)で
「データの分析」(数学I)の分散と標準偏差、「場合の数と確率」(数学A)の確率の基本性質はすでに学習済みであることを想定します。
一方で、数学Bの「統計的な推測」は未習であると想定し、確率変数や確率分布についてはまだ本格的に学習していないとします。ここが正直、難しいところであり、どれだけ直観的に捉えながら説明できるかの勝負どころになります。
前置きが長くなってしまいましたが、さっそく見ていきましょう!
正規分布とその例
今回は、高校1年生男子の身長の例を使って考えていきたいと思います。
e-Statの「令和2年度 学校保健統計調査」のデータを利用しました。
「身長の年齢別分布」(表番号2)では身長が次のように、1cm刻みの階級とその相対度数がまとめられています。
簡単のために身長の列の「150cm」は「150cm以上151cm未満」を表しているものと解釈します。
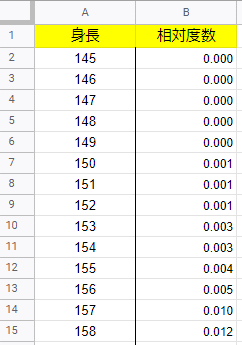
これをもとにPythonでヒストグラムと折れ線グラフを描いてみたいと思います。

また、上のサイトで「年齢別 都市階級別 設置者別 身長・体重の平均値及び標準偏差」(表番号1)を参照しますと、令和2年度調査における16歳男子の身長の平均値は170.0、標準偏差は5.76であることが分かります。
ここで、上の相対度数の分布を表した折れ線グラフは、平均値の170cmをピークにした左右対称の釣鐘状に近い形をしています(下の赤色のグラフ)。
このようなグラフで表されるような分布を正規分布と言います。

16歳男子のうち、身長が165cm以上175cm未満の人は全体のどれくらいの割合かを考えてみます。
これは、165cm~174cmまでの10個の階級の相対度数の和になり、0.602になることが分かります。
ヒストグラムの各柱の横の長さは1で、縦の長さがその階級での相対度数であることに注意しますと、これは10本の柱の面積の和と言い換えられます。

さらにこれは、正規分布を表すグラフにおいて、165以上175未満の幅におけるグラフの下の面積に相当します。この面積を求めると、0.6146でおおよそ上で求めたものに近い値になります。
標本平均の分布
それでは、母集団の分布が平均170、標準偏差5.76であるときに、そこから無作為に100個の値を取り出した標本を考えてみましょう。
scipy.statsモジュールのnorm.rvsメソッドを利用すると、指定した平均、標準偏差の正規分布に従うような乱数を複数個発生させることができます。
from scipy import stats
samp = stats.norm.rvs(loc=170.0, scale=5.76, size=100)
samp実行結果:

この標本における100個の値の平均を求めるには次のようにします。
samp.mean()実行結果(例):170.29829905607673
母集団の平均が170.0であることからこれに近い値になりますが、やはり標本である以上はどうしても偏りが出て、誤差が生じます。
そこで大きさ100の標本を抽出し、その標本平均を調べる操作を繰り返し、標本平均の分布を調べてみることにします。
次のようなヒストグラムになりました。

標本平均の分布もまた、正規分布になることが言えそうです。
実際に、中心極限定理という統計学の基本的な定理により、次のことが知られています。
母集団の平均が$${ m }$$、標準偏差が$${ \sigma }$$であるとき、大きさ$${ n }$$の標本の平均の分布は、$${ n }$$が十分に大きいときには平均が$${ m }$$、標準偏差が$${ \frac{\sigma}{\sqrt{n}} }$$の正規分布に近づく。
今回はこの事実を使って、考えていきたいと思います。
区間推定の考え方
取り出した標本の標本平均だけで母平均を推測するのは、標本による誤差の影響を大きく受けます。
そこで、取り出した標本の標本平均と母集団の分散の値から、母平均が高い確率で含まれている区間を求めることで、ある程度の幅を持たせて母平均の値を推測することを考えてみます。
これが区間推定の基本的な考え方で、高い確率で母平均が含まれる区間のことを信頼区間と言います。
また、この高い確率としては95%や99%が使われることが多く、それぞれ95%信頼区間、99%信頼区間と呼ばれています。
理論的なことは次回まとめることにしまして、まずはPythonを利用して95%信頼区間を求める方法を今回は整理します。
そのための下準備として、未知の母平均MEANを167から173の間の乱数を発生させて決めてみたいと思います。このMEANを後で推定します。
import numpy as np
r = np.random.random()
MEAN = (1-r) * 167 + r * 173このMEANを出力せずに伏せたままにしておくことで、これを未知の母平均と見立てることにします。
母集団の分布が、母平均が上で求めたMEANの値、母標準偏差が5.76(16歳の男子と同じ)の正規分布であるとします。
そこから、大きさ100の無作為標本を抽出します。次のコードです。
samp = stats.norm.rvs(loc=MEAN, scale=5.76, size=100)
samp実行結果(例):

標本平均を求めてみます。
samp.mean()実行結果(例):170.5634581618334
標本平均が上の値であることから、母平均も大体この値前後なのかと推定できます。
最後に次のメソッドを使って信頼区間を求めます。
stats.norm.interval(信頼度, loc = 標本平均, scale = 母標準偏差 $${ / \sqrt{n} }$$)
stats.norm.interval(0.95,loc=samp.mean(),scale = 5.76/10)実行結果:(169.94386955385374, 172.2017480640439)
これが95%信頼区間です。
これは母集団から標本をとって、標本平均を調べ、信頼区間を求めてという作業を行ったときに、それが母平均を含む区間であるような頻度が95%(100回のうち95回の割合)であるということを意味しています。
最後に、本来は分からない母平均ですが今回は最初に、乱数で母平均MEANを決めていました。この値を出力してみましょう。
MEAN実行結果:170.9100313191108
今回は、母平均を含む区間が得られるような標本だったようです。
いったんまとめ
今回は、いろいろと端折ってとにかく95%信頼区間を求めるための最低限の流れになってしまいました。
また、確率変数を使って式変形をするとすっきり説明できたものが、それを避けて直観的に捉えようとすればするほど、かえって説明が冗長になって分かりにくくなってしまったところが反省点です。
次回は確率変数を使って理屈付けをしつつ、区間推定のポイントをまとめて参りたいと思っています。
「直観的に考え方を学ぶ」という観点では仮説検定の方がむしろ分かりやすかったのかもとちょっとずつ思い直しました。
迷走しないように、次回の記事を書いた後にこのあたりをもう一度、しっかりと検証してみます。
最後までお読みいただきありがとうございました。
