固有値にまつわる思い出話

2024年3月7日 12:52

はじめに

株式会社GA technologiesの福中です。AI Strategy Center（以下AISC）という部署でChief Data Scientistとして働いています（詳しい自己紹介はAISC WEBサイトのプロフィールをご覧ください）。今、Data Scienceチームでは数学勉強会を週1で実施していて、メンバーのみんなで線形代数学と初等解析を勉強しています。

線形代数と解析は、統計学や機械学習を理解するうえで非常に重要な概念で、データサイエンスを専門とする人なら誰しもが1度は勉強すると思います。ただ、重要な反面、その抽象度の高さに（特に人文科学系の人ほど）苦手意識を持つ人も少なくありません。それゆえ、1人で勉強するとついつい後回しになってしまい、途中で挫折する人が多かったりする分野でもあります。そこで「勉強会」という形である程度の強制力を持たせ、「逃げずに最後まで勉強する！」というのがこの勉強会を企画した趣旨になります。このあたりのことは、詳しくは以下、AISCメンバーの白圡さんの記事をご覧ください。

今回この白圡さんの記事に続き、数学勉強会を通じて考えたこと、感じたことを、「何でも良いので記事にしよう！」ということでブログを書くことになりました。「何でも良い」と言われると難しいのですが、僕は学生時代に学んできたことを思い出しつつ、固有値にまつわる思い出話を記事にしようと思います。

心理学の衝撃

さて、少し学生時代の話をしましょう。僕はもともと教育学部の心理臨床を専攻しており、高校生の時は、将来は心理カウンセラーになりたくて大学に進学しました。しかし、授業を受けていく中で分かったのですが、僕が思っていた心理学と大学で学問として学ぶ心理学には大きな乖離がありました。

将来心理カウンセラーになりたいと思っていたことからも分かるように、僕の思っていた心理学とは主にカウンセリングが中心だったのです。人の悩みを聞き、カウンセリングを経てその人の問題を解決すること。それこそが心理学だと考えていました。

しかし、大学ではカウンセリングは心理学の一部でしかなく、学問としての基礎は実験心理学にあると教えられます。その歴史は意外に新しく、1879年にドイツの生理学者Wilhelm Maximilian Wundtがライプツィヒ大学に心理学実験室を開設したことが自然科学としての心理学の始まりだと言われています。僕が大学生になったのは2000年だったので、せいぜい120年程度の歴史しかないことに大変驚いた覚えがあります。

心理統計学の衝撃

心理学では「心」という目に見えない概念を扱います。そのため、その「目に見えない心」をどのように測定すべきか、定量化の手段が重要になってきます。そして、科学的であるために、データを収集して分析する工程が必ず発生します。そのため、心理学を専攻する学生は、心理統計学の授業が必修科目として準備されており、必ず履修する必要があります。僕も大学3年生の時に受講しました。

ただ、心理学は本来文理融合領域の学問になるのですが、高校生の時にはそのようなことを意識せずに進学する人が多いので、どちらかというと文系の比重が多くなっているようです。実際、僕の同期も85％の人が文系でした。（ただ、現在では状況は変わっているかもしれません）

そして、文系の人はこの心理統計学を苦手にしている人が多いようです。僕の友人の中には「数学が嫌で文系を選択したのになんで大学でも数学みたいなことやらなければいけないんだ！」と言っている人もいたくらいです笑

因子分析の衝撃

学部の3年生で最初に学ぶ心理統計学の授業は、統計的仮説検定から始まり、一般的な多変量解析について一通り学習するという極めて一般的なカリキュラムでした。その授業の最後に登場する手法が因子分析(factor analysis)です。因子分析がどのような手法かについては別の記事で書いたので、そちらをご参照ください。

因子分析1：とりあえず1因子モデルを構築してみる
 因子分析2：探索的因子分析の実践
 因子分析3：尺度構成のための因子分析
 因子分析4：カテゴリカル因子分析
 因子分析5：確認的因子分析

当時の僕にとって、因子分析は大変難しい手法に感じました。因子分析の目的は理解できるし、やろうとしていることや使い方はわかるのですが、どうやってその値が算出されているかがわからず、結果的に「なんだかもやもやする」、そんな印象を持ちました。「調べればよいじゃないか」と思われるかもしれませんが、実際図書館で因子分析の専門書を開くと羅列されている数式に圧倒され、何の参考にもなりませんでした。

当時は因子分析をわかりやすく説明する書籍はまだまだ少なく、
芝祐順 (著)　因子分析法
 柳井晴夫 (著)　因子分析―その理論と方法
などが代表的な参考書として紹介されていました。しかしながら、中身を見てみるとわかるのですが、線形代数も知らないような文系学生が読めるものではなかったのです。

その結果、理論を理解することなく、天下り的に受け入れてサンプルをまねして使うだけになってしまっていました。とても「使いこなしている」とは言えませんね笑

固有値の衝撃

「使うだけ」と言ってもやっぱり腑に落ちないところがありました。その代表例が固有値(eigen value)です。因子分析における固有値は、因子数を決定するために使われる指標で、突然、何の前触れもなく、（初心者用のわかりやすい系の本では）詳しい説明もなく、登場します。例えば、ガットマン基準では「固有値が1以上の因子数のうち最大のものを採用する」というような使われ方をします。使い方はいたって簡単です。

しかし、なぜ1以上を採用するのでしょう？そもそも固有値ってどういう意味を持っていて、なぜ因子数を決定する際の情報として使うのでしょうか？当時の僕には全く意味が分かっていませんでした。数学の本を見ても、「行列$${A}$$に対して、以下の方程式

$$
A\boldsymbol{x} = \lambda \boldsymbol{x}
$$

を満たす零ベクトルでないベクトル$${\boldsymbol{x}}$$とスカラー$${\lambda}$$が存在するとき、$${\boldsymbol{x}}$$を$${A}$$の固有ベクトル、$${\lambda}$$を$${A}$$の固有値と呼ぶ。」のようにしか書いていません。間違いではない（というか正しい定義な）のでしょうが、これでは因子分析とは全くつながらず、全然わからなかったのです。

固有値の意味の衝撃

そこで、この固有値とは統計学、特に因子分析の枠組みでどういう意味を持つのか、徹底的に考えてみようと思いました。そこで、まずは以下のようなデータを想定します。これは相関係数が1となるように乱数を発生させて作成したダミーデータになります。

import matplotlib.pyplot as plt
import numpy as np
import pandas as pd

# 特定の相関係数となるような乱数の発生
# 乱数のシードを固定して再現性を確保
np.random.seed(42)

# 乱数を生成する変数の数
num_samples = 10

# 相関係数が1の相関行列を作成
correlation_matrix = np.array([[1, 1], [1, 1]])

# 多変量正規分布に基づいて乱数生成
random_data = np.random.multivariate_normal(mean=[0, 0], cov=correlation_matrix, 
                                            size=num_samples)

# データフレーム
df = pd.DataFrame(data=random_data, columns=["x","y"])

print(df)

          x         y
0 -0.496714 -0.496714
1 -0.647689 -0.647689
2  0.234153  0.234153
3 -1.579213 -1.579213
4  0.469474  0.469474
5  0.463418  0.463418
6 -0.241962 -0.241962
7  1.724918  1.724918
8  1.012831  1.012831
9  0.908024  0.908024

これを散布図としてプロットしたのが以下となります。

ax = df.plot(
    x=df.columns[0],
    y=df.columns[1],
    kind='scatter',
    grid=True,
    xlabel='x',
    ylabel='y')

ax.set_ylim([-2,2])
ax.set_xlim([-2,2])
ax.set_aspect("equal", adjustable="box")

plt.show()

このとき、$${x}$$と$${y}$$の標準偏差を求めると以下のようになります。

# 標準偏差を求める
df.describe().loc['std']

x    0.954121
y    0.954121
Name: std, dtype: float64

また相関係数は以下のようになります。

# 相関係数を求める
cor = np.corrcoef(df['x'].values, df['y'].values)
print(cor)

[[1. 1.]
 [1. 1.]]

当然ですが、相関1ですね。そして、この相関行列を$${A}$$として、$${A}$$の固有方程式を解いて、固有値と固有ベクトルを求めてみましょう。手計算でも求められるのですが、面倒なので今回は以下のようにPythonで計算します。

import numpy.linalg as LA

# 相関行列の固有値と固有ベクトルを計算する
l, p = LA.eig(cor)
print("固有値")
print(l)
print("固有ベクトル")
print(p)

固有値
[2.22044605e-16 2.00000000e+00]
固有ベクトル
[[-0.70710678 -0.70710678]
 [ 0.70710678 -0.70710678]]

するとこのように、固有値が2と0、固有ベクトルが(-0.70710678, -0.70710678)と(0.70710678, -0.70710678)が求められました。次に、この各固有ベクトルを座標点として、それぞれと原点を通る直線を図1に上書きしてみましょう。

ax = df.plot(
    x=df.columns[0],
    y=df.columns[1],
    kind='scatter',
    grid=True,
    xlabel='x',
    ylabel='y')

# 原点を通る傾き1の直線の描画
ax.axline((0, 0), slope=1, color='red', lw=1)

# 原点を通る傾き-1の直線の描画
ax.axline((0, 0), slope=-1, color='blue', lw=1)

ax.set_ylim([-2,2])
ax.set_xlim([-2,2])
ax.set_aspect("equal", adjustable="box")

plt.show()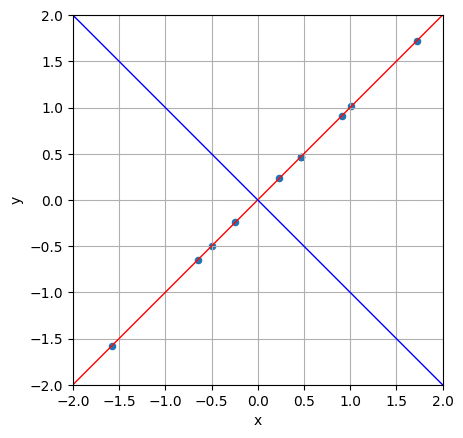

すると、一方の固有ベクトル(-0.70710678, -0.70710678)が10個のダミーデータの上を通り（赤の直線）、その直線と直交する形でもう一方の固有ベクトル(0.70710678, -0.70710678)の直線（青の直線）が描かれていることがわかると思います。

上記では相関係数が1のときの固有値と固有ベクトルを求めましたが、次にいくつかの相関係数のときに固有値と固有ベクトルおよび散布図がどうなるかを見てみましょう。なお、ここからは、特定の相関係数のときの乱数データの発生を5000個としています。

# 相関係数が0.7のとき
固有値
[1.70028343 0.29971657]
固有ベクトル
[[ 0.70710678 -0.70710678]
 [ 0.70710678  0.70710678]]

# 相関係数が0.5のとき
固有値
[1.50041289 0.49958711]
固有ベクトル
[[ 0.70710678 -0.70710678]
 [ 0.70710678  0.70710678]]

# 相関係数が0.3のとき
固有値
[1.3004962 0.6995038]
固有ベクトル
[[ 0.70710678 -0.70710678]
 [ 0.70710678  0.70710678]]

# 相関係数が0のとき
固有値
[1.00728132 0.99271868]
固有ベクトル
[[ 0.70710678  0.70710678]
 [-0.70710678  0.70710678]]

結果を見るとわかるように、（符号の付く位置は変わっていますが）固有ベクトルはすべてもともとの座標軸を45度回転させたものに一致しています。また、相関係数が1のときは固有値の一方が2、もう一方が0でしたが、相関係数が弱くなるに従い、2つの固有値の差が小さくなり、無相関の状況では両方の固有値が約1になっていることがわかります。

つまり、固有ベクトルとは既存の座標軸を回転させた新しい座標軸のことを表しており、その新座標軸でのデータのばらつきの大きさが固有値であることを意味しています。例えば相関係数が1のとき、固有値が0の方の新座標軸はデータのバラツキ（分散）が0になっており、固有値が2の方の新座標軸上でのみデータがばらついています。また、相関係数が0のとき、両方の新座標軸でのバラツキ（分散）は等しく、ゆえに固有値はともに１となります。

以上のことから、例えば相関係数が1の場合、固有値が0の方の新座標軸は、その存在意義が全くありません。なぜならその座標軸ではデータが一切ばらついていないからです。そのため、座標軸は1つで良く、「その座標軸だけでデータは解釈できるよね」ということから次元の削減ができることになります。このあたりの考え方は因子分析だけでなく、主成分分析でも同等ですね。

一方、先ほども述べましたが、相関係数が0のときは、2つの新座標軸において、固有値がともに1でそれぞれの座標軸でのデータのバラツキに差がないことを意味しています。したがって、2つの座標軸の両方が重要で、このデータを解釈するには2つの座標軸をそれぞれ見る必要があるということです。ゆえに次元の削減はできません。ガットマン基準において、固有値を1以上で解釈する必要があるという主張の根拠はここにあります。「固有値1未満の因子はデータを解釈する座標軸として意味ないよね」と判断するということですね。これが固有値の意味であり、統計モデルにおいて固有値がいかに重要な役割を果たしているかがわかると思います。

最後に

いかがでしたでしょうか？数学の概念と現実の事象がつながると、これまで色褪せて見えていた無機質な数式が、途端に輝き始め、興味深く思えないでしょうか？今回の固有値の意味に関しては、僕が最初に統計学に興味を持ち、線形代数をはじめとした数学にはまり始め、統計オタク数学オタクになった原初の体験になります。本ブログを読んで、少しでも統計学や数学に興味を持っていただけましたら幸いです。

この記事が気に入ったらサポートをしてみませんか？