【抜粋】「情報・物理・数理の共創 ~非平衡ダイナミクスの理解が見せる新たな景色~」
国立研究開発法人 科学技術振興機構(略称JST)
から出版されました
「情報・物理・数理の共創 ~非平衡ダイナミクスの理解が見せる新たな景色~」
https://www.jst.go.jp/crds/pdf/2022/SP/CRDS-FY2022-SP-07.pdf
という資料について、再読したついでに、
「個人的に重要だな」と思ったことについて
ご参考として抜粋いたしました( *ˊᵕˋ* )
パラっとご覧になられて、気になったトピックがありましたら
本文をご覧いただけますと、とっても嬉しいです( ⸝⸝•ᴗ•⸝⸝ )
★「情報と物理」という概念について
「一部の学者だけがそう思っている」というわけではなく、
日本や欧米も含めて、【世界規模で大きな流れ】になっている
(お金も動いて、実験も行われている)、
というのが、【本資料での最も重要なポイント】だと思っています(ง'̀-'́)ง
最近では、量子情報の考え方で量子重力を扱うことで、
私たちの宇宙(時空)そのものが量子ビット上の情報から創発する
“it from qubit”
という考え方も登場した。
このように、物理学の概念・手法を
情報学・計算機科学に応用する方向(information is physical)と、
情報学・計算機科学の概念・手法から
物理法則を理解するという方向(physics is informational)の
2つの方向での交流が活性化している。

2.1 現状認識と問題点
(1)情報と物理
情報学や計算機科学と物理学との関係の深化が注目されている。
情報と物理の間の密接な関係は、前世紀からずっと指摘されてきた。
ランダウアの「情報は物理的(information is physical)」という言葉に示される通り、
それまでの物理学が対象としてきた「物質」「エネルギー」に加えて
「情報」も物理法則に従うと考えるのである(図2–1)。
ランダウアはこれをエントロピーを用いて定式化し、
情報処理のエネルギー効率が熱力学第二法則により制限される
ことを導いた(ランダウア原理)[1-4]。
統計力学や量子力学のアイディアが機械学習や最適化などの分野で生かされる場面も多い。
例えば、ニューラルネットワークを用いた機械学習は
スピングラスなどランダム系の統計力学で伝統的に扱われてきたテーマであり[13]、
深層ニューラルネットワークの理論解析に
平均場理論やレプリカ法など物理学の手法・ツールが有効だと知られている14-16]。
これらはいずれも、物理学の概念・手法を情報学・計算機科学に取り入れる方向の流れとまとめられる。
情報理論と非平衡統計力学の融合により、
情報量を熱や仕事などの熱力学量と対等に扱う「情報熱力学」[17]の枠組みが確立
情報を幾何学の視点から考える「情報幾何」は
統計モデルの情報量や推定量の有効性などの
幾何的理解を通して人工知能や機械学習などに貢献[19, 20]してきただけでなく、
熱力学・統計力学[21]や量子情報科学[22]にも大きな影響を与えている。
量子コンピュータや量子暗号・量子通信への応用を中心に発展してきた「量子情報理論」[23-25]は、そのアイディアやテクニックを量子物性や量子重力[6]など物理学の様々な分野との融合でさらなる発展を遂げようとしている[26]。
ここでのキーワードは量子力学的な非局所的相関を意味する「エンタングルメント(量子もつれ)」で、量子計算や量子通信の実現に不可欠なだけでなく、
物性物理における量子多体系やその量子相転移の効果的な表現・解析手法でもある[27-29]。
また重力理論の幾何学的性質にエンタングルメントを結びつける「笠-高柳公式」など、量子重力理論や超弦理論の基礎的な理解にも量子情報理論が有効であると分かってきた[6]。
ホイーラーの「全ての存在は情報から生じる(it from bit)」の言葉を受けた
「時空は量子ビットから創発する(it from qubit)」[5]という考え方も登場し、
基礎物理学における根本的な問題への新たなアプローチ方法として期待されている[30]。
このように、
物理学の概念・手法を情報学・計算機科学に応用する方向と、
情報学・計算機科学の概念・手法から物理法則を理解する
という双方向の交流が活性化しており、今後の発展が期待できる。
(2)熱力学とコンピューティング
情報学と物理学、とりわけ熱力学との関係についての研究の歴史は古く、19世紀まで遡ることができる。
19 世紀末に定式化されたボルツマンの公式はマクロな熱力学量であるエントロピー と統計力学での系のミクロな状態数 と結びつける( はボルツマン定数)最も基本的な式である。
この従来の熱力学が対象とする系は主に熱平衡状態であるため(コラム参照)、一般には平衡状態にない計算機システムの動作と熱力学は無関係だと見なされることも多い。
また、熱力学はすべて1 世紀以上も前の学問で、新たに学ぶことは何もないように思われることもあるが、これらの認識は真実とはかけ離れている。
あまり評価されていないことの一つに、熱力学とコンピューティングの概念的基礎が同じ時期に同じ研究者によって研究され、一方の領域の進歩が他方の領域の進歩を刺激することも多かったということが挙げられる。
例えば、情報理論の父と呼ばれるシャノンは、情報システムの不確実性を説明するために熱力学から「エントロピー」という用語を借りた。
今日のコンピュータの基礎を作り上げた人物としてしばしば挙げられるフォン・ノイマンも、量子力学の数学的な基礎を確立したことで物理学上も重要な人物であり、統計力学におけるギブスエントロピーの量子拡張であるフォン・ノイマンエントロピーにその名を残している。
不可逆的な論理演算に関するランダウアの独創的な研究は「マクスウェルのデーモン(悪魔)」として古くから知られる熱力学的パラドックスにその起源をもつ。
表2–1 に物理学と情報学・計算機科学の歴史の部分的な年表を示した。
本プロポーザルの狙いは、このような双方向の交流を進め、物理学と情報学・計算機科学の双方にとって新しい展開を生み出す機会を創出することである。
情報と物理学を結びつけるきっかけを与えたのは1867 年のマクスウェルによる思考実験である。
マクスウェルは気体分子を1個ずつ観測・操作できる「デーモン」が存在すれば、仕事をすることなく熱力学系のエントロピーを減らすことができ、熱力学第二法則が破れるかもしれないと考えた。
このデーモンと熱力学第二法則の整合性については長らく思考実験を中心に議論が続けられてきたが、
21 世紀に入ってゆらぎの熱力学[31-33]に基づく一般的な理論が構築され、現在ではパラドクスではなくなっている[18]。
現代風に言えば、マクスウェルのデーモンは熱ゆらぎのエネルギースケールで対象の系を測定し、その結果に基づき系にフィードバック制御を行うミクロなデバイスである。
このとき、デーモンが測定によって得た情報のエントロピーと熱力学的なエントロピーの両方を考慮すると、熱力学第二法則を破らないと理解できるのである。
近年、急速に発展している非平衡系の熱力学・統計力学における重要なトレンドは少数自由度のミクロな系の熱力学の研究である。
従来の熱力学が対象としてきたのは主にマクロな系であり、物理量のゆらぎは無視できるほど小さいと仮定される。
ミクロな系ではこの熱ゆらぎの影響は無視できず、物理量が激しくゆらいでいる状況での熱力学を考える必要がある。
実際にこのような状況にある系としては、ブラウン運動するコロイド粒子や生体内の分子モーターなどが挙げられる。
こうしたミクロな系でのゆらぎはランダムに振る舞うように思われるが、実はさまざまな普遍的関係式を満たすことが分かっている。
中でも最も大きな発見はエントロピー生成の普遍的な性質である「ゆらぎの定理」[31, 32]であろう。
ゆらぎの定理は、熱力学第二法則や揺動散散逸定理などを導出できる普遍的な関係式で、
非平衡統計力学にブレイクスルーを与え、先述したとおりマクスウェルのデーモンの現代的な視点からの解釈にも成功した。
ゆらぎの熱力学の考え方を用いて情報量を熱や仕事などの熱力学量と対等に扱う熱力学の枠組みは「情報熱力学」という新しい研究領域の確立に結びついた[17]。
情報熱力学により、これまで平衡状態に対してだけ定義されていた熱力学エントロピーを非平衡状態にも使えるように拡張した「情報エントロピー(シャノンエントロピー)」が導入され、熱力学第二法則は情報量を含む形に一般化された。
情報熱力学により示された情報エントロピーと非平衡熱力学エントロピーの等価性は、マクスウェルのデーモンという物理学の原理的問題に現代的な光をあてただけでなく、情報とエネルギー(仕事や自由エネルギー)の相互変換という新しいデバイスや計算原理とも結びついている。
実際、熱ゆらぎエネルギースケールでの測定・フィードバック制御が可能な実験手法が進展し、コロイド粒子を用いた実験[7]や単電子デバイスを用いた実験[8, 9]など、マクスウェルのデーモンはもはや思考実験上の存在ではなくなった。
情報の概念抜きでは非平衡統計力学を語れないのと同時に、非平衡統計力学抜きには情報処理を語れないと言える。
このような非平衡系の熱力学・統計力学の最近の理論的進歩を計算を結び付けることは、本質的に新しい計算原理や低エネルギーの情報処理デバイスの設計指針などを生み出す可能性がある。
(3)量子情報の発展
量子情報科学は、量子力学、計算機科学、情報理論、計算複雑性などを含む
物理と情報にまたがる学際的な融合分野である。
エンタングルメント状態における非局所相関などの量子論特有の現象について理論・実験的にアプローチする物理学的な研究と、その結果を通信や情報処理に応用する工学的な研究の両面を持つ分野である。
主要な研究テーマには量子コンピュータ、量子暗号鍵配送、量子通信、量子センシングなどが挙げられる。
量子情報とは、量子状態がもつ情報(および量子状態そのもの)を指す言葉だが、現在ではその操作による情報処理までを含む量子情報科学・工学分野を現す言葉として用いられることも多い。
量子力学は微視的なレベルでの物質の特性を扱うが、量子情報科学はそれらの特性にエンコードされた情報を扱う情報科学である。
量子計算は、このような量子情報を操作・処理することで論理演算を実行することにほかならない。
情報を取得する最も基本的な方法は測定(観測)だが、不確定性原理により非可換な2つの物理量を同時に正確に測定することはできないことが量子系から取り出しうる情報量に古典情報理論とは異なる制約を与えている。
古典情報理論におけるシャノンエントロピーに対応し、量子情報理論では密度行列のフォン・ノイマンエントロピーを情報量の基本的な尺度として用いる[22, 25]。
また、量子情報における重要な概念のひとつがエンタングルメント(量子もつれ)である。
エンタングルメントは古典系では実現できない量子力学特有の相関で、量子計算や量子通信など量子情報処理の本質的なリソースだと考えられている。
エンタングルメントを使うと特殊相対性理論の光速度不変の原理に一見反するかのような状況を作り出せるため、量子力学の黎明期には重大な欠陥として論じられたが現在では解決されている(=超光速の情報伝達はできない)。
このパラドックスは長らく思考実験として議論されてきたが、「ベルの不等式」(CHSH 不等式)として実験検証できる形に一般化され、ついにはアスペらによりベル不等式の破れも実験検証された(2022 年のノーベル物理学賞の対象にもなった)。
また、これらの社会・経済的課題の解決に加え、量子情報は新しい学術分野の誕生にも貢献すると期待されている。
エンタングルメントや量子計算等の量子情報理論の概念を量子物性や量子重力に応用する研究潮流が世界的に活性化しており、大きなインパクトを持つ成果も上がり始めている。
量子物性への応用では、量子計算複雑性と物質の新たな量子相の特徴づけとの関係、量子誤り訂正符号とトポロジカル物質中のマヨラナ粒子など量子情報的な考え方や手法はこの10~20 年間の量子物性理論の発展に大きな影響を与えてきた[27]。
量子重力への応用では、エンタングルメントエントロピーを用いて超弦理論と量子情報理論の関係性を深化させた「笠ー高柳公式」の発見や、量子テレポーテーションや量子誤り訂正符号を用いたブラックホール情報喪失問題へのアプローチなどが注目されている[6, 30]。
(7)問題点
情報熱力学の言葉でコンピューティングパラダイムを再構築することは、
物理世界のすべてのプロセスが自由エネルギーの散逸によって駆動される
という認識から始まるだろう。
有限の時間での状態の遷移(=情報処理)は、非平衡な物理プロセスだが、
現在のパラダイムでは一種の数理的な状態遷移プロセスと見なされてしまっている。
そのため、熱力学がもたらす速度限界や有限時間で状態を変化させることに伴う熱力学的コストとのトレードオフは、論理のレベルにはほとんど反映されていない。
量子コンピュータの場合には、エネルギー散逸に加えて状態遷移が本質的に確率的であることも考慮する必要がある。
このように現在の情報学・計算機科学では、熱力学はエネルギー効率の高いハードウェア設計や効果的な熱除去を動機付ける工学的な制約と見なされているが、本来はソフトウェア階層や計算原理にも熱力学的な考察が必要である。
低エネルギーの情報処理システムの実現には生命システムからのインスピレーションも極めて重要だろう。
動物、植物、バクテリアなど、複雑な資源制約下で繁栄できるのはエネルギー効率の高い構成や状態変化を自発的に見つけた種である。
自然計算としてはタンパク質の折り畳みも参考になろう。
これらのシステムのほとんどは非平衡系であり「情報」の概念でそのダイナミクスを理解し直すことで、その計算能力を将来のコンピューティングシステムに利用できる形に翻訳できるものと期待される。
包括的な科学的課題は、量子系まで含めた非平衡系における散逸、ゆらぎ、平衡化、測定、制御などを「情報」の観点から理解し、新しいコンピューティングパラダイムへとつなげていくことである。
そのためには現在までに構築されてきた物理学と情報学・計算機科学との交流を、より一層洗練させ、深化させていく必要がある。
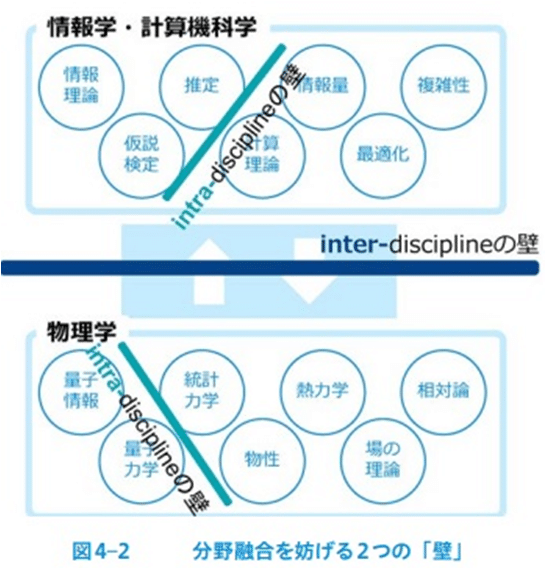
そのために最も深刻な課題となるのは、研究コミュニティ間の交流が限定的であることだろう。
多くの研究開発課題は情報学・計算機科学と物理学の間や、量子情報と統計力学の間など、分野やコミュニティを跨がった取り組みが不可欠である。
そのため、問題意識の共有や議論が行える場が必要である。
異分野連携・分野融合に関連する推進上の課題の詳細は4章で述べる。
2.3 科学技術上の効果
本プロポーザルで提言する研究課題・推進方策を実行することで、
物理の概念や手法で情報・計算を扱う研究者と、
情報理論の数理から物理法則を理解しようとする研究者の
双方向の交流がますます活性化し、既存学問分野の垣根を超えた
「情報・物理・数理の革新的融合領域」
と言える 【新たな学際領域】 が形成される。
物理学を中心に量子から生物まで非平衡系のダイナミクスにおける新しい理論的枠組みや実験的検証手法が多数見いだされ、計算機科学ではコンピューティングパラダイムの革新も期待される。
これまでの物理学では閉じられた平衡系を扱う理論的枠組みしか存在せず、そこから大きく外れる非平衡系は議論することが困難であった[18]。
例えば、非平衡系は、平衡系からの外れを1 次の微小量とみなしてよい線形非平衡系と、この近似が許されない非線形非平衡系に大別されるが、これまでの物理学では主に線形非平衡系を扱う理論的枠組み(線形応答理論など)しか構築されていなかった。
しかし、コンピュータをはじめ世の中に存在するデバイスは(ほぼ)全てが非平衡系であることから、本プロポーザルの提言内容を実行することで、既存の線形応答を超える非線形の強い領域まで扱える理論的枠組みが構築されることが期待される。
また、その過程で新概念の発見や新現象の理論的予測・実験的検証が相次ぐことが期待される。
情報量を熱力学量と対等に扱う「情報熱力学」もさらなる発展を遂げ、情報処理に必要なエネルギーの原理的限界値や新たな省エネルギーデバイスの設計指針を予言できるようになる。
低エネルギーの情報処理システムの観点からは、最もエネルギー効率が高いと言われている生命システムとの繋がりも重要となり、生物物理学やシステム生物学との連携・融合も期待される[69, 70]。
ここでは、情報熱力学の理論的枠組みを活用することで生命現象の理解を深め、生命システムの設計原理を解明することが期待される。
同時に、生命現象を具体例として情報熱機関の設計原理を議論することで情報熱力学の深化や非平衡ダイナミクスを扱う理論的枠組み、実験的検証手法の開発の進展にも繋がることが期待される。
加えて、情報熱力学を量子系にも適用することで、量子コンピューティングの熱力学における未解明な課題にもアプローチ可能となり、実用性のある量子コンピューティングを実現するための新しいデバイス構造の予測・実現にも貢献することができる。
このように、本プロポーザルに記載されている研究課題や推進方法を実行することにより、古典系のみならず量子系を含めた非平衡ダイナミクスにおける散逸、ゆらぎ、平衡化(熱化)、測定、制御などを「情報」の観点から理解することが可能になり、新しいコンピューティングパラダイムを創出することができる。
また、情報学・計算機科学と物理学の間や、量子情報と統計力学の間など、分野やコミュニティを跨った取り組みが活発化するだけでなく、生物物理学やシステム生物学など幅広い学問分野なども含めた多様な学問間での問題意識を共有・議論を行える場が形成され異分野連携・分野融合が加速される。

しかし、ランダウア原理も、特定の形状のメモリのモデルに基づいたものであり、実際に、2009 年になって沙川と上田により、非対称メモリを用いることで仕事なしで情報消去が可能になると指摘されている。
また、沙川らはゆらぎの熱力学などに基づいて、デーモンに要する仕事についての一般的な関係式を導いた。
それによると、測定に要する仕事と消去に要する仕事には一般にトレードオフがあり、両者の合計Wdemon の下限が相互情報量I を用いてWdemon ≥ k BTI で与えられる。
すなわち、測定と消去を合計してはじめて仕事の普遍的な下限がある。
k BTI は測定で得た相互情報量に由来しており、
情報を取得する際、余分に必要な仕事がデーモンに要する仕事の起源である。
このような議論によって、デーモンと熱力学第二法則の整合性が現代的に理解されると言える。
ランダウア原理の議論は、シャノン情報量を環境に捨てるときに必要な仕事についてであり、
相互情報量についてではない点に注意が必要だ。
※注:つまり「環境への廃熱に必要な仕事(古いランダウアの原理)」ではなくて、相互情報量のほうが本質(新しい沙川・上田の情報熱力学)。
3 具体的な研究開発課題
「ゆらぎの定理」[31,32]、「予測の熱力学」[71]、「情報熱力学」[17,18,72]などの物理学上の概念やツールを用いて、情報処理の熱力学的コストと計算速度とのトレードオフの理解が欠かせない。
機械学習への応用も期待される。
とりわけ統計力学は歴史的にもニューラルネットワークと深い関係があり、非平衡統計力学における発見はニューラルネットワークによる学習の理解や、新たな手法開発に応用できる可能性が高い。
物理学そのものを深化し発展させることは、結局は情報学や計算機科学を発展させることにつながる。
量子力学と情報理論が融合した新たな分野である量子情報科学の考え方を物理学の様々な分野に逆輸入することは極めて有用だと考えられる。
例えば、リソース理論の考え方を熱力学に応用した熱力学リソース理論や、
量子計算複雑性の考え方を用いた物質のトポロジカル量子相の分類など、
いくつかの分野ではすでに有効性が示されている。
このような物理学と情報学・計算機科学の交流を深める上での共通言語は数学であろう。
「3.3 物理学と情報学・計算機科学をつなぐ数理基盤を構築する」では
微分幾何、位相幾何、非可換幾何に着目する。
3.1 物理学の概念・手法を情報学・計算機科学に応用する
(1)情報熱力学による計算エネルギー効率の解明
情報の消去に関するランダウア限界を一般的な情報処理における散逸にまで拡張した「情報処理の第二法則」[73,74]の試みは、コルモゴロフ・シナイエントロピーで測定される情報生成が中心的な役割を担っている点を指摘している。
これは、与えられた量の計算を進めるために供給しなければならないエネルギーの最小量を与えるもので、「情報」が熱力学的リソースであることを意味している。
総じて、早く・正確に状態を変化させるには十分なエネルギー散逸(熱力学的コスト)が必要であり、様々な熱力学的トレードオフ関係の理解と、その計算機科学への応用が極めて本質的で重要な研究開発課題である。
そもそも、従来の(マクロな)熱力学には「スピード」の考え方はなく、熱機関の理論的限界であるカルノー効率を有限時間の操作(つまりカルノーサイクルが仮定する準静的な過程ではない過程)で達成できるかどうかは長い間の未解決問題であった。
直感的には、準静的過程以外でカルノー効率を達成するのは不可能に見えるのだが、その証明がなかったのである。
【ゆらぎの熱力学】を用いた効率とスピード間の普遍的トレードオフ関係の証明[77,78]を通じ、カルノー効率と有限の仕事率(パワー)が両立しえないと分かり、ようやく熱力学にスピードの考え方がもたらされた。
このような状態変化と熱力学的コストのトレードオフ関係は「速度限界(speed limit)」とも呼ばれ、近年精力的に研究が進められている。
状態を大きく変化させるような場合(【局所詳細釣り合い】を満たさない場合)については、
標準のエントロピー生成の代わりに波多野-佐々エントロピー生成を用いることで
状態変換の速度とエントロピー生成の間のトレードオフ関係(不等式)を一般化
できると報告されている[79]。
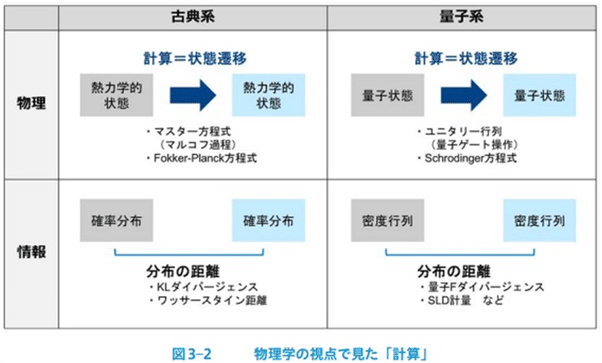
計算機の熱力学的状態の変化とは計算(情報処理)そのものであり、
計算速度や正確さが消費電力とトレードオフ関係にあることと直接対応している。
熱力学的な状態を確率分布とみなせば、その遷移をフィッシャー計量を用いた情報幾何学や、ワッサースタイン距離を用いる最適輸送理論などの枠組みで扱うこととの親和性の高さも理解できる[20, 21]。
実際、情報幾何学と速度限界・熱力学的不確定性関係[80]や、ワッサースタイン距離と熱力学的速度限界[81]、2 つの分布間の距離を熱力学的不可逆性の度合いを使って解釈する関係式[82]など、情報幾何学と熱力学の密接な関係からさまざまな発見が得られている。
熱力学的コストや熱ゆらぎを抑えながら熱力学に最適な状態変化を考えることで、省エネルギーな計算原理や、新しいアーキテクチャにつながるものと期待される。
同様の議論は量子コンピュータに対しても展開することができ、その場合には「状態」とは複数の量子ビットから構成される量子多体系の量子状態のことを指す。
熱力学と異なり量子力学にはハイゼンベルグの不確定性原理という形で速度限界の議論がもともと埋め込まれているが、情報伝播に与える制限としてはリープ・ロビンソン限界が知られている。
この限界が現実の量子コンピュータでの計算速度に与える影響の評価や、この限界を考慮した量子回路の設計などは挑戦的な課題である。
量子版「マクスウェルのデーモン」のような設定から始め、量子系における情報の熱力学の一般的な理解の確立が求められる。
量子力学の不確定性原理は、熱力学の速度限界とも深い関係にある。
量子版の速度限界である時間とエネルギーの不確定性関係(の一つの表現)は量子情報幾何における量子フィッシャー情報量を用いた「量子クラメール・ラオの不等式」の特殊な場合であり、これは(古典)情報幾何学におけるフィッシャー情報量による速度限界の量子版拡張と見なせる[84-86]。
情報幾何学と量子情報幾何学の重要性については3.3節で述べる。
(2)非平衡統計力学の機械学習への応用
深層ニューラルネットを用いた教師なし機械学習については、教師あり機械学習に比べてさらに理論的に未成熟の状況である。
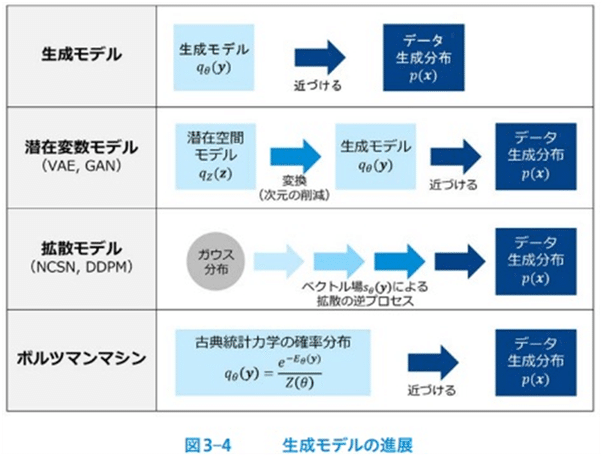
物理学と関係が深く、古くから用いられている確率モデルはボルツマン分布に基づくボルツマンマシンであり、直接的にイジングスピンモデルにマップできる。
ボルツマン形式の確率分布を用いると、対数尤度を最大化する学習プロセスは、モデル分布の全体的な自由エネルギーを増加させながら、観測されたデータのエネルギーを最小化することに対応付けられる(カルバック・ライブラー情報量はギブスの自由エネルギー差と対応する)。
このようなエネルギーベースのモデルは現在でも生成モデルに積極的に用いられている[97]。
制限ボルツマンマシンはエネルギー関数の学習に課題を抱えていたが、近年、ランジュバン方程式(統計力学において、あるポテンシャルの下でのブラウン運動を記述する確率微分方程式)を用いる新手法の提案がなされ注目されている[98]。
情報理論や計算理論が扱う問題に統計力学の概念やツールを用いてアプローチする情報統計力学も極めて関連が深い分野である。
統計力学がこれまで対象としてきたガラスやスピングラスなどの系の自由エネルギーランドスケープと組合せ最適化問題の利得ランドスケープは似ていると考えられており、組合せ最適化問題の解析や、それに対する近似アルゴリズムの性能評価(精度や収束の速さ)に統計力学の手法が用いられている[13,99]。
周辺分布を計算する近似アルゴリズムである確率伝搬法も物理に着想を得たものとされている。
非平衡統計力学と機械学習をつなぐ研究は、両方の分野に利益をもたらす可能性が高い。
有望な方向性として、物理システムを情報処理エンジンとして扱うアプローチが考えられる。
特に注目されるのは、非平衡熱力学に基づく生成モデル(拡散確率モデル)の発展である[100]。
2020 年に提案されたデノイジング拡散確率モデルでは、変分オートエンコーダー(VAE) や敵対的生成ネットワーク(GAN) ベースの画像生成AI を超える高精度の画像を生成できることで大きな注目を集めた。
2022 年に発表された潜在拡散モデル[101]は拡散プロセスをピクセル空間ではなくVAE の潜在空間で実行することにより、画像生成の処理を高速化した。
個人のPC でも動作するモデルをオープンソース「Stable Diffusion」[102]として無料公開したことでも話題を呼んだ。
現在の理論的理解は今後数年間で出現する、より統一された全体像からすると氷山の一角にすぎないだろう。
しかし、この目に見える小さな部分でさえ、深層学習の理解と新展開におけると統計力学アプローチの有効性を明らかにしたことは特筆に値する。
深層学習の理論解析では、ここに挙げたランダム系の相転移、カオス、スピングラス、ジャミング、ランダム行列などの統計力学における概念や手法だけでなく、後述する情報幾何などの数理科学的なアプローチも重要である。
コラム 効率と仕事率
カルノー効率を達成しつつも仕事率がゼロでないような熱機関は存在しないことが分かっている[77]。
この結論は量子・古典を問わず成立するが、量子の場合にはこの制限を実効的には無効化できることが近年報告され話題となっている[103, 104]。
論文では、量子効果を適切に用いることで、カルノー効率を漸近的に達成しつつ仕事率がゼロでないプロセスの存在が示されている。
3.2 情報学・計算機科学の概念・手法を物理学に応用する
(1)量子情報理論の熱力学への応用
大規模な量子状態を精度よく作成したり、それを誤りなく遠方へ伝送したりする量子技術の水準がまだ実用化レベルに達していないのである。
これらの技術的な制限を動機に生まれたのが「リソース理論」と呼ばれる量子情報理論の考え方である。
リソース理論は、制限された物理操作の下での量子情報処理を考える枠組みで、「ある状態を別のある状態に遷移させる際に、フリーな(=コストを払わずにタダで手に入る)操作や状態とは別にコストのかかるリソースがどのくらい必要か」といった問題を扱う。
フリーな操作やリソースの定義は、リソース理論を何に適用するかに依存し、たとえば「エンタングルメントのリソース理論」では、実装が容易であると見なされる局所操作と古典通信(LOCC)をフリーな操作、エンタングル状態をリソース状態として秘密鍵の共有などのタスクを実行するのにどれだけのリソースが必要かを見積もる[105]。
フリー操作は量子力学が許容するすべての物理プロセスを網羅しているわけではなく、ある制約条件の元で実現可能な特定の量子状態のみを準備できる。
このようにフリー操作によって作ることができる状態はフリー状態、そうでない状態はリソース状態と呼ばれる。
したがって、リソース理論はすべての操作と状態を「フリー」か「禁止されている(=リソース)」かに分類した上で、制約条件のもとでのリソースの使用を考える理論枠組みと理解できる。
エンタングルメントのリソース理論の他にもコヒーレンスのリソース理論や、対称性のリソース理論など、様々なリソース理論が提案され、その考え方は量子情報の研究コミュニティに急速に広まっている[106,107]。
量子情報科学で生まれたリソース理論の考え方を熱力学に応用する「熱力学リソース理論」[108]という新たな分野も生まれた。
リソース理論の考え方は熱力学における基本的問題のいくつかに新たな光を当てる研究へと繋がり、熱力学の基本法則の情報理論的な理解を深化させる研究が活発に行われている[109-111]。
熱力学リソース理論における典型的な設定は、「熱浴と相互作用して時間発展する操作」をフリー操作とし、「外部に対して仕事をできる状態」をリソースとする。
フリー操作によって実現可能な状態はボルツマン分布(ギブス分布)である。
したがって熱力学リソース理論では、注目している系の初期状態が熱浴に触れて時間発展し、終状態に達する場合に外部(リソース)からどれくらい仕事をされるか(または、外部にどれだけ仕事をするか)を考えていることになる。
熱力学へのリソース理論アプローチは、熱力学の適用範囲をミクロ系に拡張するだけでなく、熱力学第二法則に関わる数理構造を情報理論の観点から整理することにも成功した。
さまざまなリソース理論の中で熱力学との関連が深いものに「非対称性のリソース理論(resource theoryof asymmetry)」がある。
これは、ある保存則を満たす操作をフリー操作とし、リソースを使ってどれほど保存則を破る操作(保存量の異なる固有値を持つ固有状態への遷移)ができるかを、異なった保存量をもつ固有状態間の量子コヒーレンスに注目して考える枠組みである。
物理的操作は基本的にはエネルギー保存則を満たすので、熱力学の操作もこのコヒーレンスに関する制約を受けているはずである。
実際に、量子系では熱的操作(ギブス状態の補助系とエネルギー保存則を満たす写像)はギブス保存写像(ギブス分布をギブス分布に移す写像)よりも狭いクラスの操作だと知られている。
コヒーレンスに関する制約は、コヒーレンスの蒸留が不可能であること[112]や、触媒を用いてもインコヒーレントな初期状態にコヒーレンスは作れない[113,114]という結果が得られている一方で、何度でもリサイクルできる外部系[115]や複数の相関した触媒[116]などの利用によりどんな状態変換も可能になるという結果も報告されている。
他にも、保存則や対称性が量子ゲートの実装や量子誤り訂正符号、ブラックホールからの情報脱出などに与える制約を解析でき、非対称性のリソース理論は本プロポーザルで扱う様々な対象に統一的な視点を与えうるものとして注目される[117-120]。
今後、相互作用する多体系などの現実に近い系についての理論・実験両面からの熱力学リソース理論の研究が必要である。
熱ゆらぎのエネルギースケールでのミクロな系の非平衡熱力学や情報熱力学に加え、量子力学的に相互作用する多体系(量子多体系)の熱力学への応用も求められる。
おそらく最も初期の重要な貢献のひとつは、ジェインズによって導入された最大エントロピー原理だろう。
ジェインズは、情報理論のツールを使用して微視的な力学的法則(古典・量子)から統計力学の方法を正当化する問題に取り組んだ。
実際、量子力学から熱力学・統計力学を導き出す試みは、フォン・ノイマンの研究から始まる量子力学自体とほぼ同じくらい長い歴史を持つ。
現在でも進行中の活発な研究分野であり、量子情報コミュニティからも注目を集めている。
従来、ミクロな古典力学からマクロな熱力学を導出するには統計力学を経由することが一般的であった。
ミクロ系の熱力学であるゆらぎの定理から熱力学第二法則を導出する過程でも、熱浴の初期状態にカノニカル分布(統計力学の概念である)を仮定するなど、やはり統計力学を経由することでミクロな量子力学とマクロな熱力学を結びつけていた。
しかし、実際の熱浴は必ずしもカノニカル分布をしているとは限らないため、量子力学から直接(=統計力学を経由せずに)熱力学を創発しようという研究が近年精力的に進められている[121,122]。
特にその焦点となっているのは時間反転に対称な(可逆な)量子力学から、どのようにして時間の向きをもつ(不可逆な)熱力学第二法則が現れるのかという問題である[123]。
従来の統計力学を経由するアプローチではなく、量子力学だけから熱力学を導出する際の鍵となるのが量子状態がどのようにして熱平衡状態に緩和するかという「熱平衡化(熱化)」の理解である。
とりわけ、環境から切り離された孤立量子系がシュレーディンガー方程式に従って時間発展したときにどのように熱平衡化するか、理論・実験の両方のアプローチでの研究が精力的に進められている[124]。
イオントラップや冷却中性原子などの量子シミュレータ技術が発展し、さまざまな量子多体系の現象を精度良く制御できる実験環境が整ったことも背景にある[125]。
熱平衡化を説明するメカニズムとして注目されている考え方は「固有状態熱化仮説(EigenstateThermalization Hypothesis, ETH)」である[123, 126]。
ETH は量子多体系の全エネルギー固有状態が熱平衡状態を表すとする仮説で数学的な証明もないが、いくつかの系では成立していることが数値計算により確かめられている。
また、ETH と量子多体系での情報の伝搬速度の上限である「リープ・ロビンソン限界」という量子情報の概念と組み合わせることで、熱浴の初期状態が(統計力学のカノニカル分布ではなく)量子力学のエネルギー固有状態の場合にも熱力学第二法則とゆらぎの定理が短時間では成立することも数学的に証明されている[122]。
ETH により統計力学を経ずに量子力学から熱力学を直接導き出すシナリオが明らかになりつつあり、今後、孤立量子系の熱平衡化のメカニズム解明は飛躍的に進むものと期待される。
またETH のみでは熱平衡化が説明できないと示唆する結果も報告されており、多体局在状態(Many-bodyLocalization 状態)[127,128]や量子多体傷跡状態(Quantum Many-body Scar 状態)[129,130]など熱平衡化しない量子状態が注目されている。
このような非平衡量子相は、対称性の破れで特徴づけられる平衡状態とは異なる新しいタイプの量子相と考えられ、離散時間結晶(Discrete Time Crystal)[131,132]などを含め相転移の観点からも精力的に研究が進められている。
非平衡量子相はエンタングルメントエントロピーの時間発展などで特徴づけられ、近年では様々な実験検証も報告されている。
冷却原子や超伝導量子ビットなどの人工量子系(量子シミュレータ)を用いて探索が進められている新しい非平衡量子相やそのダイナミクスは、将来的な量子情報処理のプラットフォームに繋がると期待される。
最先端の量子技術の研究開発には、ETHや熱平衡化のような基礎学理的な問いを深め量子多体系の非平衡ダイナミクスを理解することが極めて重要である。
(2)量子情報理論の量子物性への応用
量子情報の考え方や手法は物理学全体に急速に浸透しつつあり、物理学と情報学・計算機科学が融合した新しい領域の開拓が進んでいる。
とくに、物性物理学における量子系の現象を量子情報の観点から捉えることで、トポロジカル量子相の理解の深化やテンソルネットワークを用いた数値計算手法の発展など物性理論を中心に数多くの基礎物理で進展が見られた[27]。
近年では、場の量子論を通じた素粒子物理学や重力理論、超弦理論との交流も進んでいる[6,30]。
物性物理学における最も基本的で重要な問題は相の分類である。
これまで、ランダウ理論に始まる対称性の自発的破れや秩序パラメータなどの概念による分類が多くの成功を収めてきた。
統計力学では相転移は系の対称性の変化だと理解でき、絶対零度での相転移である量子相転移も自発的な対称性の破れによって説明できると考えられていた。
しかし、分数量子ホール効果(図3–5 左下)の発見を皮切りに対称性を保ったまま量子相転移が生じる系が見つかり、新しい相分類方法が求められていた。
とくに「トポロジカル秩序相」と呼ばれる量子相は、縮退した基底状態はどれも対称性を破っておらず通常の秩序パラメータでは特徴づけができない。
また、対称性の下でのみ自明な相と区別される「対称性によって保護されたトポロジカル(SPT:Symmetry-Protected Topological)相」(図3–5 右下)の特徴づけも重要である。
これらの物質の量子相の分類は長年物性理論の研究者を悩ませてきたが、量子情報理論におけるエンタングルメントや計算複雑性の考え方が輸入されると極めて見通しよく理解されるようになった[27]。
量子相を特徴づける方法はいくつかあるが、例えば積状態などの自明な状態から定数深さの量子回路による操作で対象となる量子状態が作れるかどうかで量子相を分類する方法がある。
基底状態がトポロジカル秩序相かどうかを判断するのに、複雑性を測る指標であるトポロジカル・エンタングルメント・エントロピーが用いられるのも好例といえよう[133,134]。
トポロジカル秩序相は理想的な量子情報処理プラットフォームとしても注目されている。
これは、トポロジカル秩序を持つ2 つに縮退している量子状態は、どのような局所的摂動に対してもその縮退が解けず、対称性も破れないため、それらの重ね合わせ状態が外乱に対してロバストに保持される性質による。
トポロジカル秩序を記述する具体的なモデルとしてはキタエフのトーリック符号モデル[135]が知られているほか、二体相互作用から構成されるマヨラナモデル[136]やハニカムモデル[137]も提案されている。
量子回路複雑性のほかにも、複雑性クラスや決定可能性など計算複雑性理論の概念や手法をより直接的に物理に持ち込む研究も盛んに行われている。
例えば、ある量子多体系を表すハミルトニアンが与えられたときに、その基底状態と第一励起状態の間にエネルギー差(ギャップ)があるかどうかを決める問題は決定不可能だと示されている[138,139]。
また、そもそも基底状態のエネルギー固有値を求める問題はクラスQMA という(量子コンピューターでも効率よく解けない)難しい問題だと知られている。
多体局在状態や量子多体傷跡状態など熱平衡化しない量子多体系があることは先述したが、このような与えられた孤立量子系が熱平衡化するかどうかを判定する問題も決定不可能だと近年示された[140]。

量子情報の考え方を用いた量子物性物理と量子情報処理のための量子技術は、量子状態の変化を情報処理として理解するか利用するかというモチベーションの差にすぎず、その本質は量子情報を共通言語とした物理学である。
量子誤り訂正符号や量子回路複雑性をきっかけとした量子情報と量子物性の交流は今もなお続いており、今後も量子相の理解の深化や新奇物性の予言と実験検証が期待できる。
トポロジカル符号による誤り耐性量子計算は、量子ビットの二次元配列を用意してその上にトーリック符号(表面符号)を実装するという量子情報アプローチと、物質のトポロジカル秩序相で実現されるマヨラナ準粒子を制御するという量子物性アプローチの両面から研究が進められている[142]。
実際、量子シミュレータを用いたエンタングルメントエントロピーの測定[145,146]や、多重局在状態、量子多体傷跡状態、離散時間結晶などの非平衡量子相の量子シミュレーション[128,130,132]が報告されているほか、超伝導量子コンピュータ用のチップを量子シミュレータとして用いることも試行されている[147]。
量子多体系の動的な性質(ダイナミクス)の研究は量子物性系が量子情報をどのように処理・伝達しているのかを明らかにすることに直結し、量子情報処理の原理の理解が深まると期待できる。
量子物性・量子情報のどちらのアプローチをとるにせよ、実験による研究が重要である。
単なる理論予測の検証を超えた、理論と実験の両輪での研究開発推進が望まれる。
量子重力理論におけるホログラフィー原理や、時間に依存する系への相対エントロピーの応用も盛んに議論されている。
反ドジッター時空(AdS)上の重力理論と、その境界上に住んでいる重力を含まない共形場理論(CFT)が等価になることを主張する「AdS/CFT 対応」は、共形場理論から重力理論が創発することを示唆する。
エンタングルメント・エントロピーが重力理論の宇宙における曲面の面積に等しいことが分かり[148]、量子エンタングルメントから重力理論の宇宙が創発するという考え方が生まれ注目されている[6]。
さらに、共形場理論における相対エントロピーを使うことでAdS 時空上の重力のダイナミクスを読み取れることがわかりつつある。
テンソルネットワークとの関係も指摘されている。またブラックホール情報喪失問題において「スクランブリング」とよばれる、熱平衡状態における量子情報の急速な脱局所化現象が本質的な役割を果たすことがわかり、この現象を検出する手段としての相対エントロピーの有用性も指摘されている[149]。
物理学ではこれまで、素粒子・宇宙・物性など縦割りに分野が分かれて研究が行われてきた。
しかし、近年量子情報の考え方がこれらの分野に横串を通し、宇宙創成から量子物質までさまざまな物理学の重要な研究対象の難問を解決する鍵となることが分かってきた。
量子物性に見られたような進展と全く同じような進展が、量子重力の研究でも見られており、量子情報の言葉を使いこなす事は前提知識となっている。
今後、量子情報は、現代物理学を研究する上での「文法」あるいは「常識」のようになり、各分野に組み込まれていくだろうと考えられる。
3.3 物理学と情報学・計算機科学をつなぐ数理基盤を構築する
(1)微分幾何の展開
微分を利用した幾何学である微分幾何学の重要な対象は多様体であり、計量によって局所的にユークリッド空間と同じように扱うことができる。
情報幾何学は確率分布の空間に構造を導入することで、確率分布を扱う様々な分野の問題に統一的な視点を与える。
情報幾何学が対象とする多様体は、確率分布全体のなす多様体である統計多様体であり、フィッシャー計量の導入により確率分布間の違いや統計的性質を測ることができる[19]。
情報幾何学の考え方を用いることで統計学における統計モデルの情報量や統計量の十分性、推定量の有効性など様々な概念の統一的理解が得られるようになったばかりでなく情報理論や信号処理、近年では機械学習にも大きな影響を与えてきた[20]。
前節までで述べたように、物理学から見た情報処理は熱力学的状態(統計力学では確率分布で記述される)の遷移であり、これは明らかに情報幾何学の枠組みと整合している。
実際、熱力学でのエントロピー生成率がカルバック・ライブラー情報量を用いて記述されたり、確率過程で記述される熱力学的ダイナミクスを理解する上で時間に関するフィッシャー情報量(情報幾何学における確率単体上の速度の指標)が重要となったり、ミクロな系の熱力学(ゆらぐ系の熱力学)の法則の背後には情報幾何学の視点が自然な形で埋め込まれていることが知られている[21]。
非線形力学系や化学反応ネットワークなど、これまで情報幾何学がアプローチしてこなかった熱力学・統計力学上の問題はまだ無数にあり、これらの問題への情報幾何学の視点の導入は、情報幾何学にも新たな展開をもたらしうると考えられる。
情報幾何学は、今後も物理学と情報学・計算機科学の間の共通言語的な役割を担うと期待される。
情報幾何学の量子版である量子情報幾何学もまた長年にわたり研究され、現在も発展を続けている分野である。
量子力学の数学的体系は確率論の拡張とみなすことができ、量子状態全体のなす多様体にフィッシャー計量の類似を導入することができる。
従来の情報幾何学ではフィッシャー計量がただ一つのリーマン計量だったのに対して、量子情報幾何学では多くのリーマン計量が定義できる状況にあり、問題ごとに個別に定義される幾何構造に対して統一的な描像が得られるかという問題がここ20年の大きな課題となっている[22]。
従来の情報幾何学と量子情報幾何学の差異は量子力学がもつ作用素の非可換性に起因しており(量子状態を表す密度行列は数学的には半正定値行列で表現される)、情報幾何学での双対平坦構造が量子情報幾何学ではなくなることで幾何学として複雑な構造を持つと理解される。
量子版に拡張することの情報理論的な差異は、統計的推定理論にも現れる。
例えば、従来の統計学でのパラメータ推定問題では、クラメール・ラオ定理によりフィッシャー行列(の逆行列)が局所不偏推定量の共分散行列の達成可能な下界を与えていたが、量子版では推定量の非可換性のためにそのような共分散行列の達成可能な下界というものが一般には存在しないことが知られている[22]。
このように量子情報幾何学と量子推定理論、量子情報幾何学と不確定性原理など、量子状態の遷移や量子計算という共通の現象を別々の視点から見たときにどのように対応付けられるか、相互関係を精緻に明らかにしてゆく方向の研究が必要であろう。
最適輸送理論も、情報学・計算機科学と物理学の間をつなぐ普遍的な考え方を提供すると考えられる。
とりわけ統計力学の問題設定の多くは、数理的には最適輸送理論で扱える。
最適輸送理論は、複数の工場と複数の店舗があったときに商品を運ぶためのコストを最小にする方法を求めるという理論枠組みであり、連続の場合には確率分布の間の「移動」を最小にする最適化問題に帰着する。
確率分布の間の距離を測るのがワッサースタイン距離である(カルバックライブラー情報量とは異なり、ワッサースタイン距離は距離の公理を満たす)。
今後は、統計学や機械学習でこれまで多く用いられてきたフィッシャー計量とワッサースタイン計量を適切な設定のもとで統一的に扱う「ワッサースタイン情報幾何学」ともいうべきフレームワークの構築が必要である。ワッサースタイン計量とフィッシャー計量とをつなげることは、そのまま情報学と物理学をつなげることに直結している。
そのような俯瞰的理論である「ワッサースタイン情報幾何学」の創造に向けた取り組みは、情報学や物理学だけでなく、数理科学上の重要な発見を生み出す可能性も秘めている。
情報幾何学や最適輸送理論はいわば情報の幾何学であり、実際、機械学習(EM アルゴリズムやワッサースタインGAN、深層生成モデルなど) に応用されている[20]。
深層生成モデルの一種である拡散モデルは非平衡統計力学のアイディアに基づいたもので、画像生成モデルStable diffusion に用いられている[101]。
さらに熱力学的な状態遷移をこれらの2つの幾何学で捉えることで、熱力学のコストと正確性やスピードとのトレードオフが得られる。
ここでは、古典と量子の間に考えうる省エネルギーな熱力学的コンピューティングの設計という研究の方向性がある。
このような意味で物理学と情報学・計算機科学の幾何学の相補的な発展が期待できる。
教師あり機械学習のひとつであるベイズ学習は、代数的構造と多様体という幾何的構造を兼ね備えた「リー群」を利用することで改良できると期待されている。
例えば、ベイズ学習におけるアップデートルールは全て統計多様体上の最急降下法で説明されるが、一部分で微分幾何的におかしな操作をしている。
ここにリー群からの作用を入れパラメーター付けをすることで克服が可能だと知られている。
リー群からの作用はさまざまなものがあり、より表現力の高い学習を目指したリー群の考え方の機械学習への適用研究が重要である。
(2)位相幾何の応用
統計力学を数学的に基礎づける手法の一つである流体力学極限1において、ミクロモデルの汎用的記述に対するコホモロジーを用いた解析により、保存量の定式化や群作用の役割の抽出、相互作用の局所性が果たす役割の抽出など様々な理解が得られており[150]、今後も数学的理論の発展が望まれる。
理 化 学 研 究 所に設 立された数 理 創 造プログラム
(I n t e r d i s c i p l i n a r y Theoretical and Mathematical Sciences Program, 略称iTHEMS アイテムズ)は、理論科学・数学・計算科学の研究者が分野の枠を越えて基礎研究を推進する新しい国際研究拠点である。
iTHEMS では、「数理」を軸とする分野横断的手法により、宇宙・物質・生命の解明や、社会における基本問題の解決を目指している。
数学、物理学、生物学、計算科学、情報科学など異なる分野の理論研究者が一つ屋根の下に結集し、それぞれの分野のエキスパートが切磋琢磨し、新たな発展生み出せる環境を、物理的にも精神的にも整備する。
基本の旗として、4つの研究セル(極限宇宙、生命進化、数理とAI、新しい幾何学)をトップダウンで与える。
これらの分野の研究者がその間を行き来し、研究者間での共同研究や、他分野の研究を自身の研究に取り入れるなど、柔軟に進められる体制となっている。
分野横断型研究の例として、生物学者・物理学者がセンターを超えて協力した「進化・生体ダイナミクスにおける速度限界不等式の発見」[160, 161]、数学者・生物学者・物理学者が協力した「複雑な化学反応ネットワークを単純化する数理手法の構築」[162, 163]などが挙げられる。
本プロポーザル作成にあたり、表A–1 のとおり有識者に研究内容や推進体制、国内外動向についてインタビューを実施した(実施日時順、敬称略、所属・役職は実施当時)。
6/20(月) 上田 正仁 東京大学大学院理学系研究科教授
7/7(木) 沙川 貴大 東京大学大学院工学系研究科教授
7/11(月) 白石 直人 東京大学大学院総合文化研究科准教授
7/21(木) 田島 裕康 電気通信大学大学院情報理工学研究科助教
11/10(木) 伊藤 創祐 東京大学大学院理学系研究科附属生物普遍性研究機構講師
12/5(月) 高柳 匡 京都大学基礎物理学研究所教授
12/12(月) 宇賀神 知紀 京都大学白眉センター特定助教
12/14(水) 甘利 俊一 帝京大学先端総合研究機構特任教授
本プロポーザル作成にあたり、下記の通り、科学技術未来戦略ワークショップを開催した。詳細についてはワークショップ報告書[164]を参考されたい。
9:00~9:20 「情報熱力学とその周辺」沙川貴大(東京大学)
9:20~9:40 「省エネルギー性の物理と最適輸送・情報幾何の数理」伊藤創祐(東京大学)
付録B 専門用語説明
・AdS/CFT 対応
反ドジッター宇宙に対するホログラフィー原理。
反ドジッター宇宙(AdS) の重力理論は、その端に存在する共形場理論(CFT:Conformal Field Theory) と同一の理論となるという対応関係を表す。
反ドジッター宇宙を円板とすると、円板の外周に共形場理論が位置することになる。
ドジッター宇宙(dS) に対するホログラフィー原理「dS/CFT 対応」の研究も進められており、そこではドジッター宇宙(dS) の重力理論は無限の未来に位置する共形場理論(CFT) に対応づけられる。
*
・エントロピー生成
エントロピー生成とは、系の不可逆性の度合いを表す物理的な量である。
外界である浴とエネルギーや物質をやり取りする系において、エントロピー生成は系そのもののエントロピーの変化と浴のエントロピーの変化を全て足し上げたものであり、この値が常に非負であることがエントロピー増大則として熱力学第二法則の一つの表現として知られている。
エントロピー生成は「熱力学的力(化学ポテンシャル差、温度差、圧力差、電圧差などに起因する駆動力)」と「熱力学流れ(物質、熱、流体、電気などの流れ)」の積でも表され、状態が変化する際には熱力学的力に駆動されて熱力学流れが生じることから、必ずエントロピー生成が生じる。
*
・カルバック・ライブラー情報量
二つの確率分布がどれだけ異なるかを測る情報理論的な量。
「カルバック・ライブラー距離」と呼ばれる場合もあるが、
距離の公理は満たさないため「距離のようなもの」という方が正しい。
確率分布p とq とのカルバック・ライプラー情報量とは、p をq で近似したときにどのくらい情報が失われるかを表す量とも解釈できる。
・共形場理論
空間の角度を変えない共形変換で不変となる場の量子論を共形場理論と呼ぶ。
共形場理論は拡大縮小しても変わらないというスケール対称性をもち、系の臨界点近傍のダイナミクスを記述する理論として物性物理学を中心に広く知られている。
素粒子物理学では弦理論の数学的な基礎づけを与える理論としても知られ、ゲージ理論と重力理論の双対性の研究でも重要な役割を果たす。
・固有状態熱化仮説(Eigenstate Thermalization Hypothesis, ETH)
孤立量子系が時間発展により熱力学的平衡状態に緩和すること(熱平衡化)を説明する機構。
いくつかの量子系では物理量の期待値が平衡統計力学でのミクロカノニカル平均に緩和することが数値計算により確かめられている。
ETH には「強いETH」と「弱いETH」があり、全ての固有状態は熱的な性質を持つということを主張する「強いETH」が成立すると全ての固有状態で物理量の期待値はミクロカノニカル平均と一致する(系は熱平衡化する)。
一方で、熱平衡化しない量子系も知られている。
「弱いETH」が成立する場合には指数関数的に少ない状態だけが熱平衡化せず、ほとんど全ての固有状態は熱的な性質を持つことを主張する。
・仕事
熱力学において、対象とする系と外部との間でやりとりされる力学的なエネルギー。
系と外部との間でやりとりされる熱と仕事についてのエネルギー保存則が熱力学第一法則である。
・シャノン・エントロピー
情報理論において、ある事象がどの程度の情報を持つのかを測る尺度。
その事象がどれほど起こりにくいかを表す尺度ともみなせる。
「シャノン情報量」「情報エントロピー」などとも呼ばれる。
ありふれた事象にはあまり多くの情報は含まれていないが、珍しい事象にはより多くの「情報」が含まれているとする考え方を反映している。
このときの「情報」とは、あくまでその事象の発生確率のみによって決まる量であり、個人や社会における情報の有用性や価値とは無関係である。
例えば、「私が宝くじに当たる」と「誰か別の人が宝くじに当たる」は、前者の方が価値ある情報に感じるが、シャノン・エントロピーで測った情報量は同じである。
・情報幾何学
確率分布の集合からなる空間を考えて、その空間の中に成り立つ幾何学を考える数学の分野。
統計学、機械学習、情報理論など確率分布が主要な役割を果たす分野において用いられ、幾何学的な直観的な理解と新しい方法論を提供している。
・情報熱機関
熱を仕事やエネルギーに変換する機関を「熱機関」と呼ぶことになぞらえて、フィードバック機構などにより情報を仕事やエネルギーに変換する熱機関を「情報熱機関」と呼ぶ。
「マクスウェルのデーモン」をモデル化するシラード・エンジンは効率100% の情報熱機関だと知られ、
平衡熱力学における効率上限を達成する熱機関であるカルノー・サイクルの情報熱力学版とも言える基本的な熱機関である。
・相互情報量
確率論および情報理論において、2 つの確率変数の相互依存の尺度を表す量である。
最も典型的な相互情報量の物理単位はビットであり、2 を底とする対数が使われることが多い。
・テンソルネットワーク
大きなテンソルを網の目のように接続した小さな多数のテンソルからなるテンソル積の縮約として表現したもの。
統計力学で扱う分配関数や量子力学や場の理論での演算子の期待値、量子多体系の波動関数などを表現するのに用いられる。
テンソルネットワークは計算の高効率化のためだけでなく、トポロジカル量子相の特徴づけにも有用だと知られており、量子化学計算や機械学習など様々な分野への応用も期待されている。
・トポロジカル相
秩序パラメータで特徴づけられる従来の相とは異なり、秩序パラメータを持たず系の大域的なトポロジーによって記述される相。
とくに、物質中の電子の波動関数の位相がもつ幾何学的構造で定義されるトポロジカル不変量で特徴づけられる電子相をトポロジカル量子相と呼ぶ。
代表的なトポロジカル相として量子ホール系やトポロジカル超伝導体などが挙げられる。
・熱力学的不確定性関係
熱や仕事(エントロピー生成)と熱力学的な観測量の揺らぎの間にある「熱力学的な状態間の遷移のスピードや精度を上げるためには十分な熱力学的コストが必要」などのトレードオフ関係は、量子力学の不確定性関係になぞらえて「熱力学的不確定性関係」と呼ばれる。
・非平衡統計力学
統計力学は系のミクロな物理法則を元にしてマクロな性質を導き出す。
マクロに見て時間変化しない熱平衡状態についての統計力学は確立されているが、平衡から離れた非平衡状態の統計力学は未完成とされている。
統計力学から熱力学が導出されると表現されることもあるが、「統計力学が熱力学を基礎づけるのではない。熱力学との整合性こそが、統計力学を基礎づけるのである」という言葉もある[165]。
・フィッシャー情報量
観測値から分布のパラメータを最尤法で推定する際に、観測する確率変数Xがパラメータθに関して持つ情報量。
パラメータがθである母集団の従う分布の確率密度関数 f(Xi|θ) をとするとき、対数尤度関数log f(Xi|θ) をθで2 階微分したものの期待値がフィッシャー情報量である。
・ホログラフィ原理
ある宇宙の重力理論がその宇宙の端に仮想的に存在すると考えられる量子物質を表す理論(共形場の理論)と同一であるとする原理。
対応する2つの理論を比べると、重力理論のほうが共形場の理論より1次元高い時空となっており、平面から立体像が浮かび上がるホログラムに似ていることから「ホログラフィ原理」と呼ばれる。
反ドジッター宇宙のホログラフィ原理(AdS/CFT 対応)は様々な形で検証が進められてきているが、より一般の宇宙に対するホログラフィ原理は未解明の部分が多い。
・マクスウェルのデーモン
1867 年にマクスウェルが提唱した思考実験。
箱の中に入っている多数の気体分子の速度を測定し、それに応じて分子を選り分ける「デーモン(悪魔)」がいれば、箱の中の気体のエントロピーを減らし熱力学第二法則を破ることができるように見える(第二種永久機関)。
パラドックスとして長い間多くの物理学者たちの間で議論されてきたが理解は不完全であった。
近年の研究によって、情報量の概念を導入することで、このようなデーモンと熱力学第二法則とを矛盾なく説明できることがわかった。
・ゆらぎの定理
水中のブラウン粒子などのミクロな系は、同じ条件下での実験でも試行ごとに異なる軌跡をたどる。
このようなミクロな系でのゆらぎを詳細に特徴付ける関係式が「ゆらぎの定理」である。
ゆらぎの定理から熱力学第二法則や非平衡状態についての多くの重要な熱力学法則を導出できるため、ゆらぎの定理はミクロな系の非平衡熱力学で最も重要な関係式である。
・ランダウア原理
情報の消去など論理的に非可逆な操作は熱力学的にも非可逆であり、相応する熱力学的エントロピーの増加が必要であることを主張する原理。
情報処理において1 ビットの情報を失うとき、環境での熱力学的エントロピーの上昇は少なくとも1 ビットであり、環境に放出される熱は最低でもk BT log 2 と計算される(k B はボルツマン定数、T は温度)。
この限界値はランダウア限界と呼ばれる。
・量子多体系
量子力学に従う多数の自由度が互いに相互作用しあう物理系。
磁性や超伝導などの物性は多数の電子(がもつ自由度)の相互作用から創発する量子多体現象だといえる。
各自由度の運動は多体の波動関数によって記述されるが、量子多体系の自由度が増えるとハミルトニアンの次元が指数関数的に増大し、その固有状態も指数関数的に大きなサイズのベクトルになるため、基本的には解析的な厳密解は得られない。
人工的な量子多体系である量子シミュレータによる実験的アプローチの研究も進められている。
・量子もつれ(エンタングルメント)
量子系に現れる古典物理学では説明できない量子力学に特有の相関。
構成する個々の部分系の積として表せない複合系の状態を量子もつれ状態と呼ぶ。
量子もつれは量子通信や量子計算に本質的に必要な要素とされる。
エンタングルメント・エントロピーによって量子もつれの強さを測ることができる。
・ワッサースタイン距離
確率分布の間の距離のひとつ。
直感的には、それぞれの分布を堆積した土の山と見なすとき、一つの山を別の山へと移すときにかかる最小のコストがワッサースタイン距離である(このときのコストは、移されるべき土の量と移す距離を掛けた値)。
ワッサースタイン距離は、確率分布を比較するツールとしての最適輸送の特殊ケースとも見なせることから、カルバック・ライブラー情報量に代わる損失関数として、機械学習での応用が試行されている。
この記事が気に入ったらサポートをしてみませんか?
