
【python cvxpy】モデリング言語cvxpyを利用して数理最適化問題を解く
【はじめに】
これまで「数理最適化問題」を解く際に「ソルバーに渡すモデリング言語」として「python-MIP」や「PuLP」の使い方を取り上げてきた。
今回は「モデリング言語:cvxpy」を取り上げる
【cvxpyの特徴について】
「モデリング言語:cvxpy」の特徴を簡単に言うと、
解きたい問題に対して、
できるだけその数式の表現のまま記述できるようになっている
というもの。
早速、例題を通して使い方をざっと見ていく。
【例題】:制約条件付きの最小二乗法(least squares problem with box constraints)
例題には「公式サイトトップにある例」を「もう少し簡単にしたもの」を使ってみる。
【問題】
以下の「3変数を共有する6本の連立方程式」を考える。
すべての方程式を同時に満たすことはできないため、
(x0, x1, x2)の値をいい感じに決めて、「6つの方程式全体」として見たら大きく乖離しないようにしたい。
ただし、求める(x0, x1, x2)の値は0~1の範囲でいい感じに決める。
→ ようは近似式っぽいものを作りたいということ
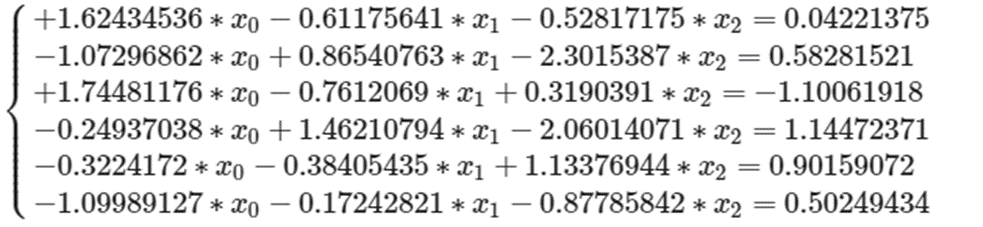
■やりたいことのイメージ図

つまりは、
3つの入力データを投入したら、6つの方程式全体に対して
「当たらずと雖も遠からず(あたらずといえどもとおからず)な近似式」
を作りたいということ。
もっと砕けた言い方をすると、
「6つの方程式から近似式を見つける」→「6回inputデータを投入したらそれぞれ出力されたoutputの結果」をヒントに「それっぽい近似式」を推測してね
ってこと。
※今回作りたい近似式
$${input_0*x_0 + input_1*x_1 + input_2*x_2=output}$$
▲この$${x_0}$$,$${x_1}$$,$${x_2}$$をいい感じに決めたい。
【解答例】
実行環境は「Google Colab」。
【1】cvxpyのインストール
!pip install cvxpy
!pip install --upgrade cvxpy■バージョンや対応ソルバ情報を確認してみる
import cvxpy as cp
# バージョン確認
print(cp.__version__)
# 定義されているソルバーを出力してみる(settings.pyより)
print(cp.settings.SOLVERS)【ここまでの実行結果例】
1.2.0
['ECOS', 'CVXOPT', 'GLOP', 'GLPK', 'GLPK_MI', 'SCS', 'GUROBI', 'OSQP', 'CPLEX', 'MOSEK', 'CBC', 'XPRESS', 'NAG', 'PDLP', 'SCIP', 'SCIPY']
■インストール済みのソルバーを確認する
cvxpyと一緒にインストールされるソルバーを確認してみる
print( cp.installed_solvers() )【ここまでの実行結果例】
['CVXOPT', 'ECOS', 'ECOS_BB', 'GLPK', 'GLPK_MI', 'OSQP', 'SCIPY', 'SCS']
【2】サンプルデータの用意
例題の連立方程式は、次のような行列式で表現することができる。

これをふまえて、A,x,bそれぞれにわけて、必要なサンプルデータを用意する。


■行列Aと行列bのデータを用意
import numpy as np
A = np.array( [
[ 1.62434536, -0.61175641, -0.52817175],
[-1.07296862, 0.86540763, -2.3015387 ],
[ 1.74481176, -0.7612069 , 0.3190391 ],
[-0.24937038, 1.46210794, -2.06014071],
[-0.3224172 , -0.38405435, 1.13376944],
[-1.09989127, -0.17242821, -0.87785842]
])
b = np.array(
[ 0.04221375, 0.58281521, -1.10061918, 1.14472371, 0.90159072, 0.50249434 ]
)【3】変数xの定義
「cvxpy」では「Variable()」をつかって変数を定義する。
n = len(A[0]) # 用意する変数の数
x = cp.Variable(shape=(n,))
print(x)【ここまでの実行結果例】
var213
【4】目的関数
繰り返しになるが今回の問題は
「3変数を共有する6つの方程式すべて」について、できるだけ
左辺 ≒ 右辺
(左辺の値が右辺の値に近くなるようにする)
となるようにする。
※「当たらずと雖も遠からず(あたらずといえどもとおからず)な近似式」を作る
というもの。
これを実現するために
「残差平方和(RSS:residual sum of squares)」を「できるだけ小さくする(0に近づける)」ことを「目的関数」とする。
※残差平方和(RSS:residual sum of squares)のイメージ

▲なお、この考え方の場合、「全体として0に近づけるので、どこかの式に大きく乖離が出てしまう可能性はある」が、今回は気にしない。
■Minimize()とsum_squares()
「cvxpy」では「Minimize()」と「sum_squares()」を組み合わせることで「残差平方和:RSSの最小化」を表現できる。
※Minimize()
※sum_squares()
■目的関数を作成
#objective = cp.Minimize(cp.sum_squares(A @ x - b)) #「@」オペレータ(ver3.5以降)の場合
objective = cp.Minimize(cp.sum_squares(np.matmul(A,x) - b)) # 行列演算
print(objective)【ここまでの実行結果例】
minimize quad_over_lin([[ 1.62434536 -0.61175641 -0.52817175]
[-1.07296862 0.86540763 -2.3015387 ]
[ 1.74481176 -0.7612069 0.3190391 ]
[-0.24937038 1.46210794 -2.06014071]
[-0.3224172 -0.38405435 1.13376944]
[-1.09989127 -0.17242821 -0.87785842]] @ var257 + -[ 0.04221375 0.58281521 -1.10061918 1.14472371 0.90159072 0.50249434], 1.0)
※cvxpyの特徴
この「目的関数」の記述の仕方のように、cvxpyでは数式の記述に近い表現のままプログラムを書けることが特徴の一つである。
※補足:行列の掛け算について
行列の掛け算については
・pythonの「@」オペレータ(ver3.5以降)
・numpy.matmul()
等を使うことができる。
【5】制約条件
今回は
0≤x かつ x≤1 (つまり0~1の範囲の値)
を制約条件として用意してみる。
■制約条件の用意
constraints = [0 <= x, x <= 1]
print(constraints)【実行結果例】
[Inequality(Constant(CONSTANT, ZERO, ())), Inequality(Variable((3,)))]
▲先ほど「定義した変数」に対して、「設定したい制約条件」を記述し「list化」すればよい。
なお、公式ドキュメントにもある通り、
制約条件に比較演算子「>」「<」は使用できない。
かならず「=」をつける必要がある。
【6】「Problemオブジェクト」に「目的関数」と「制約条件」を設定
「cvxpy」では「Problemオブジェクト」に「目的関数」と「制約条件」を設定してsolverに渡すことで、問題を解かせることができる。
※Problemオブジェクト
■Problemオブジェクトに目的関数と制約条件を設定する
prob = cp.Problem(objective, constraints)
print(prob)【ここまでの実行結果例】
minimize quad_over_lin([[ 1.62434536 -0.61175641 -0.52817175]
[-1.07296862 0.86540763 -2.3015387 ]
[ 1.74481176 -0.7612069 0.3190391 ]
[-0.24937038 1.46210794 -2.06014071]
[-0.3224172 -0.38405435 1.13376944]
[-1.09989127 -0.17242821 -0.87785842]] @ var257 + -[ 0.04221375 0.58281521 -1.10061918 1.14472371 0.90159072 0.50249434], 1.0)
subject to 0.0 <= var257
var257 <= 1.0
【7】解を求める
「Problem.solve()」をコールして解を求める。
なお、「cvxpy」はソルバー指定がなければ、数式から裏でいい感じにソルバーを選んで計算をする。
■ソルバーを起動して問題を解く
今回は「verbose=True」として詳細な情報を出力しながら問題を解いている。
prob.solve(verbose=True)【実行結果例】
・・・(略)・・・
OSQP v0.6.2 - Operator Splitting QP Solver
(c) Bartolomeo Stellato, Goran Banjac
University of Oxford - Stanford University 2021
-----------------------------------------------------------------
problem: variables n = 9, constraints m = 12
nnz(P) + nnz(A) = 36
settings: linear system solver = qdldl,
eps_abs = 1.0e-05, eps_rel = 1.0e-05,
eps_prim_inf = 1.0e-04, eps_dual_inf = 1.0e-04,
rho = 1.00e-01 (adaptive),
sigma = 1.00e-06, alpha = 1.60, max_iter = 10000
check_termination: on (interval 25),
scaling: on, scaled_termination: off
warm start: on, polish: on, time_limit: off
・・・(略)・・・
status: solved
solution polish: successful
number of iterations: 50
optimal objective: 2.3010
run time: 6.03e-04s
optimal rho estimate: 2.98e+00
※使用したソルバーや計算結果だけを知りたい場合
# 計算に使用したソルバーを確認
print( prob.solver_stats.solver_name )
# 計算結果を確認
print( prob.status )【ここまでの実行結果例】
OSQP
optimal
▲ status として「optimal」が出力されているので解が計算できている
※「solve()」後に保持している「status」について
「solve()」コール後、計算できたかどうかの結果は「Problem.status」に格納されている。
用意されている「Status」は次の通り。(ver. 1.2.0時点)
OPTIMAL = "optimal"
OPTIMAL_INACCURATE = "optimal_inaccurate"
INFEASIBLE = "infeasible"
INFEASIBLE_INACCURATE = "infeasible_inaccurate"
UNBOUNDED = "unbounded"
UNBOUNDED_INACCURATE = "unbounded_inaccurate"
INFEASIBLE_OR_UNBOUNDED = "infeasible_or_unbounded"
USER_LIMIT = "user_limit"
SOLVER_ERROR = "solver_error"
【8】結果の確認
定義した変数の計算結果は「Variable.value」に格納されている。
■目的関数の最小値:ソルバーが計算した「RSS(残差平方和)」の最小値
print(prob.value)【実行結果例】
2.300981285590133
■定義した変数に対して計算した最適値を出力する
print(x.value)【実行結果例】
[-1.12948270e-21 6.36487459e-01 3.26185025e-22]
▲問題に対する答えとしては
(x1,x2,x3)=(-1.12948270e-21, 6.36487459e-01, 3.26185025e-22)
となる。
つまり、以下のような感じに近似式が見積もられた、ということ。

※おまけ1:近似式に6つの方程式の係数(input相当)の値を入れてみる
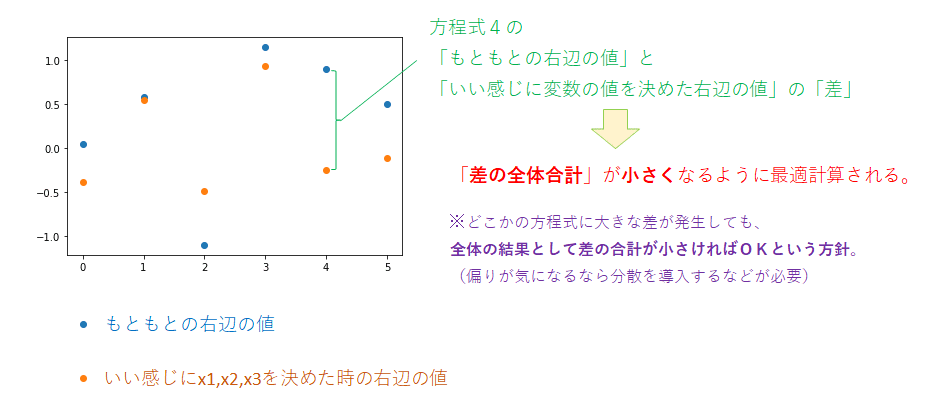
▲見積もられた近似式の計算では、方程式1はもともとの値にも近い結果だが、方程式4は乖離が一番大きい。
しかし、6つの方程式全体としては、乖離(差の合計)が小さくされている。
※特定の方程式だけの差が大きいなど、「偏り」が気になる場合、例えば、『「目的関数」に「分散」を組み込んで調整する』といった方法もある。(より良い手法はその界隈の専門家に聞いてみるのがよい)
※おまけ2:制約条件の充足具合について
今回の制約条件は次の通りであった。
0≤x かつ x≤1 (つまり0~1の範囲の値)
constraints = [0 <= x, x <= 1]
これをふまえると、
「1つ目の変数の計算結果:-1.12948270e-21」は「負の値」なので、計算間違いではないのか?
と疑問に思うかもしれない。
結論からいうと、「制約条件違反」っぽく見えるが、
「誤差の許容範囲にあるので正解扱い」
である。
これは「cvxpy」の「制約条件」の「誤差の許容範囲の精度」をデフォルトで「1e-08(10のマイナス8乗:0.00000001)」としているためである。
※イメージ図

■制約条件の充足具合を確認する
print(prob.constraints[0].value(tolerance= 1e-8)) # 0≦xの制約
print(prob.constraints[1].value()) # x≦1の制約【実行結果例】
True
True
【9】全体コード
最後に全体コードを示しておく。
・実行環境:Google Colab
■インストール
!pip install cvxpy
!pip install --upgrade cvxpy■全体コード
import numpy as np
import cvxpy as cp
# バージョン確認
print(cp.__version__)
# 定義されているソルバーを出力してみる(settings.pyより)
print(cp.settings.SOLVERS)
# インストール済みのソルバの確認
print( cp.installed_solvers() )
A = np.array( [
[ 1.62434536, -0.61175641, -0.52817175],
[-1.07296862, 0.86540763, -2.3015387 ],
[ 1.74481176, -0.7612069 , 0.3190391 ],
[-0.24937038, 1.46210794, -2.06014071],
[-0.3224172 , -0.38405435, 1.13376944],
[-1.09989127, -0.17242821, -0.87785842]
])
b = np.array(
[ 0.04221375, 0.58281521, -1.10061918, 1.14472371, 0.90159072, 0.50249434 ]
)
n = len(A[0]) # 用意する変数の数
x = cp.Variable(shape=(n,))
print(x)
#objective = cp.Minimize(cp.sum_squares(A @ x - b)) #「@」オペレータ(ver3.5以降)の場合
objective = cp.Minimize(cp.sum_squares(np.matmul(A,x) - b)) # 行列演算
print(objective)
constraints = [0 <= x, x <= 1]
print(constraints)
prob = cp.Problem(objective, constraints)
print(prob)
prob.solve(verbose=True)
# 計算に使用したソルバーを確認
print( prob.solver_stats.solver_name )
# 計算結果を確認
print( prob.status ) # status
print(prob.value) # 目的関数の最小値
print(x.value) # 計算により決定された変数の値
# 制約条件の充足状況
print(prob.constraints[0].value(tolerance= 1e-8)) # 0≦xの制約
print(prob.constraints[1].value()) # x≦1の制約【実行結果例】
1.2.0
['ECOS', 'CVXOPT', 'GLOP', 'GLPK', 'GLPK_MI', 'SCS', 'GUROBI', 'OSQP', 'CPLEX', 'MOSEK', 'CBC', 'XPRESS', 'NAG', 'PDLP', 'SCIP', 'SCIPY']
['CVXOPT', 'ECOS', 'ECOS_BB', 'GLPK', 'GLPK_MI', 'OSQP', 'SCIPY', 'SCS']
… (略) …
minimize quad_over_lin([[ 1.62434536 -0.61175641 -0.52817175]
[-1.07296862 0.86540763 -2.3015387 ]
[ 1.74481176 -0.7612069 0.3190391 ]
[-0.24937038 1.46210794 -2.06014071]
[-0.3224172 -0.38405435 1.13376944]
[-1.09989127 -0.17242821 -0.87785842]] @ var257 + -[ 0.04221375 0.58281521 -1.10061918 1.14472371 0.90159072 0.50249434], 1.0)
subject to 0.0 <= var257
var257 <= 1.0
…(略)…
OSQP v0.6.2 - Operator Splitting QP Solver
(c) Bartolomeo Stellato, Goran Banjac
University of Oxford - Stanford University 2021
…(略)…
status: solved
solution polish: successful
number of iterations: 50
optimal objective: 2.3010
run time: 2.44e-04s
optimal rho estimate: 2.98e+00
…(略)…
OSQP
optimal
2.300981285590133
[-1.12948270e-21 6.36487459e-01 3.26185025e-22]
True
True
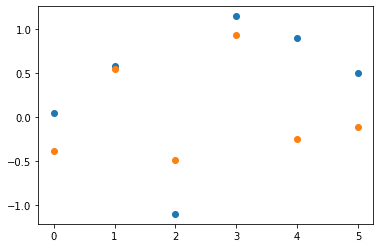
■見積もった近似式に6つの係数(input相当)を入れて可視化するコード
%matplotlib inline
import matplotlib.pyplot as plt
def calc_output(in1, in2, in3):
return x.value[0]*in1+ x.value[1]*in2+ x.value[2]*in3
fig, ax = plt.subplots()
axis_x = np.arange(len(A))
calc_y = [calc_output(*data) for data in A]
ax.scatter(x=axis_x, y = b)
ax.scatter(x=axis_x, y = calc_y)【実行結果例】
いいなと思ったら応援しよう!

