パシネッティ定理の証明：経済を長期的に支配するのは誰？

パシネッティー定理の証明とその拡張、MMTとの関連性を考察してゆきます。

パシネッティー定理もとい独立定理は、ケインズサーカスの一人でありポストケインジアンの基礎を作った経済学者、ルイジ・パシネッティーによって作られた、当時の主流派に代わる所得分配の理論です。

パシネッティー定理は「もし長期的に完全雇用が達成されたなら、それはどのような経済学的帰結をもたらすのか？」という疑問に答えることが出来るモデルです。

この理論は二コラ・カレドアが元々考案していた分配の理論を拡張したものになります。

ですので最初にカレドアのモデルを紹介し、それを拡張することでパシネッティー定理の導出を行います。

「政府債務が有限値に収束する事の証明」との繋がりも考察します。

（わんちゃん後編作るかも）

カレドアの分配理論

まずは、経済主体が民間のみの純粋経済＋古典的な世界を想定しましょう。

公理

経済主体は「利潤獲得層（資本家）」と「賃金獲得層（労働者）」に分けられます。

資本家も労働者も貯蓄を行うと想定します。資本家は利潤から貯蓄し、労働者は賃金から貯蓄する。

労働者は貯蓄をする（＝投資をする）が利潤を獲得せず、資本ストックの蓄積もされないと想定する。（＝労働者は資金提供をしない）

文字の定義

Ｙ=総所得。Ｗ＝賃金。Ｒ＝利潤。Ｓ＝貯蓄。Ｋ＝資本ストック。Ｉ＝投資。

sc=資本家の貯蓄性向。sw＝労働者の貯蓄性向。

R/K=利潤率。R/Y＝利潤シェア割合。Ｉ/K＝成長率。V=資本係数。

国民総所得の定義

マクロ均衡条件の定義

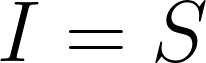
貯蓄の定義

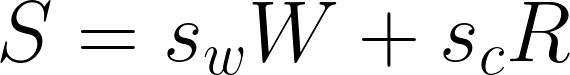
以上三つの方程式体系より、カレドアの分配理論を導出します。

では、マクロ均衡条件と貯蓄の定義式より

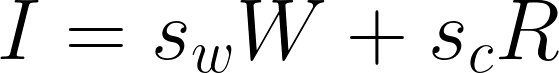
両辺を所得と資本家の貯蓄性向で割ります。

国民総所得の定義式(W=Y-R)より、右辺を利潤シェア割合で括り、式をきれいにしましょう。

では両辺に資本係数（V＝K/Y）の逆数をかけ、利潤率で式を解きます。

終了

さて最後の式が、カレドアが考案した分配の式になります。

利潤率（R/K）は、その時の成長率（I/K）と各経済主体の貯蓄性向で決定され、労働者の貯蓄性向と資本家の貯蓄性向の両方ともが最終的な分配と利潤を決定に影響力を持つ。

「まあ、そりゃそうだろ」って感じですね。

この式についてもっと掘り下げてもよいですが、それはこの記事の目的ではないので、さっさとパシネッティー定理の導出に参りましょう。

パシネッティー定理

パシネッティーは上記のカレドアの式に論理的矛盾がある事を指摘し、これを修正・改良しました。

ます貯蓄が行われるのであれば、それは投資が行われている事と同義ですので、労働者の資本に蓄積がないとおかしいです。

よって「労働者が投資をするが、利潤を獲得しない」という仮定の破棄、労働者も同様に資本をもち、利潤を獲得すると仮定。

これによって、機能的分配と階級的分配をより明確に示せます。

またパシネッティーはこれに続いて「完全雇用が長期的に達成されている」という条件も加えました。

これは「もし超長期的に経済が黄金律を満たし続けたとすれば、その時代の分配は誰が主導権を握るのか？」という問いに答えるためです。

文字の定義

Ｙ=総所得。Ｗ＝賃金。Ｒ＝総利潤、Rｃ＝資本家利潤、Ｒw＝労働者利潤。Ｓ＝総貯蓄，Ｓc＝資本家貯蓄，Ｓw＝労働者貯蓄。Ｋ＝資本ストック，Ｋc＝資本家のストック、Ｋw＝労働者の資本ストック。Ｉ＝投資。

sc=資本家の貯蓄性向。sw＝労働者の貯蓄性向。ｎ＝自然成長率。

R/K=平均利潤率。R/Y＝平均利潤シェア割合。Ｉ/K＝平均成長率。

V＝K/Y=資本係数。

公理

1: マクロ均衡状態にある二部門のみで構成される純粋経済を想定し、完全雇用が常に達成されているとする。

2:資本は、持つ主体に関わらず同じだけの利潤率を稼ぐ

国民総所得の定義

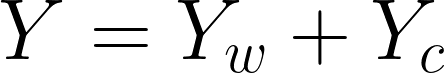
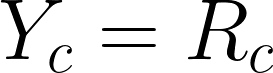
マクロ均衡条件の定義

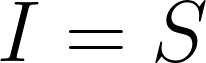
利潤量の定義

貯蓄の定義

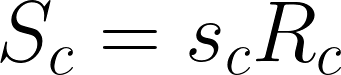
よって

資本ストックの定義

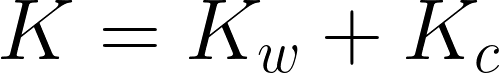
以上、10個の方程式体系から定理の導出をおこなう

定理の証明

貯蓄と国民総所得の定義式より、投資は以下のように書き換えれる。

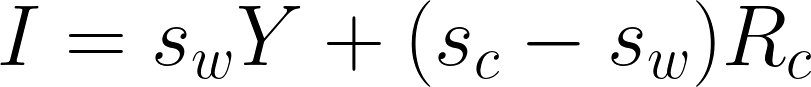
両辺を総所得で割り、資本係数の逆数を掛け、Rc/Yで式を解く

さて、ここまではカレドアの式と非常にそっくりです。

ですが左辺は平均利潤率を表していないため、労働者の総資本分の利潤（Rw/K）を足さなければなりません。

公理①&②より。

黄金時代における資本の成長率は、保持する主体に関わらず常に自然成長率(n)と等しくなり、各主体の資本が稼ぐ利潤も等しいので……(r=R/K)

したがって

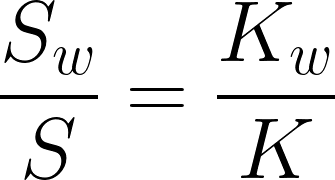
つまり、Pw/Kは以下のようにあらわせれる……

では再度国民所得の定義式と、先ほど求めたRc/Yの式を代入します。

そして上記の式を整理すると……

この式を最初に求めたRc/Kの式に入れて平均利潤率を導出します。

では式全体を利潤率で解きましょう。

「ｎ」は自然成長率「ｒ」は平均利潤率、「ｇ」は平均成長率を意味する

労働者が正の貯蓄性向をもち、資本を所有し、利潤を取得したとしても、完全雇用の世界において利潤率・所得分配を決定するのは資本家である。

よってパシネッティ定理の成立が示された。

考察

さて、カレドアでは労働者の貯蓄性向が０の時のみに成立する関係性が、パシネッティモデルにおいては常に成立します。

「労働者も資本を持ち、利潤を取得し、投資をしているにも拘らず、最終的な分配はすべて資本家が決めてしまう」というパラドックスでした。

この定理は、やはり「長期的完全雇用（＝自然成長率）」と「各主体の利潤率が同値」という仮定に依存しています。

では非現実的な定理か？というわけではありません。

もし長期的にJGPで完全雇用を維持し続ければ、需要が下支えされ、成長率が安定するでしょう。（自然成長率の壁に到達するかは不明）

そうなればパシネッティー定理が成立する可能性は十分にありえます。

MMTとの関連性

また前回の僕の記事「政府債務が有限値に収束する事の証明」を思い出してほしいのですが、あのモデルにおいて「貯蓄性向の上昇」は「政府債務均衡値の上昇」につながりました。

今回のパシネッティ定理において「貯蓄性向の上昇」は「労働者へのより多い分配」につながります。

つまり「より多くの分配を労働者に分けるためには、資本家の貯蓄性向が増える＋政府の債務発行が必要」と結論づける事が出来ます。

これは若干ある意味直観に反する結論かもしれません。

なぜなら資本家の貯蓄性向が増え、それを政府が100％補填するなら。一見それは、金利収入も含めて格差の拡大につながる可能性があるように思えます。

しかし、それが逆にマクロ全体における分配を改善する事につながり、結果的に資本家の資産が増えるとともに、労働者への資産分配＆フローの増加にもつながるわけです。

資本家がより多くの政府債権を持つことが、結果としてマクロ全体の分配化全につながる。ってのは新たなパラドックスかもしれないですねぇ～～

まあ、まだこれは「可能性」のお話ですけどね……

てーことで、パシネッティ定理の証明とMMTとの関連性の考察でした。

もしかしたらパート2するかも……

知らんけど

あーセミナーやだ